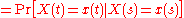Markov process
Encyclopedia
In probability theory
and statistics
, a Markov process, named after the Russian mathematician Andrey Markov
, is a time-varying random phenomenon for which a specific property (the Markov property
) holds. In a common description, a stochastic process
with the Markov property
, or memorylessness, is one for which conditional
on the present state of the system, its future and past are independent.
Markov processes arise in probability and statistics in one of two ways. A stochastic
process, defined via a separate argument, may be shown (mathematically) to have the Markov property
and as a consequence to have the properties that can be deduced from this for all Markov processes. Of more practical importance is the use of the assumption that the Markov property holds for a certain random process in order to construct, ab initio
, a stochastic model for that process. In modelling terms, assuming that the Markov property holds is one of a limited number of simple ways of introducing statistical dependence into a model for a stochastic process in such a way that allows the strength of dependence at different lags to decline as the lag increases.
Often, the term Markov chain
is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain would be defined for a discrete set of times (i.e. a discrete-time Markov Chain) although some authors use the same terminology where "time" can take continuous values. Also see continuous-time Markov process.
es it is simple to formulate the condition specifying whether the Markov property holds while, for others, more sophisticated mathematics is required as described in the article Markov property
. One simple instance relates to a stochastic process
whose states X can take on a discrete set of values. The states vary with time t and hence the values are denoted by X(t). The description here is the same irrespective of whether the time-index is either a continuous variable or a discrete variable. Consider any set of "past times" ( ..., p2, p1), any "present time" s, and any "future time" t, where each of these times is within the range for which the stochastic process is defined, and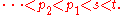
Then the Markov property holds, and the process is a Markov process, if the condition

holds for all sets of values ( ... ,x(p2), x(p1), x(s), x(t) ), and for all sets of times. The interpretation of this is that the conditional probability
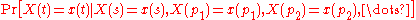
does not depend on any of the past values ( ... ,x(p2), x(p1) ). This captures the idea that the future state is independent of its past states conditionally on the present state (i.e. depends only on the present state).

If Y has the Markov property, then it is a Markovian representation of X. In this case, X is also called a second-order Markov process. Higher-order Markov processes are defined analogously.
An example of a non-Markovian process with a Markovian representation is a moving average time series
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a Markov process, named after the Russian mathematician Andrey Markov
Andrey Markov
Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
, is a time-varying random phenomenon for which a specific property (the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
) holds. In a common description, a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
, or memorylessness, is one for which conditional
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
on the present state of the system, its future and past are independent.
Markov processes arise in probability and statistics in one of two ways. A stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
process, defined via a separate argument, may be shown (mathematically) to have the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
and as a consequence to have the properties that can be deduced from this for all Markov processes. Of more practical importance is the use of the assumption that the Markov property holds for a certain random process in order to construct, ab initio
Ab initio
ab initio is a Latin term used in English, meaning from the beginning.ab initio may also refer to:* Ab Initio , a leading ETL Tool Software Company in the field of Data Warehousing.* ab initio quantum chemistry methods...
, a stochastic model for that process. In modelling terms, assuming that the Markov property holds is one of a limited number of simple ways of introducing statistical dependence into a model for a stochastic process in such a way that allows the strength of dependence at different lags to decline as the lag increases.
Often, the term Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain would be defined for a discrete set of times (i.e. a discrete-time Markov Chain) although some authors use the same terminology where "time" can take continuous values. Also see continuous-time Markov process.
The Markov property
For certain types of stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es it is simple to formulate the condition specifying whether the Markov property holds while, for others, more sophisticated mathematics is required as described in the article Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
. One simple instance relates to a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
whose states X can take on a discrete set of values. The states vary with time t and hence the values are denoted by X(t). The description here is the same irrespective of whether the time-index is either a continuous variable or a discrete variable. Consider any set of "past times" ( ..., p2, p1), any "present time" s, and any "future time" t, where each of these times is within the range for which the stochastic process is defined, and
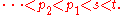
Then the Markov property holds, and the process is a Markov process, if the condition

holds for all sets of values ( ... ,x(p2), x(p1), x(s), x(t) ), and for all sets of times. The interpretation of this is that the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
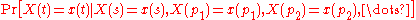
does not depend on any of the past values ( ... ,x(p2), x(p1) ). This captures the idea that the future state is independent of its past states conditionally on the present state (i.e. depends only on the present state).
Markovian representations
In some cases, apparently non-Markovian processes may still have Markovian representations, constructed by expanding the concept of the 'current' and 'future' states. For example, let X be a non-Markovian process. Then define a process Y, such that each state of Y represents a time-interval of states of X. Mathematically, this takes the form:
If Y has the Markov property, then it is a Markovian representation of X. In this case, X is also called a second-order Markov process. Higher-order Markov processes are defined analogously.
An example of a non-Markovian process with a Markovian representation is a moving average time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
.
See also
- Examples of Markov chainsExamples of Markov chains- Board games played with dice :A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. To see the...
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
- Markov decision processMarkov decision processMarkov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
- Dynamics of Markovian particlesDynamics of Markovian ParticlesDynamics of Markovian particles is the basis of a theory for kinetics of particles in open heterogeneous systems. It can be looked upon as an application of the notion of stochastic process conceived as a physical entity; e.g...
- Random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
- Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
- Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
- Markov modelMarkov modelIn probability theory, a Markov model is a stochastic model that assumes the Markov property. Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable.-Introduction:...