
Absorbing Markov chain
Encyclopedia
In the mathematical theory of probability
, an absorbing Markov chain is a Markov chain
in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left.
Like general Markov chains, there can be continuous-time absorbing Markov chains with an infinite state space. However, this article concentrates on the discrete-time discrete-state-space case.
In an absorbing Markov chain, a state that is not absorbing is called transient.
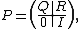
where Q is a t-by-t matrix, R is a nonzero t-by-r matrix, 0 is an r-by-t zero matrix, and I is the r-by-r identity matrix. Thus, Q describes the probability of transitioning from some transient state to another while R describes the probability of transitioning from some transient state to some absorbing state.
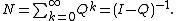
With this matrix in hand, other properties chain are easy to obtain.
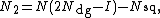
where Ndg is the diagonal matrix
with the same diagonal as N and Nsq is the Hadamard product of N with itself (i.e. each entry of N is squared).
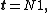
where 1 is a length-t column vector whose entries are all 1.
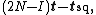
where tsq is the dot product
of t with itself (i.e. each entry of t is squared).
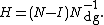
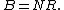
until the sequence (heads, tails, heads) appears. This process is modeled by an absorbing Markov chain with transition matrix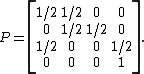
The first state represents the empty string
, the second state the string "H", the third state the string "HT", and the fourth state the string "HTH". Although, the coin flips cease after the string "HTH" is generated, the perspective the absorbing Markov chain is that the process has transitioned into the absorbing state representing the string "HTH" and, therefore, cannot leave.
For this absorbing Markov chain, the fundamental matrix is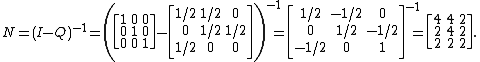
The expected number of steps starting from each of the transient states is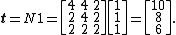
Therefore, the expected number of coin flips before observing the sequence (heads, tails, heads) is 10, the entry for the state representing the empty string.
. The graph on the right plots the probability mass in the lone absorbing state that represents the final square as the transition matrix is raised to larger and larger powers. To determine the expected number of turns to complete the game, compute the vector t as described above and examine tstart, which is approximately 39.2.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, an absorbing Markov chain is a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left.
Like general Markov chains, there can be continuous-time absorbing Markov chains with an infinite state space. However, this article concentrates on the discrete-time discrete-state-space case.
Formal definition
A Markov chain is an absorbing chain if- there is at least one absorbing state and
- it is possible to go from any state to at least one absorbing state in at a finite number of steps.
In an absorbing Markov chain, a state that is not absorbing is called transient.
Canonical form
Let an absorbing Markov chain with transition matrix P have t transient states and r absorbing states. Then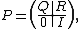
where Q is a t-by-t matrix, R is a nonzero t-by-r matrix, 0 is an r-by-t zero matrix, and I is the r-by-r identity matrix. Thus, Q describes the probability of transitioning from some transient state to another while R describes the probability of transitioning from some transient state to some absorbing state.
Fundamental matrix
A basic property about an absorbing Markov chain is the expected number of visits to a transient state j starting from a transient state i (before being absorbed). The probability of transitioning from i to j in exactly k steps is the (i,j)-entry of Qk. Summing this for all k (from 0 to ∞) yields the desired matrix, called the fundamental matrix and denoted by N. It is easy to prove that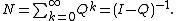
With this matrix in hand, other properties chain are easy to obtain.
Variance on number of visits
The variance on the number of visits to a transient state j with starting at a transient state i (before being absorbed) is the (i,j)-entry of the matrix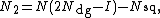
where Ndg is the diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with the same diagonal as N and Nsq is the Hadamard product of N with itself (i.e. each entry of N is squared).
Expected number of steps
The expected number of steps before being absorbed when starting in transient state i is the ith entry of the vector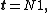
where 1 is a length-t column vector whose entries are all 1.
Variance on number of steps
The variance on the number of steps before being absorbed when starting in transient state i is the ith entry of the vector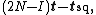
where tsq is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of t with itself (i.e. each entry of t is squared).
Transient probabilities
The probability of visiting transient state j when starting at a transient state i is the (i,j)-entry of the matrix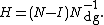
Absorbing probabilities
Another property is the probability of being absorbed in the absorbing state j when starting from transient state i, which is the (i,j)-entry of the matrix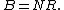
String generation
Consider the process of repeatedly flipping a fair coinFair coin
In probability theory and statistics, a sequence of independent Bernoulli trials with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin...
until the sequence (heads, tails, heads) appears. This process is modeled by an absorbing Markov chain with transition matrix
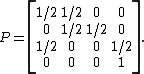
The first state represents the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
, the second state the string "H", the third state the string "HT", and the fourth state the string "HTH". Although, the coin flips cease after the string "HTH" is generated, the perspective the absorbing Markov chain is that the process has transitioned into the absorbing state representing the string "HTH" and, therefore, cannot leave.
For this absorbing Markov chain, the fundamental matrix is
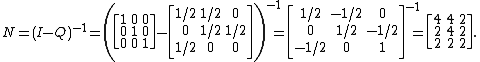
The expected number of steps starting from each of the transient states is
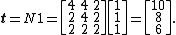
Therefore, the expected number of coin flips before observing the sequence (heads, tails, heads) is 10, the entry for the state representing the empty string.
Games of chance
Games base entirely on chance can be modeled by an absorbing Markov chain. A classic example of this is the ancient Indian board game Snakes and LaddersSnakes and ladders
Snakes and Ladders is an ancient Indian board game regarded today as a worldwide classic. It is played between two or more players on a game board having numbered, gridded squares. A number of "ladders" and "snakes" are pictured on the board, each connecting two specific board squares...
. The graph on the right plots the probability mass in the lone absorbing state that represents the final square as the transition matrix is raised to larger and larger powers. To determine the expected number of turns to complete the game, compute the vector t as described above and examine tstart, which is approximately 39.2.

