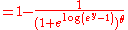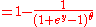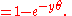Random variable
Encyclopedia
In probability
and statistics
, a random variable or stochastic variable is, roughly speaking, a variable
whose value results from a measurement on some type of random process. Formally, it is a function from a probability space
, typically to the real numbers, which is measurable functionmeasurable. (For finite probability spaces, the measurable requirement is superfluous.) Intuitively, a random variable is a numerical description of the outcome of an experiment (e.g., the possible results of rolling two dice: (1, 1), (1, 2), etc.) Random variables can be classified as either discrete (a random variable that may assume either a finite number of values or an infinite sequence of values) or as continuous (a variable that may assume any numerical value in an interval or collection of intervals).
A random variable's possible values might represent the possible outcomes of a yet-to-be-performed experiment, or the potential values of a quantity whose already-existing value is uncertain (e.g., as a result of incomplete information or imprecise measurements). Intuitively, a random variable can be thought of as a quantity whose value is not fixed, but which can take on different values; a probability distribution
is used to describe the probabilities of different values occurring. Realizations of a random variable are called random variate
s.
Random variables are usually real-valued, but one can consider arbitrary types such as boolean values, complex numbers, vectors, matrices
, sequences
, trees
, sets
, shapes, manifolds, functions
, and processes
. The term random element
is used to encompass all such related concepts. A related concept is the stochastic process
, a set of indexed random variables (typically indexed by time or space).
. In addition to scientific applications, random variables were developed for the analysis of games of chance
and stochastic
events. In such instances, the function that maps the outcome to a real number is often the identity function
or similarly trivial function, and not explicitly described. In many cases, however, it is useful to consider random variables that are functions of other random variables, and then the mapping function included in the definition of a random variable becomes important. As an example, the square of a random variable distributed according to a standard normal distribution is itself a random variable, with a chi-squared distribution. One way to think of this is to imagine generating a large number of samples from a standard normal distribution, squaring each one, and plotting a histogram of the values observed. With enough samples, the graph of the histogram will approximate the density function of a chi-squared distribution with one degree of freedom.
Another example is the sample mean, which is the average of a number of samples. When these samples are independent observations of the same random event they can be called independent identically distributed random variables. Since each sample is a random variable, the sample mean is a function of random variables and hence a random variable itself, whose distribution can be computed and properties determined.
One of the reasons that real-valued random variables are so commonly considered is that the expected value
(a type of average) and variance
(a measure of the "spread", or extent to which the values are dispersed) of the variable can be computed.
There are several types of random variables, the most common two are the discrete and the continuous. A discrete random variable maps outcomes to values of a countable set (e.g., the integer
s), with each value in the range
having probability greater than or equal to zero. A continuous random variable maps outcomes to values of an uncountable set (e.g., the real number
s). For a continuous random variable, the probability of any specific value is zero, whereas the probability of some infinite set of values (such as an interval of non-zero length) may be positive. A random variable can be "mixed", with part of its probability spread out over an interval like a typical continuous variable, and part of it concentrated on particular values like a discrete variable. These classifications are equivalent to the categorization of probability distribution
s.
The expected value of random vectors, random matrices
, and similar aggregates of fixed structure is defined as the aggregation of the expected value computed over each individual element. The concept of "variance of a random vector" is normally expressed through a covariance matrix
. No generally-agreed-upon definition of expected value or variance exists for cases other than just discussed.
 = {heads, tails}. We can introduce a real-valued random variable Y as follows:
= {heads, tails}. We can introduce a real-valued random variable Y as follows:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a random variable or stochastic variable is, roughly speaking, a variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
whose value results from a measurement on some type of random process. Formally, it is a function from a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, typically to the real numbers, which is measurable functionmeasurable. (For finite probability spaces, the measurable requirement is superfluous.) Intuitively, a random variable is a numerical description of the outcome of an experiment (e.g., the possible results of rolling two dice: (1, 1), (1, 2), etc.) Random variables can be classified as either discrete (a random variable that may assume either a finite number of values or an infinite sequence of values) or as continuous (a variable that may assume any numerical value in an interval or collection of intervals).
A random variable's possible values might represent the possible outcomes of a yet-to-be-performed experiment, or the potential values of a quantity whose already-existing value is uncertain (e.g., as a result of incomplete information or imprecise measurements). Intuitively, a random variable can be thought of as a quantity whose value is not fixed, but which can take on different values; a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is used to describe the probabilities of different values occurring. Realizations of a random variable are called random variate
Random variate
A random variate is a particular outcome of a random variable: the random variates which are other outcomes of the same random variable would have different values. Random variates are used when simulating processes driven by random influences...
s.
Random variables are usually real-valued, but one can consider arbitrary types such as boolean values, complex numbers, vectors, matrices
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
, sequences
Random sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...
, trees
Random tree
In mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:...
, sets
Random compact set
In mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.-Definition:...
, shapes, manifolds, functions
Random function
A random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...
, and processes
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. The term random element
Random element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
is used to encompass all such related concepts. A related concept is the stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, a set of indexed random variables (typically indexed by time or space).
Introduction
Real-valued random variables (those whose range is the real numbers) are used in the sciences to make predictions based on data obtained from scientific experimentsExperiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
. In addition to scientific applications, random variables were developed for the analysis of games of chance
Game of chance
A game of chance is a game whose outcome is strongly influenced by some randomizing device, and upon which contestants may or may not wager money or anything of monetary value...
and stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
events. In such instances, the function that maps the outcome to a real number is often the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
or similarly trivial function, and not explicitly described. In many cases, however, it is useful to consider random variables that are functions of other random variables, and then the mapping function included in the definition of a random variable becomes important. As an example, the square of a random variable distributed according to a standard normal distribution is itself a random variable, with a chi-squared distribution. One way to think of this is to imagine generating a large number of samples from a standard normal distribution, squaring each one, and plotting a histogram of the values observed. With enough samples, the graph of the histogram will approximate the density function of a chi-squared distribution with one degree of freedom.
Another example is the sample mean, which is the average of a number of samples. When these samples are independent observations of the same random event they can be called independent identically distributed random variables. Since each sample is a random variable, the sample mean is a function of random variables and hence a random variable itself, whose distribution can be computed and properties determined.
One of the reasons that real-valued random variables are so commonly considered is that the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
(a type of average) and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
(a measure of the "spread", or extent to which the values are dispersed) of the variable can be computed.
There are several types of random variables, the most common two are the discrete and the continuous. A discrete random variable maps outcomes to values of a countable set (e.g., the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s), with each value in the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
having probability greater than or equal to zero. A continuous random variable maps outcomes to values of an uncountable set (e.g., the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). For a continuous random variable, the probability of any specific value is zero, whereas the probability of some infinite set of values (such as an interval of non-zero length) may be positive. A random variable can be "mixed", with part of its probability spread out over an interval like a typical continuous variable, and part of it concentrated on particular values like a discrete variable. These classifications are equivalent to the categorization of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s.
The expected value of random vectors, random matrices
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
, and similar aggregates of fixed structure is defined as the aggregation of the expected value computed over each individual element. The concept of "variance of a random vector" is normally expressed through a covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
. No generally-agreed-upon definition of expected value or variance exists for cases other than just discussed.
Examples
The possible outcomes for one coin toss can be described by the state space = {heads, tails}. We can introduce a real-valued random variable Y as follows:
= {heads, tails}. We can introduce a real-valued random variable Y as follows:
-
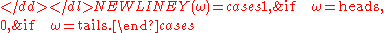
If the coin is equally likely to land on either side then it has a probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
given by:
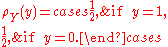
A random variable can also be used to describe the process of rolling a and the possible outcomes. The most obvious representation is to take the set = {1, 2, 3, 4, 5, 6} as the state space, defining the random variable X equal to the number rolled.
= {1, 2, 3, 4, 5, 6} as the state space, defining the random variable X equal to the number rolled.
In this case,


An example of a continuous random variable would be one based on a spinner that can choose a horizontal direction. Then the values taken by the random variable are directions. We could represent these directions by North West, East South East, etc. However, it is commonly more convenient to map the sample space to a random variable which takes values which are real numbers. This can be done, for example, by mapping a direction to a bearing in degrees clockwise from North. The random variable then takes values which are real numbers from the interval [0, 360), with all parts of the range being "equally likely". In this case, X = the angle spun. Any real number has probability zero of being selected, but a positive probability can be assigned to any range of values. For example, the probability of choosing a number in [0, 180] is ½. Instead of speaking of a probability mass function, we say that the probability density of X is 1/360. The probability of a subset of [0, 360) can be calculated by multiplying the measure of the set by 1/360. In general, the probability of a set for a given continuous random variable can be calculated by integrating the density over the given set.
An example of a random variable of mixed type would be based on an experiment where a coin is flipped and the spinner is spun only if the result of the coin toss is heads. If the result is tails, X = −1; otherwise X = the value of the spinner as in the preceding example. There is a probability of ½ that this random variable will have the value −1. Other ranges of values would have half the probability of the last example.
Formal definition
Let be a probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
and a measurable space. Then an random variable is a function which is . The latter means that, for every subset , its preimage where }. This definition enables us to measure any element B in the target space by looking at its preimage, which by assumption is measurable.
When E is a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, then the most common choice for the σ-algebra ℰ is to take it equal to the Borel σ-algebra ℬ(E), which is the σ-algebra generated by the collection of all open sets in E. In such case the random variable is called the random variable. Moreover, when space E is the real line ℝ, then such real-valued random variable is called simply the random variable.
Real-valued random variables
In this case the observation space is the real numbers. Recall,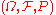 is the probability space. For real observation space, the function
is the probability space. For real observation space, the function  is a real-valued random variable if
is a real-valued random variable if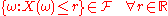
This definition is a special case of the above because generates the Borel sigma-algebra on the real numbers, and it is enough to check measurability on a generating set. (Here we are using the fact that
generates the Borel sigma-algebra on the real numbers, and it is enough to check measurability on a generating set. (Here we are using the fact that 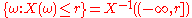 .)
.)
Distribution functions of random variables
Associating a cumulative distribution function (CDF) with a random variable is a generalization of assigning a value to a variable. If the CDF is a (right continuous) Heaviside step functionHeaviside step functionThe Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
then the variable takes on the value at the jump with probability 1. In general, the CDF specifies the probability that the variable takes on particular values.
If a random variable defined on the probability space
defined on the probability space 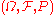 is given, we can ask questions like "How likely is it that the value of
is given, we can ask questions like "How likely is it that the value of  is bigger than 2?". This is the same as the probability of the event
is bigger than 2?". This is the same as the probability of the event 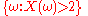 which is often written as
which is often written as 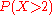 for short, and easily obtained since
for short, and easily obtained since 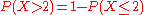
Recording all these probabilities of output ranges of a real-valued random variable X yields the probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of X. The probability distribution "forgets" about the particular probability space used to define X and only records the probabilities of various values of X. Such a probability distribution can always be captured by its cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
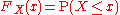
and sometimes also using a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. In measure-theoretic terms, we use the random variable X to "push-forward" the measure P on Ω to a measure dF on R.
The underlying probability space Ω is a technical device used to guarantee the existence of random variables, and sometimes to construct them. In practice, one often disposes of the space Ω altogether and just puts a measure on R that assigns measure 1 to the whole real line, i.e., one works with probability distributions instead of random variables.
Moments
The probability distribution of a random variable is often characterised by a small number of parameters, which also have a practical interpretation. For example, it is often enough to know what its "average value" is. This is captured by the mathematical concept of expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a random variable, denoted E[X], and also called the first momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
. In general, E[f(X)] is not equal to f(E[X]). Once the "average value" is known, one could then ask how far from this average value the values of X typically are, a question that is answered by the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a random variable. E[X] can be viewed intuitively as an average obtained from an infinite population, the members of which are particular evaluations of X.
Mathematically, this is known as the (generalised) problem of moments: for a given class of random variables X, find a collection {fi} of functions such that the expectation values E[fi(X)] fully characterise the distribution of the random variable X.
Functions of random variables
If we have a random variable on
on  and a Borel measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
and a Borel measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
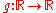 , then
, then 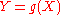 will also be a random variable on
will also be a random variable on  , since the composition of measurable functions is also measurable. (However, this is not true if
, since the composition of measurable functions is also measurable. (However, this is not true if 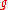 is Lebesgue measurable.) The same procedure that allowed one to go from a probability space
is Lebesgue measurable.) The same procedure that allowed one to go from a probability space 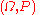 to
to 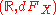 can be used to obtain the distribution of
can be used to obtain the distribution of  . The cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
. The cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of is
is
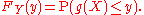
If function g is invertible, i.e. g−1 exists, and increasing, then the previous relation can be extended to obtain
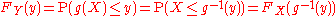
and, again with the same hypotheses of invertibility of g, assuming also differentiability, we can find the relation between the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s by differentiating both sides with respect to y, in order to obtain
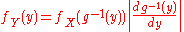 .
.
If there is no invertibility of g but each y admits at most a countable number of roots (i.e. a finite, or countably infinite, number of xi such that y = g(xi)) then the previous relation between the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s can be generalized with
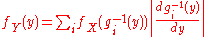
where xi = gi-1(y). The formulas for densities do not demand g to be increasing.
Example 1
Let X be a real-valued, continuous random variable and let Y = X2.
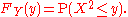
If y < 0, then P(X2 ≤ y) = 0, so
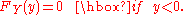
If y ≥ 0, then
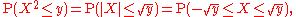
so

Example 2
Suppose is a random variable with a cumulative distribution
is a random variable with a cumulative distribution
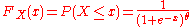
where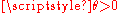 is a fixed parameter. Consider the random variable
is a fixed parameter. Consider the random variable 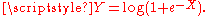 Then,
Then,
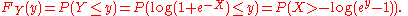
The last expression can be calculated in terms of the cumulative distribution of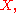 so
so
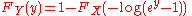
Equivalence of random variables
There are several different senses in which random variables can be considered to be equivalent. Two random variables can be equal, equal almost surely, or equal in distribution.
In increasing order of strength, the precise definition of these notions of equivalence is given below.
Equality in distribution
If the sample space is a subset of the real line a possible definition is that random variables X and Y are equal in distribution if
they have the same distribution functions:
Two random variables having equal moment generating functions have the same distribution. This provides, for example, a useful method of checking equality of certain functions of i.i.d. random variables. However, the moment generating function exists only for distributions that are good enough.
Almost sure equality
Two random variables X and Y are equal almost surely if, and only if, the probability that they are different is zero:
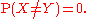
For all practical purposes in probability theory, this notion of equivalence is as strong as actual equality. It is associated to the following distance:

where "ess sup" represents the essential supremum in the sense of measure theory.
Equality
Finally, the two random variables X and Y are equal if they are equal as functions on their measurable space:
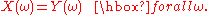
Convergence
A significant theme in mathematical statistics consists of obtaining convergence results for certain sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of random variables; for instance the law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
and the central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
There are various senses in which a sequence (Xn) of random variables can converge to a random variable X. These are explained in the article on convergence of random variablesConvergence of random variablesIn probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
.
Literature
- Kallenberg, O., Random Measures, 4th edition. Academic Press, New York, London; Akademie-Verlag, Berlin (1986). MR0854102 ISBN 0-12-394960-2
- Kallenberg, O., Foundations of Modern Probability, 2nd edition. Springer-Verlag, New York, Berlin, Heidelberg (2001). ISBN 0-387-95313-2
- Papoulis, AthanasiosAthanasios PapoulisAthanasios Papoulis was a Greek-American engineer and applied mathematician.-Life:Papoulis was born in Athens, Greece in 1921 and graduated from National Technical University of Athens...
1965 Probability, Random Variables, and Stochastic Processes. McGraw–Hill Kogakusha, Tokyo, 9th edition, ISBN 0-07-119981-0. - Anderson, Sweeney, Williams, Freeman, Shoesmith. Statistics for Business and Economics - 2nd Edition. Cengage Learning (2010). ISBN 978-1-4080-1810-1
-