Information theory is a branch of applied mathematics

Applied mathematics

Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...

 and electrical engineering

Electrical engineering

Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...

 involving the quantification

Quantification

Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...

 of information

Information

Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...

. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

 operations such as compressing data

Data compression

In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....

 and on reliably storing and communicating

Telecommunication

Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...

 data. Since its inception it has broadened to find applications in many other areas, including statistical inference

Statistical inference

In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...

, natural language processing

Natural language processing

Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....

, cryptography

Cryptography

Cryptography is the practice and study of techniques for secure communication in the presence of third parties...

 generally, networks other than communication networks — as in neurobiology, the evolution and function of molecular codes, model selection in ecology, thermal physics, quantum computing, plagiarism detection and other forms of data analysis

Data analysis

Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...

.

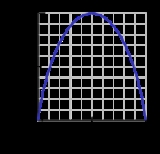
A key measure of information is known as entropy, which is usually expressed by the average number of bits needed to store or communicate one symbol in a message.