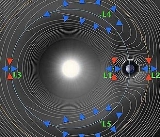
Lagrangian point
Encyclopedia
The Lagrangian points (ləˈɡrɑːndʒiən; also Lagrange points, L-points, or libration
points) are the five positions in an orbit
al configuration where a small object affected only by gravity
can theoretically be stationary relative to two larger objects (such as a satellite
with respect to the Earth
and Moon
). The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force
required to rotate with them.
Lagrangian points are the stationary solutions of the circular restricted three-body problem. For example, given two massive bodies in circular orbit
s around their common center of mass
, there are five positions in space where a third body, of comparatively negligible mass
, could be placed so as to maintain its position relative to the two massive bodies. As seen in a rotating reference frame
with the same period as the two co-orbiting bodies, the gravitational field
s of two massive bodies combined with the satellite's circular motion are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies.
. They are not, in the usual sense, Lagrange Points.
In 1772, the Italian-French mathematician Joseph Louis Lagrange
was working on the famous three-body problem
when he discovered an interesting quirk in the results. Originally, he had set out to discover a way to easily calculate the gravitational interaction between arbitrary numbers of bodies in a system, because Newtonian mechanics
concludes that such a system results in the bodies orbiting chaotically
until there is a collision, or a body is thrown out of the system so that equilibrium
can be achieved.
The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is the relatively simple two-body problem
, with the bodies orbiting around their common center of mass. However, once more than two bodies are introduced, the mathematical calculations become very complicated. It becomes necessary to calculate the gravitational interaction between every pair of objects at every point along its trajectory.
Lagrange, however, wanted to make this simpler. He did so with a simple hypothesis: The trajectory of an object is determined by finding a path that minimizes the action
over time. This is found by subtracting the potential energy
from the kinetic energy
. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics
. With his new system of calculations, Lagrange’s work led him to hypothesize
how a third body of negligible mass would orbit around two larger bodies which were already in a near-circular orbit. In a frame of reference that rotates with the larger bodies, he found five specific fixed points where the third body experiences zero net force as it follows the circular orbit of its host bodies (planets). These points were named “Lagrangian points” in Lagrange's honor. It took over a hundred years before his mathematical theory was validated by the discovery of the Trojan asteroids at the and Lagrange points of the Sun–Jupiter system in 1906.
In the more general case of elliptical
orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian “area”. The Lagrangian points constructed at each point in time, as in the circular case, form stationary elliptical orbits which are similar
to the orbits of the massive bodies. This is due to Newton's second law (Force = Mass times Acceleration, or
), where p = mv (p the momentum
, m the mass, and v the velocity) is invariant
if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.
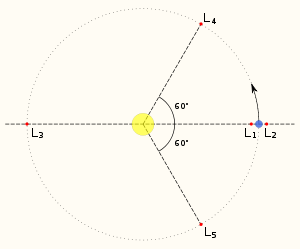The five Lagrangian points are labeled and defined as follows:
The point lies on the line defined by the two large masses M1 and M2, and between them. It is the most intuitively understood of the Lagrangian points: the one where the gravitational attraction of M2 partially cancels M1 gravitational attraction. It is the only L-point which exists in non-rotating systems.
The Sun–Earth is suited for making observations of the Sun. Objects here are never shadowed by the Earth or the Moon. The Solar and Heliospheric Observatory
(SOHO) is stationed in a Halo orbit
at , and the Advanced Composition Explorer
(ACE) is in a Lissajous orbit
, also at the point. WIND is also at L1.
The Earth–Moon allows comparatively easy access to lunar and earth orbits with minimal change in velocity and has this as an advantage to position a half-way manned space station intended to help transport cargo and personnel to the Moon and back.
In a binary star system, the Roche lobe
has its apex located at , if a star overflows its Roche lobe then it will lose matter to its companion star.
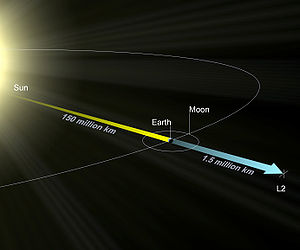The point lies on the line defined by the two large masses, beyond the smaller of the two. Here, the gravitational forces of the two large masses balance the centrifugal effect on a body at .
The Sun–Earth is a good spot for space-based observatories. Because an object around will maintain the same relative position with respect to the Sun and Earth, shielding and calibration are much simpler. It is, however, slightly beyond the reach of Earth's umbra
, so solar radiation is not completely blocked. The Wilkinson Microwave Anisotropy Probe
, Herschel Space Observatory
，Planck space observatory
and Chang'e 2
are already in orbit around the Sun–Earth . The Gaia probe and James Webb Space Telescope
will be placed at the Sun–Earth .
Earth–Moon would be a good location for a communications satellite
covering the Moon's far side.
Earth–Moon would be "an ideal location" for a propellant depot
as part of the proposed Depot-based space transportation architecture.
If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then and are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere
, given by:
where R is the distance between the two bodies.
This distance can be described as being such that the orbital period
, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by
:
The point lies on the line defined by the two large masses, beyond the larger of the two.
The Sun–Earth point was a popular place to put a "Counter-Earth
" in pulp science fiction
and comic book
s. Once space-based observation became possible via satellites and probes, it was shown to hold no such object. The Sun–Earth is unstable and could not contain an object, large or small, for very long. This is because the gravitational forces of the other planets are stronger than that of the Earth (Venus
, for example, comes within 0.3 AU
of this every 20 months). In addition, because Earth's orbit is elliptical and because the barycenter of the Sun–Jupiter system is unbalanced relative to Earth, such a Counter-Earth would frequently be visible from Earth.
A spacecraft orbiting near Sun–Earth would be able to closely monitor the evolution of active sunspot regions before they rotate into a geoeffective position, so that a 7-day early warning could be issued by the NOAA Space Weather Prediction Center. Moreover, a satellite near Sun–Earth would provide very important observations not only for Earth forecasts, but also for deep space support (Mars predictions and for manned mission to near-Earth asteroids). In 2010, spacecraft transfer trajectories to Sun–Earth were studied and several designs were considered.
One example of asteroids which visit an point is the Hilda family
whose orbit brings them to the Sun–Jupiter point.
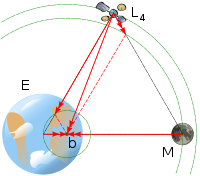The and points lie at the third corners of the two equilateral triangles in the plane of orbit whose common base is the line between the centers of the two masses, such that the point lies behind or ahead of the smaller mass with regard to its orbit around the larger mass.
The reason these points are in balance is that, at and , the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycenter of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycenter in the same ratio
as for the two massive bodies. The barycenter being both the center of mass
and center of rotation of the system, this resultant force is exactly that required to keep a body at the Lagrange point in orbital equilibrium
with the rest of the system. (Indeed, the third body need not have negligible mass). The general triangular configuration was discovered by Lagrange in work on the 3-body problem
.
and are sometimes called triangular Lagrange points or Trojan points. The name Trojan points comes from the Trojan asteroids at the Sun–Jupiter
and points, which themselves are named after characters from Homer
's Iliad
(the legendary siege of Troy
). Asteroids at the point, which leads Jupiter, are referred to as the "Greek camp", while at the point they are referred to as the "Trojan camp". These asteroids are (largely) named after characters from the respective sides of the Trojan War
.
to the line between the two bodies. This can be seen most easily by considering the point. A test mass displaced perpendicularly from the central line would feel a force pulling it back towards the equilibrium point. This is because the lateral components of the two masses' gravity would add to produce this force, whereas the components along the axis between them would balance out. However, if an object located at the point drifted closer to one of the masses, the gravitational attraction it felt from that mass would be greater, and it would be pulled closer. (The pattern is very similar to that of tidal force
s.)
Although the , , and points are nominally unstable, it turns out that it is possible to find stable periodic orbits around these points, at least in the restricted three-body problem. These perfectly periodic orbits, referred to as "halo" orbits
, do not exist in a full n-body dynamical system such as the Solar System
. However, quasi-periodic (i.e., bounded but not precisely repeating) orbits following Lissajous-curve
trajectories do exist in the n-body system. These quasi-periodic Lissajous orbit
s are what most of Lagrangian-point missions to date have used. Although they are not perfectly stable, a relatively modest effort at station keeping can allow a spacecraft to stay in a desired Lissajous orbit for an extended period of time. It also turns out that, at least in the case of Sun–Earth- missions, it is actually preferable to place the spacecraft in a large-amplitude (100000 –) Lissajous orbit, instead of having it sit at the Lagrangian point, because this keeps the spacecraft off the direct Sun–Earth line, thereby reducing the impact of solar interference on Earth–spacecraft communications. Another interesting and useful property of the collinear Lagrangian points and their associated Lissajous orbits is that they serve as "gateways" to control the chaotic trajectories of the Interplanetary Transport Network
.
In contrast to the collinear Lagrangian points, the triangular points ( and ) are stable equilibria (cf. attractor
), provided that the ratio of M1/M2 is greater than 24.96.Actually
This is the case for the Sun–Earth system, the Sun–Jupiter system, and, by a smaller margin, the Earth–Moon system. When a body at these points is perturbed, it moves away from the point, but the factor opposite of that which is increased or decreased by the perturbation (either gravity or angular momentum-induced speed) will also increase or decrease, bending the object's path into a stable, kidney-bean-shaped orbit around the point (as seen in the rotating frame of reference). However, in the Earth–Moon case, the problem of stability is greatly complicated by the appreciable solar gravitational influence.
Lagrangian points through only exist in rotating systems, such as in the monthly orbiting of the Moon about the Earth. At these points, the combined attraction from the two masses is equivalent to what would be exerted by a single mass at the barycenter
of the system, sufficient to cause a small body to orbit with the same period.
Imagine a person spinning a stone at the end of a string. The string provides a tension force that continuously accelerates the stone toward the center. To an ant standing on the stone, however, it seems as if there is an opposite force trying to fling it directly away from the center. This apparent force
is called the centrifugal force. It is actually simply the outward radial component of the stone's inertia caused by its spinning. This same effect is present at the Lagrangian points in the Earth–Moon system, where the analogue of the string is the summed (or net) gravitational attraction of the two masses, and the stone is an asteroid or a spacecraft. The Earth–Moon system and the spacecraft all rotate about this combined center of mass, or barycenter. Because the Earth is much heavier than the Moon, the barycenter is located within the Earth (about 1700 km (1,056.3 mi) below the surface). Any object gravitationally held by the rotating Earth–Moon system will be attracted to the barycenter to an equal and opposite degree as its tendency to fly off into space.
Unlike the other Lagrangian points, would exist even in a non-rotating (static or inertial
) system. In a rotating system, is a bit farther from the (less massive) Moon and closer to the (more massive) Earth than it would be in a non-rotating system. is slightly unstable (see stability, above) because drifting towards the Moon or Earth increases one gravitational attraction while decreasing the other, causing more drift.
At Lagrangian points , , , and , a spacecraft's inertia to move away from the barycenter is balanced by the attraction of gravity toward the barycenter. and are slightly unstable because small changes in position upset the balance between gravity and inertia, allowing one or the other force to dominate, so that the spacecraft either flies off into space or spirals in toward the barycenter. Stability at and is explained by gravitational equilibrium: if the object were moved into a tighter orbit, it would orbit faster which would counteract the increase in gravity; if the object moves into a wider orbit, the gravity is lower, but it loses speed. The net result is that the object appears constantly to hover or orbit around the or point.
The easiest way to understand the resulting stability is to say , , and positions are as stable as a ball balanced on the tip of a wedge would be stable: any disturbance will toss it out of equilibrium. The , and positions are stable as a ball at the bottom of a bowl would be stable: small perturbations will move it out of place, but it will drift back toward the center of the bowl.
Note that from the perspective of the smaller-mass object — from the moon, in the preceding example — a spacecraft might appear to orbit in an irregular path about the or point, but from the perspective above the orbital plane, it becomes clear that both the smaller mass and the spacecraft are orbiting the larger mass (or more precisely, all of the objects are in orbit around the barycenter of the system); they simply have overlapping orbital paths. This point of view difference is illustrated clearly by animations in the 3753 Cruithne and Coriolis effect
articles.
system several thousand asteroid
s, collectively referred to as Trojan asteroids, are in orbits around the Sun–Jupiter and points. Recent observations suggest that the Sun–Neptune
and points, known as the Neptune Trojans
, may be very thickly populated, containing large bodies an order of magnitude more numerous than the Jupiter Trojans. Mars
has four known co-orbital asteroids (5261 Eureka
, , , and ), all at the Lagrangian points. There is one known Trojan for Earth as of July 2011. Clouds of dust, called Kordylewski cloud
s, even fainter than the notoriously weak gegenschein
, may also be present in the and of the Earth–Moon
system.
The Saturnian moon Tethys
has two smaller moons in its and points, Telesto
and Calypso
. The Saturnian moon Dione
also has two Lagrangian co-orbitals, Helene
at its point and Polydeuces
at . The moons wander azimuthally about the Lagrangian points, with Polydeuces describing the largest deviations, moving up to 32 degrees away from the Saturn–Dione point. Tethys and Dione are hundreds of times more massive than their "escorts" (see the moons' articles for exact diameter figures; masses are not known in several cases), and Saturn is far more massive still, which makes the overall system stable.
is the first found Earth Trojan asteroid. It was discovered by the Wide-field Infrared Survey Explorer in October, 2010. After evaluation of the collected data the Trojan character of its motion was published in July 2011. 2010 TK7 has a diameter of 300 meters. Its path is around the Sun–Earth L4 Lagrangian point.
The Earth's companion object 3753 Cruithne
is in a relationship with the Earth which is somewhat Trojan-like, but different from a true Trojan. This asteroid occupies one of two regular solar orbits, one of them slightly smaller and faster than the Earth's orbit, and the other slightly larger and slower. The asteroid periodically alternates between these two orbits due to close encounters with Earth. When the asteroid is in the smaller, faster orbit and approaches the Earth, it gains orbital energy from the Earth and moves up into the larger, slower orbit. It then falls farther and farther behind the Earth, and eventually Earth approaches it from the other direction. Then the asteroid gives up orbital energy to the Earth, and drops back into the smaller orbit, thus beginning the cycle anew. The cycle has no noticeable impact on the length of the year, because Earth's mass is over 20 billion
times more than 3753 Cruithne.
Epimetheus
and Janus
, satellites of Saturn, have a similar relationship, though they are of similar masses and so actually exchange orbits with each other periodically. (Janus is roughly 4 times more massive but still light enough for its orbit to be altered.) Another similar configuration is known as orbital resonance
, in which orbiting bodies tend to have periods of a simple integer ratio
, due to their interaction.
Libration
In astronomy, libration is an oscillating motion of orbiting bodies relative to each other, notably including the motion of the Moon relative to Earth, or of Trojan asteroids relative to planets.-Lunar libration:...
points) are the five positions in an orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
al configuration where a small object affected only by gravity
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
can theoretically be stationary relative to two larger objects (such as a satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
with respect to the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
). The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
required to rotate with them.
Lagrangian points are the stationary solutions of the circular restricted three-body problem. For example, given two massive bodies in circular orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s around their common center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
, there are five positions in space where a third body, of comparatively negligible mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, could be placed so as to maintain its position relative to the two massive bodies. As seen in a rotating reference frame
Rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
with the same period as the two co-orbiting bodies, the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
s of two massive bodies combined with the satellite's circular motion are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies.
History and concepts
Three non-rotating collinear points were discovered by Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. They are not, in the usual sense, Lagrange Points.
In 1772, the Italian-French mathematician Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
was working on the famous three-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
when he discovered an interesting quirk in the results. Originally, he had set out to discover a way to easily calculate the gravitational interaction between arbitrary numbers of bodies in a system, because Newtonian mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
concludes that such a system results in the bodies orbiting chaotically
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
until there is a collision, or a body is thrown out of the system so that equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
can be achieved.
The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is the relatively simple two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
, with the bodies orbiting around their common center of mass. However, once more than two bodies are introduced, the mathematical calculations become very complicated. It becomes necessary to calculate the gravitational interaction between every pair of objects at every point along its trajectory.
Lagrange, however, wanted to make this simpler. He did so with a simple hypothesis: The trajectory of an object is determined by finding a path that minimizes the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
over time. This is found by subtracting the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
from the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. With his new system of calculations, Lagrange’s work led him to hypothesize
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
how a third body of negligible mass would orbit around two larger bodies which were already in a near-circular orbit. In a frame of reference that rotates with the larger bodies, he found five specific fixed points where the third body experiences zero net force as it follows the circular orbit of its host bodies (planets). These points were named “Lagrangian points” in Lagrange's honor. It took over a hundred years before his mathematical theory was validated by the discovery of the Trojan asteroids at the and Lagrange points of the Sun–Jupiter system in 1906.
In the more general case of elliptical
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian “area”. The Lagrangian points constructed at each point in time, as in the circular case, form stationary elliptical orbits which are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to the orbits of the massive bodies. This is due to Newton's second law (Force = Mass times Acceleration, or
), where p = mv (p the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, m the mass, and v the velocity) is invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.
The Lagrangian points
The point lies on the line defined by the two large masses M1 and M2, and between them. It is the most intuitively understood of the Lagrangian points: the one where the gravitational attraction of M2 partially cancels M1 gravitational attraction. It is the only L-point which exists in non-rotating systems.
- Example: An object which orbitOrbitIn physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
more closely than the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
would normally have a shorter orbital period than the Earth, but that ignores the effect of the Earth's own gravitational pull. If the object is directly between the Earth and the Sun, then the Earth's gravity weakens the force pulling the object towards the Sun, and therefore increases the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the point, the orbital period of the object becomes exactly equal to the Earth's orbital period. is about 1.5 million kilometers from the Earth.
The Sun–Earth is suited for making observations of the Sun. Objects here are never shadowed by the Earth or the Moon. The Solar and Heliospheric Observatory
Solar and Heliospheric Observatory
The Solar and Heliospheric Observatory is a spacecraft built by a European industrial consortium led by Matra Marconi Space that was launched on a Lockheed Martin Atlas IIAS launch vehicle on December 2, 1995 to study the Sun, and has discovered over 2100 comets. It began normal operations in May...
(SOHO) is stationed in a Halo orbit
Halo orbit
A halo orbit is a periodic, three-dimensional orbit near the , , or Lagrange points in the three-body problem of orbital mechanics. A spacecraft in a halo orbit does not technically orbit the Lagrange point itself , but travels in a closed, repeating path near the Lagrange point...
at , and the Advanced Composition Explorer
Advanced Composition Explorer
Advanced Composition Explorer is a NASA space exploration mission being conducted as part of the Explorer program to study matter in situ, comprising energetic particles from the solar wind, the interplanetary medium, and other sources. Real-time data from ACE is used by the Space Weather...
(ACE) is in a Lissajous orbit
Lissajous orbit
In orbital mechanics, a Lissajous orbit, , named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbits around a libration point are curved paths that lie...
, also at the point. WIND is also at L1.
The Earth–Moon allows comparatively easy access to lunar and earth orbits with minimal change in velocity and has this as an advantage to position a half-way manned space station intended to help transport cargo and personnel to the Moon and back.
In a binary star system, the Roche lobe
Roche lobe
The Roche lobe is the region of space around a star in a binary system within which orbiting material is gravitationally bound to that star. If the star expands past its Roche lobe, then the material can escape the gravitational pull of the star. If the star is in a binary system then the material...
has its apex located at , if a star overflows its Roche lobe then it will lose matter to its companion star.
- Example: On the side of the Earth away from the Sun, the orbital period of an object would normally be greater than that of the Earth. The extra pull of the Earth's gravity decreases the orbital period of the object, and at the point that orbital period becomes equal to the Earth's.
The Sun–Earth is a good spot for space-based observatories. Because an object around will maintain the same relative position with respect to the Sun and Earth, shielding and calibration are much simpler. It is, however, slightly beyond the reach of Earth's umbra
Umbra
The umbra, penumbra and antumbra are the names given to three distinct parts of a shadow, created by any light source. For a point source only the umbra is cast.These names are most often used to refer to the shadows cast by celestial bodies....
, so solar radiation is not completely blocked. The Wilkinson Microwave Anisotropy Probe
Wilkinson Microwave Anisotropy Probe
The Wilkinson Microwave Anisotropy Probe — also known as the Microwave Anisotropy Probe , and Explorer 80 — is a spacecraft which measures differences in the temperature of the Big Bang's remnant radiant heat — the Cosmic Microwave Background Radiation — across the full sky. Headed by Professor...
, Herschel Space Observatory
Herschel Space Observatory
The Herschel Space Observatory is a European Space Agency space observatory sensitive to the far infrared and submillimetre wavebands. It is the largest space telescope ever launched, carrying a single mirror of in diameter....
，Planck space observatory
Space observatory
A space observatory is any instrument in outer space which is used for observation of distant planets, galaxies, and other outer space objects...
and Chang'e 2
Chang'e 2
Chang'e 2 is a Chinese unmanned lunar probe that was launched on 1 October 2010. It was a follow-up to the Chang'e 1 lunar probe, which was launched in 2007. Chang'e 2 was part of the first phase of the Chinese Lunar Exploration Program, and conducted research from a 100-kilometer-high lunar orbit...
are already in orbit around the Sun–Earth . The Gaia probe and James Webb Space Telescope
James Webb Space Telescope
The James Webb Space Telescope , previously known as Next Generation Space Telescope , is a planned next-generation space telescope, optimized for observations in the infrared. The main technical features are a large and very cold 6.5 meter diameter mirror, an observing position far from Earth,...
will be placed at the Sun–Earth .
Earth–Moon would be a good location for a communications satellite
Communications satellite
A communications satellite is an artificial satellite stationed in space for the purpose of telecommunications...
covering the Moon's far side.
Earth–Moon would be "an ideal location" for a propellant depot
Propellant depot
An orbital propellant depot is a cache of propellant that is placed on an orbit about the Earth or another body to allow spacecraft to be fuelled in space. Launching a spacecraft separately from some of its propellant enables missions with more massive payloads...
as part of the proposed Depot-based space transportation architecture.
If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then and are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere
Hill sphere
An astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own...
, given by:
where R is the distance between the two bodies.
This distance can be described as being such that the orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by
:
Examples
- SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
: 1500000 km (932,059.1 mi) from the Earth - EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and MoonMoonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
: 60000 km (37,282.4 mi) from the Moon
The point lies on the line defined by the two large masses, beyond the larger of the two.
- Example: in the Sun–Earth system exists on the opposite side of the Sun, a little outside the Earth's orbit but slightly closer to the Sun than the Earth is. (This apparent contradiction is because the Sun is also affected by the Earth's gravity, and so orbits around the two bodies' barycenter, which is however well inside the body of the Sun.) At the point, the combined pull of the Earth and Sun again causes the object to orbit with the same period as the Earth.
The Sun–Earth point was a popular place to put a "Counter-Earth
Counter-Earth
The Counter-Earth is a hypothetical body of the Solar system first hypothesized by the presocratic philosopher Philolaus to support his non-geocentric cosmology, in which all objects in the universe revolve around a Central Fire...
" in pulp science fiction
Science fiction
Science fiction is a genre of fiction dealing with imaginary but more or less plausible content such as future settings, futuristic science and technology, space travel, aliens, and paranormal abilities...
and comic book
Comic book
A comic book or comicbook is a magazine made up of comics, narrative artwork in the form of separate panels that represent individual scenes, often accompanied by dialog as well as including...
s. Once space-based observation became possible via satellites and probes, it was shown to hold no such object. The Sun–Earth is unstable and could not contain an object, large or small, for very long. This is because the gravitational forces of the other planets are stronger than that of the Earth (Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
, for example, comes within 0.3 AU
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
of this every 20 months). In addition, because Earth's orbit is elliptical and because the barycenter of the Sun–Jupiter system is unbalanced relative to Earth, such a Counter-Earth would frequently be visible from Earth.
A spacecraft orbiting near Sun–Earth would be able to closely monitor the evolution of active sunspot regions before they rotate into a geoeffective position, so that a 7-day early warning could be issued by the NOAA Space Weather Prediction Center. Moreover, a satellite near Sun–Earth would provide very important observations not only for Earth forecasts, but also for deep space support (Mars predictions and for manned mission to near-Earth asteroids). In 2010, spacecraft transfer trajectories to Sun–Earth were studied and several designs were considered.
One example of asteroids which visit an point is the Hilda family
Hilda family
The Hilda asteroids consists of asteroids with a semi-major axis between 3.7 AU and 4.2 AU, an eccentricity less than 0.3, and an inclination less than 20°. They do not form a true asteroid family, in the sense that they do not descend from a common parent object. Instead, this is a dynamical...
whose orbit brings them to the Sun–Jupiter point.
and
The reason these points are in balance is that, at and , the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycenter of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycenter in the same ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
as for the two massive bodies. The barycenter being both the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
and center of rotation of the system, this resultant force is exactly that required to keep a body at the Lagrange point in orbital equilibrium
Dynamic equilibrium
A dynamic equilibrium exists once a reversible reaction ceases to change its ratio of reactants/products, but substances move between the chemicals at an equal rate, meaning there is no net change. It is a particular example of a system in a steady state...
with the rest of the system. (Indeed, the third body need not have negligible mass). The general triangular configuration was discovered by Lagrange in work on the 3-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
.
and are sometimes called triangular Lagrange points or Trojan points. The name Trojan points comes from the Trojan asteroids at the Sun–Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
and points, which themselves are named after characters from Homer
Homer
In the Western classical tradition Homer , is the author of the Iliad and the Odyssey, and is revered as the greatest ancient Greek epic poet. These epics lie at the beginning of the Western canon of literature, and have had an enormous influence on the history of literature.When he lived is...
's Iliad
Iliad
The Iliad is an epic poem in dactylic hexameters, traditionally attributed to Homer. Set during the Trojan War, the ten-year siege of the city of Troy by a coalition of Greek states, it tells of the battles and events during the weeks of a quarrel between King Agamemnon and the warrior Achilles...
(the legendary siege of Troy
Trojan War
In Greek mythology, the Trojan War was waged against the city of Troy by the Achaeans after Paris of Troy took Helen from her husband Menelaus, the king of Sparta. The war is among the most important events in Greek mythology and was narrated in many works of Greek literature, including the Iliad...
). Asteroids at the point, which leads Jupiter, are referred to as the "Greek camp", while at the point they are referred to as the "Trojan camp". These asteroids are (largely) named after characters from the respective sides of the Trojan War
Trojan War
In Greek mythology, the Trojan War was waged against the city of Troy by the Achaeans after Paris of Troy took Helen from her husband Menelaus, the king of Sparta. The war is among the most important events in Greek mythology and was narrated in many works of Greek literature, including the Iliad...
.
Examples
- The Sun–Earth and points lie 60° ahead of and 60° behind the Earth as it orbits the Sun. The region around these points contain interplanetary dust and at least one asteroid, '2010 TK72010 TK72010 TK7 is the first Earth trojan asteroid to be discovered; it precedes Earth in its orbit around the Sun. Trojan objects are most easily conceived as orbiting at a Lagrangian point, a dynamically stable location 60 degrees ahead of or behind a massive orbiting body, in a type of 1:1 orbital...
' detected October 2010 by WISEWide-field Infrared Survey ExplorerWide-field Infrared Survey Explorer is a NASA infrared-wavelength astronomical space telescope launched on December 14, 2009, and decommissioned/hibernated on February 17, 2011 when its transmitter was turned off...
and announced July 2011. Watch NASAs animated clip.. - The Earth–Moon and points lie 60° ahead of and 60° behind the Moon as it orbits the Earth. They may contain interplanetary dust in what is called Kordylewski cloudKordylewski cloudKordylewski clouds are large concentrations of dust that may exist at the and Lagrangian points of the Earth–Moon system. They were first reported by Polish astronomer Kazimierz Kordylewski in the 1960s, but there is still controversy as to whether they actually exist, due to their extreme...
s. - The region around the Sun–JupiterJupiterJupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
and points are occupied by the Trojan asteroids. - The region around the Sun–NeptuneNeptuneNeptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times...
and points have TrojanNeptune TrojanNeptune trojans are Kuiper belt object-like bodies in solar orbit that have the same orbital period as Neptune and follow roughly the same orbital path...
objects. - SaturnSaturnSaturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
's moon TethysTethys (moon)Tethys or Saturn III is a mid-sized moon of Saturn about across. It was discovered by G. D. Cassini in 1684 and is named after titan Tethys of Greek mythology. Tethys is pronounced |Odysseus]] is about 400 km in diameter, while the largest graben—Ithaca Chasma is about 100 km wide and...
has two much smaller satellites at its and points named TelestoTelesto (moon)Telesto is a moon of Saturn. It was discovered by Smith, Reitsema, Larson and Fountain in 1980 from ground-based observations, and was provisionally designated '. In the following months, several other apparitions were observed: , , and ....
and CalypsoCalypso (moon)Calypso is a moon of Saturn. It was discovered in 1980, from ground-based observations, by Dan Pascu, P. Kenneth Seidelmann, William A. Baum, and Douglas G. Currie, and was provisionally designated ' . Several other apparitions of it were recorded in the following months: , , , and...
, respectively. - Saturn's moon DioneDione (moon)Dione is a moon of Saturn discovered by Cassini in 1684. It is named after the titan Dione of Greek mythology. It is also designated Saturn IV.- Name :...
has smaller moons HeleneHelene (moon)Helene is a moon of Saturn. It was discovered by Pierre Laques and Jean Lecacheux in 1980 from ground-based observations at Pic du Midi Observatory, and was designated . In 1988 it was officially named after Helen of Troy, who was the granddaughter of Cronus in Greek mythology...
and PolydeucesPolydeuces (moon)Polydeuces is a very small natural satellite of Saturn that is co-orbital with Dione and librates around the trailing Lagrangian point . Its diameter is estimated to be about 3.5 km....
at its and points, respectively. - One version of the giant impact hypothesisGiant impact hypothesisThe giant impact hypothesis states that the Moon was created out of the debris left over from a collision between the young Earth and a Mars-sized body. The colliding body is sometimes called Theia for the mythical Greek Titan who was the mother of Selene, the goddess of the moon.The giant impact...
suggests that an object named Theia formed at the Sun–Earth or points and crashed into the Earth after its orbit destabilized, forming the Moon.
Stability
The first three Lagrangian points are technically stable only in the plane perpendicularPerpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the line between the two bodies. This can be seen most easily by considering the point. A test mass displaced perpendicularly from the central line would feel a force pulling it back towards the equilibrium point. This is because the lateral components of the two masses' gravity would add to produce this force, whereas the components along the axis between them would balance out. However, if an object located at the point drifted closer to one of the masses, the gravitational attraction it felt from that mass would be greater, and it would be pulled closer. (The pattern is very similar to that of tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
s.)
Although the , , and points are nominally unstable, it turns out that it is possible to find stable periodic orbits around these points, at least in the restricted three-body problem. These perfectly periodic orbits, referred to as "halo" orbits
Halo orbit
A halo orbit is a periodic, three-dimensional orbit near the , , or Lagrange points in the three-body problem of orbital mechanics. A spacecraft in a halo orbit does not technically orbit the Lagrange point itself , but travels in a closed, repeating path near the Lagrange point...
, do not exist in a full n-body dynamical system such as the Solar System
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
. However, quasi-periodic (i.e., bounded but not precisely repeating) orbits following Lissajous-curve
Lissajous curve
In mathematics, a Lissajous curve , also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equationswhich describe complex harmonic motion...
trajectories do exist in the n-body system. These quasi-periodic Lissajous orbit
Lissajous orbit
In orbital mechanics, a Lissajous orbit, , named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbits around a libration point are curved paths that lie...
s are what most of Lagrangian-point missions to date have used. Although they are not perfectly stable, a relatively modest effort at station keeping can allow a spacecraft to stay in a desired Lissajous orbit for an extended period of time. It also turns out that, at least in the case of Sun–Earth- missions, it is actually preferable to place the spacecraft in a large-amplitude (100000 –) Lissajous orbit, instead of having it sit at the Lagrangian point, because this keeps the spacecraft off the direct Sun–Earth line, thereby reducing the impact of solar interference on Earth–spacecraft communications. Another interesting and useful property of the collinear Lagrangian points and their associated Lissajous orbits is that they serve as "gateways" to control the chaotic trajectories of the Interplanetary Transport Network
Interplanetary Transport Network
The Interplanetary Transport Network is a collection of gravitationally determined pathways through the solar system that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space are redirected using little...
.
In contrast to the collinear Lagrangian points, the triangular points ( and ) are stable equilibria (cf. attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
), provided that the ratio of M1/M2 is greater than 24.96.Actually
This is the case for the Sun–Earth system, the Sun–Jupiter system, and, by a smaller margin, the Earth–Moon system. When a body at these points is perturbed, it moves away from the point, but the factor opposite of that which is increased or decreased by the perturbation (either gravity or angular momentum-induced speed) will also increase or decrease, bending the object's path into a stable, kidney-bean-shaped orbit around the point (as seen in the rotating frame of reference). However, in the Earth–Moon case, the problem of stability is greatly complicated by the appreciable solar gravitational influence.Intuitive explanation
Lagrangian points can be explained intuitively using the Earth–Moon system.Lagrangian points through only exist in rotating systems, such as in the monthly orbiting of the Moon about the Earth. At these points, the combined attraction from the two masses is equivalent to what would be exerted by a single mass at the barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
of the system, sufficient to cause a small body to orbit with the same period.
Imagine a person spinning a stone at the end of a string. The string provides a tension force that continuously accelerates the stone toward the center. To an ant standing on the stone, however, it seems as if there is an opposite force trying to fling it directly away from the center. This apparent force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
is called the centrifugal force. It is actually simply the outward radial component of the stone's inertia caused by its spinning. This same effect is present at the Lagrangian points in the Earth–Moon system, where the analogue of the string is the summed (or net) gravitational attraction of the two masses, and the stone is an asteroid or a spacecraft. The Earth–Moon system and the spacecraft all rotate about this combined center of mass, or barycenter. Because the Earth is much heavier than the Moon, the barycenter is located within the Earth (about 1700 km (1,056.3 mi) below the surface). Any object gravitationally held by the rotating Earth–Moon system will be attracted to the barycenter to an equal and opposite degree as its tendency to fly off into space.
Unlike the other Lagrangian points, would exist even in a non-rotating (static or inertial
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
) system. In a rotating system, is a bit farther from the (less massive) Moon and closer to the (more massive) Earth than it would be in a non-rotating system. is slightly unstable (see stability, above) because drifting towards the Moon or Earth increases one gravitational attraction while decreasing the other, causing more drift.
At Lagrangian points , , , and , a spacecraft's inertia to move away from the barycenter is balanced by the attraction of gravity toward the barycenter. and are slightly unstable because small changes in position upset the balance between gravity and inertia, allowing one or the other force to dominate, so that the spacecraft either flies off into space or spirals in toward the barycenter. Stability at and is explained by gravitational equilibrium: if the object were moved into a tighter orbit, it would orbit faster which would counteract the increase in gravity; if the object moves into a wider orbit, the gravity is lower, but it loses speed. The net result is that the object appears constantly to hover or orbit around the or point.
The easiest way to understand the resulting stability is to say , , and positions are as stable as a ball balanced on the tip of a wedge would be stable: any disturbance will toss it out of equilibrium. The , and positions are stable as a ball at the bottom of a bowl would be stable: small perturbations will move it out of place, but it will drift back toward the center of the bowl.
Note that from the perspective of the smaller-mass object — from the moon, in the preceding example — a spacecraft might appear to orbit in an irregular path about the or point, but from the perspective above the orbital plane, it becomes clear that both the smaller mass and the spacecraft are orbiting the larger mass (or more precisely, all of the objects are in orbit around the barycenter of the system); they simply have overlapping orbital paths. This point of view difference is illustrated clearly by animations in the 3753 Cruithne and Coriolis effect
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
articles.
Lagrangian point missions
The Lagrangian point orbits have unique characteristics that have made them a good choice for performing some kinds of missions. These missions generally orbit the points rather than occupy them directly.Past and present missions
| Mission | Lagrangian point | Agency | Status |
|---|---|---|---|
| Advanced Composition Explorer (ACE) Advanced Composition Explorer Advanced Composition Explorer is a NASA space exploration mission being conducted as part of the Explorer program to study matter in situ, comprising energetic particles from the solar wind, the interplanetary medium, and other sources. Real-time data from ACE is used by the Space Weather... |
Sun–Earth | NASA | Operational |
| Solar and Heliospheric Observatory (SOHO) Solar and Heliospheric Observatory The Solar and Heliospheric Observatory is a spacecraft built by a European industrial consortium led by Matra Marconi Space that was launched on a Lockheed Martin Atlas IIAS launch vehicle on December 2, 1995 to study the Sun, and has discovered over 2100 comets. It began normal operations in May... |
Sun–Earth | ESA, NASA | Operational |
| WIND | Sun–Earth | NASA | Operational |
| International Sun/Earth Explorer 3 (ISEE-3) International Cometary Explorer The International Cometary Explorer spacecraft was originally known as International Sun/Earth Explorer 3 satellite, launched August 12, 1978. It was part of the ISEE international cooperative program between NASA and ESRO/ESA to study the interaction between the Earth's magnetic field and the... |
Sun–Earth | NASA | Original mission ended, left point |
| Wilkinson Microwave Anisotropy Probe (WMAP) Wilkinson Microwave Anisotropy Probe The Wilkinson Microwave Anisotropy Probe — also known as the Microwave Anisotropy Probe , and Explorer 80 — is a spacecraft which measures differences in the temperature of the Big Bang's remnant radiant heat — the Cosmic Microwave Background Radiation — across the full sky. Headed by Professor... |
Sun–Earth | NASA | Operational |
| Herschel Herschel Space Observatory The Herschel Space Observatory is a European Space Agency space observatory sensitive to the far infrared and submillimetre wavebands. It is the largest space telescope ever launched, carrying a single mirror of in diameter.... and Planck Space Observatories |
Sun–Earth | ESA | Operational |
| Chang'e 2 Chang'e 2 Chang'e 2 is a Chinese unmanned lunar probe that was launched on 1 October 2010. It was a follow-up to the Chang'e 1 lunar probe, which was launched in 2007. Chang'e 2 was part of the first phase of the Chinese Lunar Exploration Program, and conducted research from a 100-kilometer-high lunar orbit... |
Sun–Earth | CNSA China National Space Administration The China National Space Administration is the national space agency of the People's Republic of China responsible for the national space program. It is responsible for planning and development of space activities... |
Operational |
| ARTEMIS mission extension of THEMIS Themis Themis is an ancient Greek Titaness. She is described as "of good counsel", and is the embodiment of divine order, law, and custom. Themis means "divine law" rather than human ordinance, literally "that which is put in place", from the verb τίθημι, títhēmi, "to put"... |
Earth–Moon and | NASA | Operational |
| GRAIL | Sun–Earth | NASA | Operational |
Future and proposed missions
| Mission | Lagrangian point | Agency | Status |
|---|---|---|---|
| Deep Space Climate Observatory | Sun–Earth | NASA | On hold |
| Solar-C | Sun–Earth | Japan Aerospace Exploration Agency | Possible mission after 2010 |
| Gaia | Sun–Earth | ESA | Planned for Spring 2012 |
| James Webb Space Telescope James Webb Space Telescope The James Webb Space Telescope , previously known as Next Generation Space Telescope , is a planned next-generation space telescope, optimized for observations in the infrared. The main technical features are a large and very cold 6.5 meter diameter mirror, an observing position far from Earth,... |
Sun–Earth | NASA, ESA, Canadian Space Agency | Working on 2018 launch |
| Wide Field Infrared Survey Telescope Wide Field Infrared Survey Telescope The Wide Field Infrared Survey Telescope is a proposed infrared space observatory which was selected by National Research Council committee as the top priority for the next decade of astronomy.... |
Sun–Earth | NASA, U.S. Department of Energy | Proposed for launch in 2020 |
| "Lunar Far-Side Communication Satellites" | Earth–Moon | NASA | Proposed in 1968 |
| Space colonization Lagrange Point Colonization Lagrange point colonization is the colonization of the five equilibrium points in the orbit of a planet or its primary moon, called Lagrange points. The most obvious points for colonization are the points in the Earth-Moon system and the points in the Sun-Earth system... and manufacturing |
Earth–Moon or | L5 Society L5 Society The L5 Society was founded in 1975 by Carolyn and Keith Henson to promote the space colony ideas of Dr Gerard K. O'Neill.The name comes from the and Lagrangian points in the Earth-Moon system proposed as locations for the huge rotating space habitats that Dr O'Neill envisioned... |
Proposed in 1974 |
Natural examples
In the Sun–JupiterJupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
system several thousand asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
s, collectively referred to as Trojan asteroids, are in orbits around the Sun–Jupiter and points. Recent observations suggest that the Sun–Neptune
Neptune
Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times...
and points, known as the Neptune Trojans
Neptune Trojan
Neptune trojans are Kuiper belt object-like bodies in solar orbit that have the same orbital period as Neptune and follow roughly the same orbital path...
, may be very thickly populated, containing large bodies an order of magnitude more numerous than the Jupiter Trojans. Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
has four known co-orbital asteroids (5261 Eureka
5261 Eureka
5261 Eureka is the first asteroid discovered that turned out to be a Mars trojan asteroid. It was discovered by David H. Levy and Henry Holt at Palomar Observatory on June 20, 1990. It trails Mars at a distance varying by only 0.3 AU during each revolution...
, , , and ), all at the Lagrangian points. There is one known Trojan for Earth as of July 2011. Clouds of dust, called Kordylewski cloud
Kordylewski cloud
Kordylewski clouds are large concentrations of dust that may exist at the and Lagrangian points of the Earth–Moon system. They were first reported by Polish astronomer Kazimierz Kordylewski in the 1960s, but there is still controversy as to whether they actually exist, due to their extreme...
s, even fainter than the notoriously weak gegenschein
Gegenschein
The gegenschein is a faint brightening of the night sky in the region of the antisolar point.- Explanation :Like the zodiacal light, the gegenschein is sunlight reflected by interplanetary dust...
, may also be present in the and of the Earth–Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
system.
The Saturnian moon Tethys
Tethys (moon)
Tethys or Saturn III is a mid-sized moon of Saturn about across. It was discovered by G. D. Cassini in 1684 and is named after titan Tethys of Greek mythology. Tethys is pronounced |Odysseus]] is about 400 km in diameter, while the largest graben—Ithaca Chasma is about 100 km wide and...
has two smaller moons in its and points, Telesto
Telesto (moon)
Telesto is a moon of Saturn. It was discovered by Smith, Reitsema, Larson and Fountain in 1980 from ground-based observations, and was provisionally designated '. In the following months, several other apparitions were observed: , , and ....
and Calypso
Calypso (moon)
Calypso is a moon of Saturn. It was discovered in 1980, from ground-based observations, by Dan Pascu, P. Kenneth Seidelmann, William A. Baum, and Douglas G. Currie, and was provisionally designated ' . Several other apparitions of it were recorded in the following months: , , , and...
. The Saturnian moon Dione
Dione (moon)
Dione is a moon of Saturn discovered by Cassini in 1684. It is named after the titan Dione of Greek mythology. It is also designated Saturn IV.- Name :...
also has two Lagrangian co-orbitals, Helene
Helene (moon)
Helene is a moon of Saturn. It was discovered by Pierre Laques and Jean Lecacheux in 1980 from ground-based observations at Pic du Midi Observatory, and was designated . In 1988 it was officially named after Helen of Troy, who was the granddaughter of Cronus in Greek mythology...
at its point and Polydeuces
Polydeuces (moon)
Polydeuces is a very small natural satellite of Saturn that is co-orbital with Dione and librates around the trailing Lagrangian point . Its diameter is estimated to be about 3.5 km....
at . The moons wander azimuthally about the Lagrangian points, with Polydeuces describing the largest deviations, moving up to 32 degrees away from the Saturn–Dione point. Tethys and Dione are hundreds of times more massive than their "escorts" (see the moons' articles for exact diameter figures; masses are not known in several cases), and Saturn is far more massive still, which makes the overall system stable.
Other co-orbitals
2010 TK72010 TK7
2010 TK7 is the first Earth trojan asteroid to be discovered; it precedes Earth in its orbit around the Sun. Trojan objects are most easily conceived as orbiting at a Lagrangian point, a dynamically stable location 60 degrees ahead of or behind a massive orbiting body, in a type of 1:1 orbital...
is the first found Earth Trojan asteroid. It was discovered by the Wide-field Infrared Survey Explorer in October, 2010. After evaluation of the collected data the Trojan character of its motion was published in July 2011. 2010 TK7 has a diameter of 300 meters. Its path is around the Sun–Earth L4 Lagrangian point.
The Earth's companion object 3753 Cruithne
3753 Cruithne
3753 Cruithne is an asteroid in orbit around the Sun in approximate 1:1 orbital resonance with the Earth. It is a periodic inclusion planetoid orbiting the Sun in an apparent horseshoe orbit. It has been incorrectly called "Earth's second moon", but it is only a quasi-satellite. Cruithne never...
is in a relationship with the Earth which is somewhat Trojan-like, but different from a true Trojan. This asteroid occupies one of two regular solar orbits, one of them slightly smaller and faster than the Earth's orbit, and the other slightly larger and slower. The asteroid periodically alternates between these two orbits due to close encounters with Earth. When the asteroid is in the smaller, faster orbit and approaches the Earth, it gains orbital energy from the Earth and moves up into the larger, slower orbit. It then falls farther and farther behind the Earth, and eventually Earth approaches it from the other direction. Then the asteroid gives up orbital energy to the Earth, and drops back into the smaller orbit, thus beginning the cycle anew. The cycle has no noticeable impact on the length of the year, because Earth's mass is over 20 billion
1000000000 (number)
1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109....
times more than 3753 Cruithne.
Epimetheus
Epimetheus (moon)
Epimetheus is an inner satellite of Saturn. It is also known as Saturn XI. It is named after the mythological Epimetheus, brother of Prometheus.-Discovery:Epimetheus occupies essentially the same orbit as the moon Janus...
and Janus
Janus (moon)
Janus is an inner satellite of Saturn. It is also known as Saturn X . It is named after the mythological Janus.-Discovery and orbit:Janus occupies practically the same orbit as the moon Epimetheus...
, satellites of Saturn, have a similar relationship, though they are of similar masses and so actually exchange orbits with each other periodically. (Janus is roughly 4 times more massive but still light enough for its orbit to be altered.) Another similar configuration is known as orbital resonance
Orbital resonance
In celestial mechanics, an orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. Orbital resonances greatly enhance the mutual gravitational influence of...
, in which orbiting bodies tend to have periods of a simple integer ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
, due to their interaction.
See also
- Euler's three-body problemEuler's three-body problemIn physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
- List of objects at Lagrangian points
- Lunar space elevatorLunar space elevatorA lunar space elevator is a proposed cable running from the surface of the Moon into space.It is similar in concept to the better known Earth space elevator idea...
- Home on Lagrange (The L5 Song)Home on Lagrange (The L5 Song)Home on Lagrange is a filk song, written in 1977 by William S. Higgins and Barry D. Gehm, intended to be sung to the tune of Home on the Range...
- L5 SocietyL5 SocietyThe L5 Society was founded in 1975 by Carolyn and Keith Henson to promote the space colony ideas of Dr Gerard K. O'Neill.The name comes from the and Lagrangian points in the Earth-Moon system proposed as locations for the huge rotating space habitats that Dr O'Neill envisioned...
- Horseshoe orbitHorseshoe orbitA horseshoe orbit is a type of co-orbital motion of a small orbiting body relative to a larger orbiting body . The orbital period of the smaller body is very nearly the same as for the larger body, and its path appears to have a horseshoe shape in a rotating reference frame as viewed from the...
- Hill sphereHill sphereAn astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own...
- Lagrange point colonizationLagrange Point ColonizationLagrange point colonization is the colonization of the five equilibrium points in the orbit of a planet or its primary moon, called Lagrange points. The most obvious points for colonization are the points in the Earth-Moon system and the points in the Sun-Earth system...
- Lissajous orbitLissajous orbitIn orbital mechanics, a Lissajous orbit, , named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbits around a libration point are curved paths that lie...
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- GegenscheinGegenscheinThe gegenschein is a faint brightening of the night sky in the region of the antisolar point.- Explanation :Like the zodiacal light, the gegenschein is sunlight reflected by interplanetary dust...
- Co-orbital configurationCo-orbital configurationIn astronomy, a co-orbital configuration refers to two or more celestial objects that orbit at the same, or very similar, distance from their parent object as each other, i.e. they are in a 1:1 mean motion resonance....
- Trojan planet
External links
- Joseph-Louis, Comte Lagrange, from Oeuvres Tome 6, "Essai sur le Problème des Trois Corps" - Essai (PDF); source Tome 6 (Viewer)
- "Essay on the Three-Body Problem" by J-L Lagrange, translated from the above, in http://www.merlyn.demon.co.uk/essai-3c.htm.
- De motu rectilineo trium corporum se mutuo attrahentium - Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
- PDF 227kB - very rough translation at http://www.merlyn.demon.co.uk/essai-3c.htm. - What are Lagrange points? — European Space AgencyEuropean Space AgencyThe European Space Agency , established in 1975, is an intergovernmental organisation dedicated to the exploration of space, currently with 18 member states...
page, with good animations - Explanation of Lagrange points – Prof. Neil J. Cornish
- A NASA explanation – also attributed to Neil J. Cornish
- Explanation of Lagrange points – Prof. John Baez
- Geometry and calculations of Lagrange points – Dr J R Stockton
- Locations of Lagrange points, with approximations – Dr. David Peter Stern
- An online calculator to compute the precise positions of the 5 Lagrange points for any 2-body system – Tony Dunn
- Astronomy cast — Ep. 76: Lagrange Points Fraser Cain and Dr. Pamela Gay
- The Five Points of Lagrange by Neil deGrasse TysonNeil deGrasse TysonNeil deGrasse Tyson is an American astrophysicist, a science communicator, the Frederick P. Rose Director of the Hayden Planetarium at the Rose Center for Earth and Space, and a Research Associate in the Department of Astrophysics at the American Museum of Natural History...
- Earth, a lone Trojan discovered