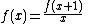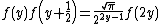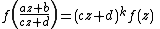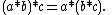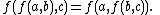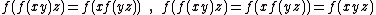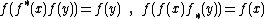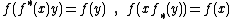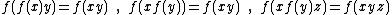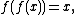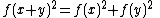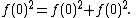Functional equation
Encyclopedia
In mathematics
, a functional equation is any equation that specifies a function in implicit form
.
Often, the equation
relates the value of a function (or functions) at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional equations they satisfy. The term functional equation usually refers to equations that cannot be simply reduced to algebraic equations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a functional equation is any equation that specifies a function in implicit form
Implicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
.
Often, the equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
relates the value of a function (or functions) at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional equations they satisfy. The term functional equation usually refers to equations that cannot be simply reduced to algebraic equations.
Examples
- The functional equation
-
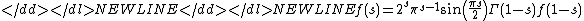
- is satisfied by the Riemann zeta function ζ. The capital Γ denotes the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
- These functional equations are satisfied by the gamma function. The gamma function is the unique solution of the system of all three equations:
-
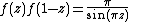 (Euler'sLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(Euler'sLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
reflection formulaReflection formulaIn mathematics, a reflection formula or reflection relation for a function f is a relationship between f and f...
)
- The functional equation
- where a, b, c, d are integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s satisfying ad − bc = 1, i.e.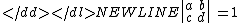 , defines f to be a modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
, defines f to be a modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of order k.
- Miscellaneous examples not necessarily involving "famous" functions:
-
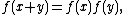 satisfied by all exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
satisfied by all exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s
-
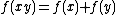 , satisfied by all logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, satisfied by all logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic functions
-
 (Cauchy functional equation)
(Cauchy functional equation)
-
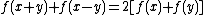 (quadratic equation or parallelogram lawParallelogram lawIn mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...
(quadratic equation or parallelogram lawParallelogram lawIn mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...
)
-
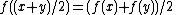 (Jensen)
(Jensen)
-
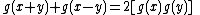 (d'Alembert)
(d'Alembert)
-
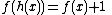 (Abel equationAbel equationThe Abel equation, named after Niels Henrik Abel, is special case of functional equations which can be written in the formf = h\,\!or\alpha=\alpha+1\!and shows non-trivial properties at the iteration.-Equivalence:...
(Abel equationAbel equationThe Abel equation, named after Niels Henrik Abel, is special case of functional equations which can be written in the formf = h\,\!or\alpha=\alpha+1\!and shows non-trivial properties at the iteration.-Equivalence:...
)
-
 (Schröder's equation).
(Schröder's equation).
- A simple form of functional equation is a recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
. This, formally speaking, involves an unknown function on integers, and also translation operators.
- One such example of a recurrence relation is
-
-

- The commutative and associative laws are functional equations. When the associative law is expressed in its familiar form, one lets some symbol between two variables represent a binary operation, thus:
-
But if we write ƒ(a, b) instead of a * b then the associative law looks more like what one conventionally thinks of as a functional equation:
One thing that all of the examples listed above share in common is that in each case two or more known functions (sometimes multiplication by a constant, sometimes addition of two variables, sometimes the identity function) are substituted into the unknown function to be solved for.
- The b-integer and b-decimal parts of real numbers were introduced and studied by M.H.Hooshmand. The b-parts real functions have many interesting number theoretic explanations, analytic and algebraic properties, and satisfy the functional equation:
The following functional equations are as a generalization of the b-parts functional equation for semigroups and groups, even in a binary system (magma), that are introduced by him:
Associative equations ;
Decomposer equations ;
Strong decomposer equations ;
Canceler equations ;
where ƒ*(x)ƒ(x) = ƒ(x)ƒ*(x) = x.
In
,
the general solution of the decomposer and strong decomposer equations are introduced in the sets with a binary operation and semigroups respectively and also associative equations in arbitrary groups. In that paper it is proven that the associative equations and the system of strong decomposer and canceler equations do not have any nontrivial solutions in the simple groups.
When it comes to asking for all solutions, it may be the case that conditions from mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
should be applied; for example, in the case of the Cauchy equation mentioned above, the solutions that are continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s are the 'reasonable' ones, while other solutions that are not likely to have practical application can be constructed (by using a Hamel basis for the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s). The Bohr–Mollerup theorem is another well-known example.
Solving functional equations
Solving functional equations can be very difficult but there are some common methods of solving them. For example, in dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
a variety of successive approximation methods are used to solve Bellman's functional equationBellman equationA Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
, including methods based on fixed point iterations. The main method of solving elementary functional equations is substitution. It is often useful to prove surjectivity or injectivity and prove oddness or evenness, if possible. It is also useful to guess possible solutions. Induction is a useful technique to use when the function is only defined for rational values.
A discussion of involutary functions is useful. For example, consider the function
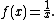
Then consider
if we continue the pattern we end up with x for an even number of compositions and ƒ(x) for an odd number. This same idea applies to many other functions, e.g.
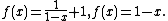
Example 1: Solve
for all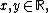 assuming ƒ is a real-valued functionReal-valued functionIn mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
assuming ƒ is a real-valued functionReal-valued functionIn mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
.
Let x = y = 0
So ƒ(0)2 = 0 and ƒ(0) = 0.
Now, let y = −x:
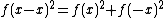
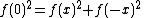
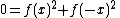
A square of a real number is nonnegative, and a sum of nonnegative numbers is zero iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
both numbers are 0. So ƒ(x)2 = 0 for all x and ƒ(x) = 0 is the only solution.
External links
- Functional Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
- Functional Equations: Index at EqWorld: The World of Mathematical Equations.
- IMO Compendium text on functional equations in problem solving.
- is satisfied by the Riemann zeta function ζ. The capital Γ denotes the gamma function