
Absolute convergence
Encyclopedia
In mathematics
, a series
(or sometimes also an integral
) of numbers is said to converge absolutely if the sum (or integral) of the absolute value
of the summand or integrand is finite. More precisely, a real or complex series is said to converge absolutely if
is said to converge absolutely if 
Absolute convergence is important to the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess, yet is broad enough to occur commonly.
 whose terms
whose terms 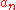 are elements of an arbitrary abelian topological group
are elements of an arbitrary abelian topological group
. The notion of absolute convergence requires more structure, namely a norm
:
A norm on an abelian group G (written additively, with identity element 0) is a real-valued function
on G such that:
Then the function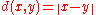 induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if
induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if 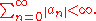
In particular, for series with values in any Banach space
, absolute convergence implies convergence. The converse is also true: if absolute convergence implies convergence in a normed space, then the space is a Banach space.
If a series is convergent but not absolutely convergent, it is called conditionally convergent. An example of a conditionally convergent series is the alternating harmonic series. Many standard tests for divergence and convergence, most notably including the ratio test and the root test, demonstrate absolute convergence. This is because a power series is absolutely convergent on the interior of its disk of convergence.
 is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that
is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that 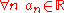 .
.
Then, is convergent.
is convergent.
Since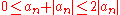 , we have:
, we have: .
.
Thus,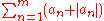 is a bounded monotonic sequence (in m), which must converge.
is a bounded monotonic sequence (in m), which must converge.
 is a difference of convergent series; therefore, it is also convergent.
is a difference of convergent series; therefore, it is also convergent.
 is convergent
is convergent  is convergent.
is convergent.
Given a series with values in a normed abelian group G and
with values in a normed abelian group G and
a permutation
 of the natural numbers, one builds a new series
of the natural numbers, one builds a new series
 , said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.
, said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.
When G is complete, absolute convergence implies unconditional convergence.
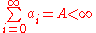 ,
,  and let
and let  be a permutation of
be a permutation of  , then
, then 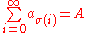
 , we can choose some
, we can choose some 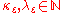 , such that
, such that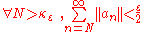
and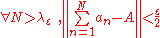 .
.
let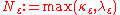 ,
,
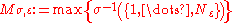 .
.
For any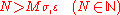 , let
, let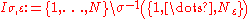 ,
,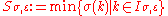 (note.
(note. ), and
), and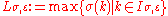
then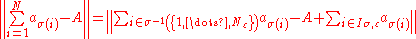
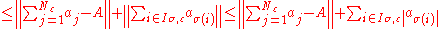
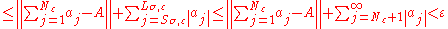
therefore
then
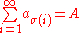
Q.E.D.
The issue of the converse is much more interesting. For real series it follows from the Riemann rearrangement theorem that unconditional convergence implies absolute convergence. Since a series with values in a finite-dimensional normed space is absolutely convergent if each of its one-dimensional projections is absolutely convergent, it follows easily that absolute and unconditional convergence coincide for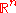 -valued series.
-valued series.
But there is an unconditionally and nonabsolutely convergent series with values in Hilbert space
 : if
: if 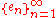 is an orthonormal basis, take
is an orthonormal basis, take  .
.
A theorem of Dvoretzky-Rogers asserts that every infinite-dimensional Banach space admits an unconditionally but non-absolutely convergent series.
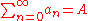
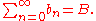
The Cauchy product is defined as the sum of terms where:
where:

Then, if either the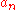 or
or 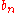 sum converges absolutely, then
sum converges absolutely, then

 of a real or complex-valued function is said to converge absolutely if
of a real or complex-valued function is said to converge absolutely if 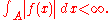 One also says that
One also says that  is absolutely integrable.
is absolutely integrable.
When is a closed bounded interval, every continuous function is integrable, and since
is a closed bounded interval, every continuous function is integrable, and since  continuous implies
continuous implies 
continuous, similarly every continuous function is absolutely integrable. It is not generally true that absolutely integrable functions on
are integrable: let be a nonmeasurable subset and take
be a nonmeasurable subset and take 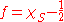 , where
, where  is the
is the
characteristic function of S. Then is not Lebesgue measurable but
is not Lebesgue measurable but  is constant.
is constant.
However, it is a standard result that if is Riemann integrable, so is
is Riemann integrable, so is  . This holds also for the Lebesgue integral; see below. On the other hand a function
. This holds also for the Lebesgue integral; see below. On the other hand a function  may be Kurzweil-Henstock integrable (or "gauge integrable") while
may be Kurzweil-Henstock integrable (or "gauge integrable") while  is not. This includes the case of improperly Riemann integrable functions.
is not. This includes the case of improperly Riemann integrable functions.
Similarly, when is an interval of infinite length it is well-known that there are improperly Riemann integrable functions
is an interval of infinite length it is well-known that there are improperly Riemann integrable functions  which are not absolutely integrable. Indeed, given any series
which are not absolutely integrable. Indeed, given any series  one can consider the associated step function
one can consider the associated step function 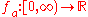 defined
defined
by . Then
. Then  converges absolutely,
converges absolutely,
converges conditionally or diverges according to the corresponding behavior of

Another example of a convergent but not
absolutely convergent improper Riemann integral is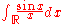 .
.
On any measure space A the Lebesgue integral of a real-valued function is defined in
terms of its positive and negative parts, so the facts:
are essentially built into the definition of the Lebesgue integral. In particular, applying the theory to the counting measure on a set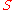 , one recovers the notion of unordered summation of series developed by Moore-Smith using (what are
, one recovers the notion of unordered summation of series developed by Moore-Smith using (what are
now called) nets. When is the set of natural numbers,
is the set of natural numbers,
Lebesgue integrability, unordered summability and absolute convergence all coincide.
Finally, all of the above holds for integrals with values in a Banach space. The definition
of a Banach-valued Riemann integral is an evident modification of the usual one. For the
Lebesgue integral one needs to circumvent the decomposition into positive and negative parts
with Daniell's more functional analytic approach, obtaining the Bochner integral
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
(or sometimes also an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
) of numbers is said to converge absolutely if the sum (or integral) of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the summand or integrand is finite. More precisely, a real or complex series
 is said to converge absolutely if
is said to converge absolutely if 
Absolute convergence is important to the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess, yet is broad enough to occur commonly.
Background
One may study the convergence of series whose terms
whose terms 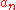 are elements of an arbitrary abelian topological group
are elements of an arbitrary abelian topological groupTopological abelian group
In mathematics, a topological abelian group, or TAG, is a topological group that is also an abelian group.That is, a TAG is both a group and a topological space, the group operations are continuous, and the group's binary operation is commutative....
. The notion of absolute convergence requires more structure, namely a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
:
A norm on an abelian group G (written additively, with identity element 0) is a real-valued function

on G such that:
- The norm of the identity element of G is zero:
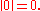
- For every x in G,
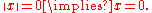
- For every x in G,
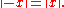
- For every x, y in G,

Then the function
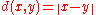 induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if
induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if 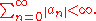
Relation to convergence
If the metric d on G is complete, then every absolutely convergent series is convergent. The proof is the same as for complex-valued series: use the completeness to derive the Cauchy criterion for convergence—a series is convergent if and only if its tails can be made arbitrarily small in norm—and apply the triangle inequality.In particular, for series with values in any Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, absolute convergence implies convergence. The converse is also true: if absolute convergence implies convergence in a normed space, then the space is a Banach space.
If a series is convergent but not absolutely convergent, it is called conditionally convergent. An example of a conditionally convergent series is the alternating harmonic series. Many standard tests for divergence and convergence, most notably including the ratio test and the root test, demonstrate absolute convergence. This is because a power series is absolutely convergent on the interior of its disk of convergence.
Proof that any absolutely convergent series is convergent
Assume is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that
is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that 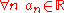 .
.Then,
 is convergent.
is convergent.Since
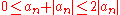 , we have:
, we have: .
.Thus,
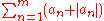 is a bounded monotonic sequence (in m), which must converge.
is a bounded monotonic sequence (in m), which must converge. is a difference of convergent series; therefore, it is also convergent.
is a difference of convergent series; therefore, it is also convergent. is convergent
is convergent  is convergent.
is convergent.Rearrangements and unconditional convergence
In the general context of a G-valued series, a distinction is made between absolute and unconditional convergence, and the assertion that a real or complex series which is not absolutely convergent is necessarily conditionally convergent (meaning not unconditionally convergent) is then a theorem, not a definition. This is discussed in more detail below.Given a series
 with values in a normed abelian group G and
with values in a normed abelian group G anda permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
 of the natural numbers, one builds a new series
of the natural numbers, one builds a new series , said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.
, said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.When G is complete, absolute convergence implies unconditional convergence.
Theorem
Let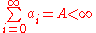 ,
,  and let
and let  be a permutation of
be a permutation of  , then
, then 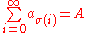
Proof
For any , we can choose some
, we can choose some 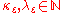 , such that
, such that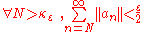
and
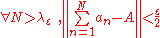 .
.let
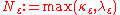 ,
,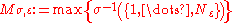 .
.For any
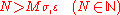 , let
, let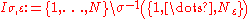 ,
,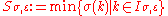 (note.
(note. ), and
), and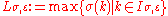
then
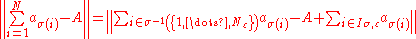
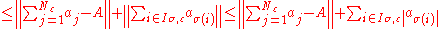
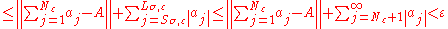
therefore

then
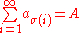
Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
The issue of the converse is much more interesting. For real series it follows from the Riemann rearrangement theorem that unconditional convergence implies absolute convergence. Since a series with values in a finite-dimensional normed space is absolutely convergent if each of its one-dimensional projections is absolutely convergent, it follows easily that absolute and unconditional convergence coincide for
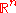 -valued series.
-valued series.But there is an unconditionally and nonabsolutely convergent series with values in Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
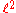 : if
: if 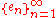 is an orthonormal basis, take
is an orthonormal basis, take  .
.A theorem of Dvoretzky-Rogers asserts that every infinite-dimensional Banach space admits an unconditionally but non-absolutely convergent series.
Products of series
The Cauchy product of two series converges to the product of the sums if at least one of the series converges absolutely. That is, suppose: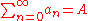
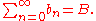
The Cauchy product is defined as the sum of terms
 where:
where:
Then, if either the
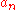 or
or 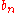 sum converges absolutely, then
sum converges absolutely, then
Absolute convergence of integrals
The integral of a real or complex-valued function is said to converge absolutely if
of a real or complex-valued function is said to converge absolutely if 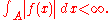 One also says that
One also says that  is absolutely integrable.
is absolutely integrable.When
 is a closed bounded interval, every continuous function is integrable, and since
is a closed bounded interval, every continuous function is integrable, and since  continuous implies
continuous implies 
continuous, similarly every continuous function is absolutely integrable. It is not generally true that absolutely integrable functions on

are integrable: let
 be a nonmeasurable subset and take
be a nonmeasurable subset and take 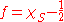 , where
, where  is the
is thecharacteristic function of S. Then
 is not Lebesgue measurable but
is not Lebesgue measurable but  is constant.
is constant.However, it is a standard result that if
 is Riemann integrable, so is
is Riemann integrable, so is  . This holds also for the Lebesgue integral; see below. On the other hand a function
. This holds also for the Lebesgue integral; see below. On the other hand a function  may be Kurzweil-Henstock integrable (or "gauge integrable") while
may be Kurzweil-Henstock integrable (or "gauge integrable") while  is not. This includes the case of improperly Riemann integrable functions.
is not. This includes the case of improperly Riemann integrable functions.Similarly, when
 is an interval of infinite length it is well-known that there are improperly Riemann integrable functions
is an interval of infinite length it is well-known that there are improperly Riemann integrable functions  which are not absolutely integrable. Indeed, given any series
which are not absolutely integrable. Indeed, given any series  one can consider the associated step function
one can consider the associated step function 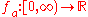 defined
definedby
 . Then
. Then  converges absolutely,
converges absolutely,converges conditionally or diverges according to the corresponding behavior of

Another example of a convergent but not
absolutely convergent improper Riemann integral is
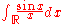 .
.On any measure space A the Lebesgue integral of a real-valued function is defined in
terms of its positive and negative parts, so the facts:
-
 integrable implies
integrable implies  integrable
integrable -
 measurable,
measurable,  integrable implies
integrable implies  integrable
integrable
are essentially built into the definition of the Lebesgue integral. In particular, applying the theory to the counting measure on a set
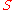 , one recovers the notion of unordered summation of series developed by Moore-Smith using (what are
, one recovers the notion of unordered summation of series developed by Moore-Smith using (what arenow called) nets. When
 is the set of natural numbers,
is the set of natural numbers,Lebesgue integrability, unordered summability and absolute convergence all coincide.
Finally, all of the above holds for integrals with values in a Banach space. The definition
of a Banach-valued Riemann integral is an evident modification of the usual one. For the
Lebesgue integral one needs to circumvent the decomposition into positive and negative parts
with Daniell's more functional analytic approach, obtaining the Bochner integral
Bochner integral
In mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.-Definition:...
.
See also
- Convergence of Fourier seriesConvergence of Fourier seriesIn mathematics, the question of whether the Fourier series of a periodic function converges to the given function is researched by a field known as classical harmonic analysis, a branch of pure mathematics...
- Conditional convergence
- Modes of convergence (annotated index)Modes of convergence (annotated index)The purpose of this article is to serve as an annotated index of various modes of convergence and their logical relationships. For an expository article, see Modes of convergence...
- Cauchy principal valueCauchy principal valueIn mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
- A counterexample related to Fubini's theorem
- 1/2 − 1/4 + 1/8 − 1/16 + · · ·
- 1/2 + 1/4 + 1/8 + 1/16 + · · ·

