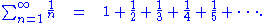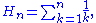.gif)
Harmonic series (mathematics)
Encyclopedia
In mathematics
, the harmonic series is the divergent
infinite series:
Its name derives from the concept of overtone
s, or harmonics in music
: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength
. Every term of the series after the first is the harmonic mean
of the neighboring terms; the term harmonic mean likewise derives from music.
, Johann Bernoulli
, and Jakob Bernoulli.
Historically, harmonic sequences have had a certain popularity with architects. This was so particularly in the Baroque
period, when architects used them to establish the proportions
of floor plans, of elevations, and to establish harmonic relationships between both interior and exterior architectural details of churches and palaces.
though the limit of the nth term as n goes to infinity is zero. The divergence of the harmonic series is also the source of some apparent paradox
es. One example of these is the "worm on the rubber band
". Suppose that a worm crawls along a 1 metre rubber band and, after each minute, the rubber band is uniformly stretched by an additional 1 metre. If the worm travels 1 centimetre per minute, will the worm ever reach the end of the rubber band? The answer, counterintuitively, is "yes", for after n minutes, the ratio of the distance travelled by the worm to the total length of the rubber band is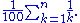
Because the series gets arbitrarily large as n becomes larger, eventually this ratio must exceed 1, which implies that the worm reaches the end of the rubber band. The value of n at which this occurs must be extremely large, however, approximately e100, a number exceeding 1040. Although the harmonic series does diverge, it does so very slowly.
Another example is: given a collection of identical dominoes, it is clearly possible to stack them at the edge of a table so that they hang over the edge of the table. The counterintuitive result is that one can stack them in such a way as to make the overhang arbitrarily large, provided there are enough dominoes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the harmonic series is the divergent
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
infinite series:
Its name derives from the concept of overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
s, or harmonics in music
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
. Every term of the series after the first is the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the neighboring terms; the term harmonic mean likewise derives from music.
History
The fact that the harmonic series diverges was first proven in the 14th century by Nicole Oresme, but this achievement fell into obscurity. Proofs were given in the 17th century by Pietro MengoliPietro Mengoli
Pietro Mengoli was an Italian mathematician and clergyman from Bologna, where he studied with Bonaventura Cavalieri at the University of Bologna, and succeeded him in 1647...
, Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
, and Jakob Bernoulli.
Historically, harmonic sequences have had a certain popularity with architects. This was so particularly in the Baroque
Baroque
The Baroque is a period and the style that used exaggerated motion and clear, easily interpreted detail to produce drama, tension, exuberance, and grandeur in sculpture, painting, literature, dance, and music...
period, when architects used them to establish the proportions
Proportion (architecture)
Proportion is the relation between elements and a whole.-Architectural proportions:In architecture the whole is not just a building but the set and setting of the site. The things that make a building and its site "well shaped" include the orientation of the site and the buildings on it to the...
of floor plans, of elevations, and to establish harmonic relationships between both interior and exterior architectural details of churches and palaces.
Paradoxes
The harmonic series is counterintuitive to students first encountering it, because it is a divergent seriesDivergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
though the limit of the nth term as n goes to infinity is zero. The divergence of the harmonic series is also the source of some apparent paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es. One example of these is the "worm on the rubber band
Ant on a rubber rope
Ant on a rubber rope is a mathematical puzzle with a solution that appears counter-intuitive or paradoxical. It is sometimes given as a worm, or inchworm, on a rubber or elastic band, but the principles of the puzzle remain the same....
". Suppose that a worm crawls along a 1 metre rubber band and, after each minute, the rubber band is uniformly stretched by an additional 1 metre. If the worm travels 1 centimetre per minute, will the worm ever reach the end of the rubber band? The answer, counterintuitively, is "yes", for after n minutes, the ratio of the distance travelled by the worm to the total length of the rubber band is
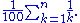
Because the series gets arbitrarily large as n becomes larger, eventually this ratio must exceed 1, which implies that the worm reaches the end of the rubber band. The value of n at which this occurs must be extremely large, however, approximately e100, a number exceeding 1040. Although the harmonic series does diverge, it does so very slowly.
Another example is: given a collection of identical dominoes, it is clearly possible to stack them at the edge of a table so that they hang over the edge of the table. The counterintuitive result is that one can stack them in such a way as to make the overhang arbitrarily large, provided there are enough dominoes.
Divergence
There are several well-known proofs of the divergence of the harmonic series. Two of them are given below.Comparison test
One way to prove divergence is to compare the harmonic series with another divergent series:-
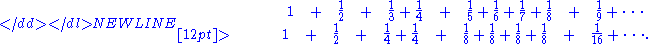
Each term of the harmonic series is greater than or equal to the corresponding term of the second series, and therefore the sum of the harmonic series must be greater than the sum of the second series. However, the sum of the second series is infinite: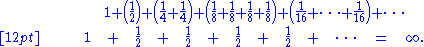
It follows (by the comparison testComparison testIn mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
) that the sum of the harmonic series must be infinite as well. More precisely, the comparison above proves that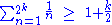
for every positive integer k.
This proof, due to Nicole Oresme, is considered by some a high point of medieval mathematics. It is still a standard proof taught in mathematics classes today. Cauchy's condensation test is a generalization of this argument.
Integral test
It is possible to prove that the harmonic series diverges by comparing its sum with an improper integralImproper integralIn calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
. Specifically, consider the arrangement of rectangles shown in the figure to the right. Each rectangle is 1 unit wide and 1 / n units high, so the total area of the rectangles is the sum of the harmonic series:
However, the total area under the curve y = 1 / x from 1 to infinity is given by an improper integralImproper integralIn calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
: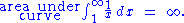
Since this area is entirely contained within the rectangles, the total area of the rectangles must be infinite as well. More precisely, this proves that
The generalization of this argument is known as the integral test.
Rate of divergence
The harmonic series diverges very slowly. For example, the sum of the first 1043 terms is less than 100. This is because the partial sums of the series have logarithmic growthLogarithmic growthIn mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. y = C log . Note that any logarithm base can be used, since one can be converted to another by a fixed constant...
. In particular,
where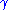 is the Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
is the Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
and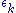 ~
~ 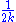 which approaches 0 as
which approaches 0 as  goes to infinity. This result is due to Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
goes to infinity. This result is due to Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. He proved also the more striking fact that the sum which includes only the reciprocals of primes already diverges, i.e.
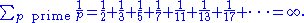
Partial sums
The nth partial sum of the diverging harmonic series,
is called the nth harmonic number.
The difference between the nth harmonic number and the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of n converges to the Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
The difference between distinct harmonic numbers is never an integer.
No harmonic numbers are integers, except for n = 1.
Alternating harmonic series
The series
-
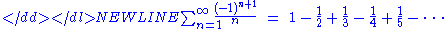
is known as the alternating harmonic series. This series converges by the alternating series testAlternating series testThe alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.A series of the form...
. In particular, the sum is equal to the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of 2: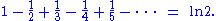
This formula is a special case of the Mercator series, the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the natural logarithm.
A related series can be derived from the Taylor series for the arctangent:-
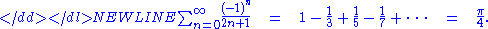
This is known as the Leibniz formula for pi.
General harmonic series
The general harmonic series is of the form

where and
and  are real numbers.
are real numbers.
By the comparison testComparison testIn mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
, all general harmonic series diverge.
P-series
A generalization of the harmonic series is the p-series, defined as:
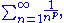
for any positive real number p. When p = 1, the p-series is the harmonic series, which diverges. Either the integral test or the Cauchy condensation test shows that the p-series converges for all p > 1 (in which case it is called the over-harmonic series) and diverges for all p ≤ 1. If p > 1 then the sum of the p-series is ζ(p), i.e., the Riemann zeta function evaluated at p.
φ-series
For any convex, real-valued function φ such that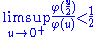
the series is convergent.
Random harmonic series
The random harmonic series
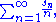
where the sn are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, identically distributed random variables taking the values +1 and −1 with equal probability 1/2, is a well-known example in probability theory for a series of random variables that converges with probability 1Almost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
. The fact of this convergence is an easy consequence of either the Kolmogorov three-series theoremKolmogorov's three-series theoremIn probability theory, Kolmogorov's three-series theorem, named after Andrey Kolmogorov, gives a criterion for the almost sure convergence of an infinite series of random variables in terms of the convergence of three different series involving properties of their probability distributions.-...
or of the closely related Kolmogorov maximal inequalityKolmogorov's inequalityIn probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound...
. Byron Schmuland of the University of Alberta further examined the properties of the random harmonic series, and showed that the convergent is a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with some interesting properties. In particular, the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of this random variable evaluated at +2 or at −2 takes on the value , differing from 1/8 by less than 10−42. Schmuland's paper explains why this probability is so close to, but not exactly, 1/8. The exact value of this probability is given by the infinite cosine product integral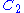 divided by π.
divided by π.
Depleted harmonic series
The depleted harmonic series where all of the terms in which the digit 9 appears anywhere in the denominator are removed can be shown to converge and its value is less than 80. In fact when terms containing any particular string of digits are removed the series converges.
See also
- Complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
- Lagarias's theorem
- Harmonic progression
External links
- "The Harmonic Series Diverges Again and Again", The AMATYC Review, 27 (2006), pp. 31–43. Many proofs of divergence of harmonic series.
- Complex logarithm
-
-