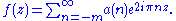Modular form
Encyclopedia
In mathematics
, a modular form is a (complex) analytic function
on the upper half-plane satisfying a certain kind of functional equation
and growth condition. The theory of modular forms therefore belongs to complex analysis
but the main importance of the theory has traditionally been in its connections with number theory
. Modular forms appear in other areas, such as algebraic topology
and string theory
.
A modular function is a modular form, without the condition that f(z) be holomorphic at infinity. Instead, modular functions are meromorphic at infinity.
Modular form theory is a special case of the more general theory of automorphic form
s, and therefore can now be seen as just the most concrete part of a rich theory of discrete group
s.
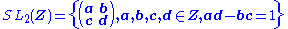
is a complex-valued function f on satisfying the following three conditions: firstly, f is a holomorphic function
on H. Secondly, for any z in H and any matrix in SL2(Z) as above, the equation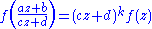
is required to hold. Thirdly, f is required to be holomorphic as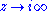
. The latter condition is also phrased by saying that f is "holomorphic at the cusp", a terminology that is explained below. The weight k is typically a positive integer.
The second condition, with the matrices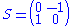
and 
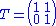reads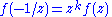
and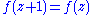
respectively. Since S and T generate the modular group
SL2(Z), the second condition above is equivalent to these two equations.
s which satisfies certain conditions:
If we consider the lattice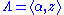
generated by a constant α and a variable z, then F(Λ) is an analytic function
of z.
If α is a non-zero complex number and αΛ is the lattice obtained by multiplying each element of Λ by α, then F(αΛ) = α−kF(Λ) where k is a constant (typically a positive integer) called the weight of the form.
The absolute value
of F(Λ) remains bounded above as long as the absolute value of the smallest non-zero element in Λ is bounded away from 0.
The key idea in proving the equivalence of the two definitions is that such a function F is determined, because of the first property, by its values on lattices of the form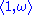
, where ω ∈ H.
it satisfies the following properties:
It is often written in terms of as
(the square of the nome),
This is also referred to as the q-expansion of f (see also q-analog
). The coefficients a(n) are known as the Fourier coefficients of f, the number m is called the order of the pole of f at
.
Another way to phrase the definition of modular functions is to use elliptic curve
s: every lattice Λ determines an elliptic curve
C/Λ over C; two lattices determine isomorphic elliptic curves if and only if one is obtained from the other by multiplying by some non-zero complex number α. Thus, a modular function can also be regarded as a meromorphic function on the set of isomorphism classes of elliptic curves. For example, the j-invariant
j(z) of an elliptic curve, regarded as a function on the set of all elliptic curves, is a modular function. More conceptually, modular functions can be thought of as functions on the moduli space of isomorphism classes of complex elliptic curves.
A modular form f that vanishes at
(equivalently, a(0) = 0, also paraphrased as z = i∞) is called a cusp form
(Spitzenform in German
). The smallest n such that a(n) ≠ 0 is the order of the zero of f at i∞.
. Such a group G acts
on H in the same way as SL(2, Z). The quotient topological space G\H can be shown to be a Hausdorff space
. Typically it is not compact, but can be compactified by adding a finite number of points called cusps. These are points at the boundary of H, i.e., either in Q, the rationals, or ∞, such that there is a parabolic element of G (a matrix with trace ±2) fixing the point. Here, a matrix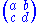
sends ∞ to a/c. This yields a compact topological space G\H∗. What is more, it can be endowed with the structure of a Riemann surface
, which allows to speak of holo- and meromorphic functions.
Important examples are, for any positive integer N, either one of the congruence subgroup
s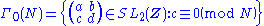
and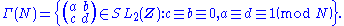
For G = Γ0(N) or Γ(N), the spaces G\H and G\H∗ are denoted Y0(N) and X0(N) and Y(N), X(N), respectively.
The geometry of G\H∗ can be understood by studying fundamental domain
s for G, i.e. subsets D ⊂ H such that D intersects each orbit of the G-action on H exactly once and such that the closure of D meets all orbits. For example, the genus
of G\H∗ can be computed.
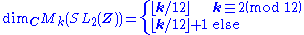
where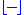
denotes the floor function
.
The modular functions constitute the field of functions
of the Riemann surface, and hence form a field of transcendence degree
one (over C). If a modular function f is not identically 0, then it can be shown that the number of zeroes of f is equal to the number of poles of f in the closure
of the fundamental region RΓ.It can be shown that the field of modular function of level N (N ≥ 1) is generated by the functions j(z) and j(Nz).
P(V): in that setting, one would ideally like functions F on the vector space V which are polynomial in the coordinates of v≠ 0 in V and satisfy the equation F(cv) = F(v) for all non-zero c. Unfortunately, the only such functions are constants. If we allow denominators (rational functions instead of polynomials), we can let F be the ratio of two homogeneous
polynomials of the same degree. Alternatively, we can stick with polynomials and loosen the dependence on c, letting F(cv) = ckF(v). The solutions are then the homogeneous polynomials of degree k. On the one hand, these form a finite dimensional vector space for each k, and on the other, if we let k vary, we can find the numerators and denominators for constructing all the rational functions which are really functions on the underlying projective space P(V).
One might ask, since the homogeneous polynomials are not really functions on P(V), what are they, geometrically speaking? The algebro-geometric
answer is that they are sections of a sheaf
(one could also say a line bundle
in this case). The situation with modular forms is precisely analogous.
Modular forms can also be profitably approached from this geometric direction, as sections of line bundles on the moduli space of elliptic curves.
), it is called an entire modular form.
If f is meromorphic but not holomorphic at the cusp, it is called a non-entire modular form. For example, the j-invariant
is a non-entire modular form of weight 0, and has a simple pole at
.
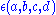with 
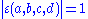to appear in the transformation, so that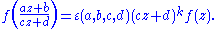
Functions of the form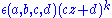
are known as automorphic factor
s.
By allowing automorphic factors, functions such as the Dedekind eta function
may be encompassed by the theory, being a modular form of weight 1/2. Thus, for example, let
be a Dirichlet character
mod N. A modular form of weight k, level N (or level group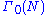
) with nebentypus the Dirichlet character 
is a holomorphic function
f on the upper half-plane such that for any
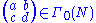
and any z in the upper half-plane, we have
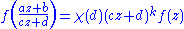
and f is holomorphic at all the cusps
; when the form vanishes at all cusps, it is called a cusp form.
. For each even integer k > 2, we define Ek(Λ) to be the sum of λ−k over all non-zero vectors λ of Λ:
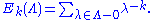
The condition k > 2 is needed for convergence
; the condition that k is even prevents λ−k from cancelling with (−λ)−k.
An even unimodular lattice
L in Rn is a lattice generated by n vectors forming the columns of a matrix of determinant 1 and satisfying the condition that the square of the length of each vector in L is an even integer. As a consequence of the Poisson summation formula
, the theta function
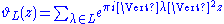
is a modular form of weight n/2. It is not so easy to construct even unimodular lattices, but here is one way: Let n be an integer divisible by 8 and consider all vectors v in Rn such that 2v has integer coordinates, either all even or all odd, and such that the sum of the coordinates of v is an even integer. We call this lattice Ln. When n=8, this is the lattice generated by the roots in the root system
called E8
.
Because there is only one modular form of weight 8 up to scalar multiplication,
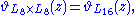
even though the lattices L8×L8 and L16
are not similar. John Milnor
observed that the 16-dimensional tori
obtained by dividing R16 by these two lattices are consequently examples of compact
Riemannian manifold
s which are isospectral
but not isometric
(see Hearing the shape of a drum
.)
The Dedekind eta function
is defined as
Then the modular discriminant Δ(z)=η(z)24 is a modular form of weight 12. The presence of 24
can be connected to the Leech lattice
, which has 24 dimensions. A celebrated conjecture of Ramanujan asserted that the qp coefficient for any prime p has absolute value ≤2p11/2. This was settled by Pierre Deligne
as a result of his work on the Weil conjectures
.
The second and third examples give some hint of the connection between modular forms and classical questions in number theory, such as representation of integers by quadratic form
s and the partition function. The crucial conceptual link between modular forms and number theory are furnished by the
theory of Hecke operator
s, which also gives the link between the theory of modular forms and representation theory
.
s, it is a function Δ(g) determined by the conjugation action.
Maass forms are real-analytic
eigenfunction
s of the Laplacian but need not be holomorphic. The holomorphic parts of certain weak Maass wave forms turn out to be essentially Ramanujan's mock theta function
s. Groups which are not subgroups of SL(2,Z) can be considered.
Hilbert modular forms are functions in n variables, each a complex number in the upper half-plane, satisfying a modular relation for 2×2 matrices with entries in a totally real number field
.
Siegel modular form
s are associated to larger symplectic group
s in the same way in which the forms we have discussed are associated to SL(2,R); in other words, they are related to abelian varieties
in the same sense that our forms (which are sometimes called elliptic modular forms to emphasize the point) are related to elliptic curves.
Jacobi forms are a mixture of modular forms and elliptic functions. Examples of
such functions are very classical - the Jacobi theta functions and the Fourier
coefficients of Siegel modular forms of genus two - but it is a relatively recent
observation that the Jacobi forms have an arithmetic theory very analogous to the
usual theory of modular forms.
Automorphic form
s extend the notion of modular forms to general Lie group
s.
s, in the first part of the nineteenth century; then by Felix Klein
and others towards the end of the nineteenth century as the automorphic form concept became understood (for one variable); then by Erich Hecke
from about 1925; and then in the 1960s, as the needs of number theory and the formulation of the modularity theorem in particular made it clear that modular forms are deeply implicated.
The term modular form, as a systematic description, is usually attributed to Hecke.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a modular form is a (complex) analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
on the upper half-plane satisfying a certain kind of functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
and growth condition. The theory of modular forms therefore belongs to complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
but the main importance of the theory has traditionally been in its connections with number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Modular forms appear in other areas, such as algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
A modular function is a modular form, without the condition that f(z) be holomorphic at infinity. Instead, modular functions are meromorphic at infinity.
Modular form theory is a special case of the more general theory of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s, and therefore can now be seen as just the most concrete part of a rich theory of discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s.
Modular forms for SL2(Z)
A modular form of weight k for the group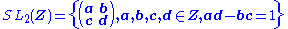is a complex-valued function f on satisfying the following three conditions: firstly, f is a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on H. Secondly, for any z in H and any matrix in SL2(Z) as above, the equation
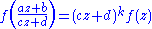
is required to hold. Thirdly, f is required to be holomorphic as
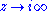. The latter condition is also phrased by saying that f is "holomorphic at the cusp", a terminology that is explained below. The weight k is typically a positive integer.The second condition, with the matrices
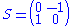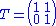and reads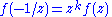and
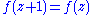
respectively. Since S and T generate the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
SL2(Z), the second condition above is equivalent to these two equations.
Definition in terms of lattices or elliptic curves
A modular form can equivalently be defined as a function F from the set of lattices Λ in C (that is, subgroups of C that are isomorphic to Z2) to the set of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s which satisfies certain conditions:
If we consider the lattice
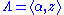generated by a constant α and a variable z, then F(Λ) is an analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of z.
If α is a non-zero complex number and αΛ is the lattice obtained by multiplying each element of Λ by α, then F(αΛ) = α−kF(Λ) where k is a constant (typically a positive integer) called the weight of the form.
The absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of F(Λ) remains bounded above as long as the absolute value of the smallest non-zero element in Λ is bounded away from 0.
The key idea in proving the equivalence of the two definitions is that such a function F is determined, because of the first property, by its values on lattices of the form
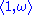, where ω ∈ H.Modular functions
When the weight k is zero, the only modular forms are constant functions, as can be shown. However, relaxing the requirement that f be holomorphic leads to the notion of modular functions. A function f : H → C is called modular iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it satisfies the following properties:
- f is meromorphicMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
in the open upper half-plane H. - For every matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
M in the modular group Γ, f(Mτ) = f(τ). - f is required to be "meromorphic at the cusp". This means the following: as pointed out above, the second condition implies that f is periodic, and therefore has a Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. The third condition is that this series is of the form
It is often written in terms of as
(the square of the nome),
This is also referred to as the q-expansion of f (see also q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
). The coefficients a(n) are known as the Fourier coefficients of f, the number m is called the order of the pole of f at
.Another way to phrase the definition of modular functions is to use elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s: every lattice Λ determines an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
C/Λ over C; two lattices determine isomorphic elliptic curves if and only if one is obtained from the other by multiplying by some non-zero complex number α. Thus, a modular function can also be regarded as a meromorphic function on the set of isomorphism classes of elliptic curves. For example, the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
j(z) of an elliptic curve, regarded as a function on the set of all elliptic curves, is a modular function. More conceptually, modular functions can be thought of as functions on the moduli space of isomorphism classes of complex elliptic curves.
A modular form f that vanishes at
(equivalently, a(0) = 0, also paraphrased as z = i∞) is called a cusp formCusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
(Spitzenform in German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
). The smallest n such that a(n) ≠ 0 is the order of the zero of f at i∞.
Modular forms for more general groups
The functional equation, i.e., the behavior of f with respect to can be relaxed by requiring it only for matrices in smaller groups.The Riemann surface G\H∗
Let G be a subgroup of SL(2, Z) that is of finite indexIndex of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
. Such a group G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on H in the same way as SL(2, Z). The quotient topological space G\H can be shown to be a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Typically it is not compact, but can be compactified by adding a finite number of points called cusps. These are points at the boundary of H, i.e., either in Q, the rationals, or ∞, such that there is a parabolic element of G (a matrix with trace ±2) fixing the point. Here, a matrix
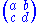sends ∞ to a/c. This yields a compact topological space G\H∗. What is more, it can be endowed with the structure of a Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, which allows to speak of holo- and meromorphic functions.
Important examples are, for any positive integer N, either one of the congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
s
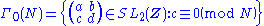
and
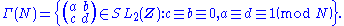
For G = Γ0(N) or Γ(N), the spaces G\H and G\H∗ are denoted Y0(N) and X0(N) and Y(N), X(N), respectively.
The geometry of G\H∗ can be understood by studying fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
s for G, i.e. subsets D ⊂ H such that D intersects each orbit of the G-action on H exactly once and such that the closure of D meets all orbits. For example, the genus
Genus
In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
of G\H∗ can be computed.
Definition
A modular form for G of weight k is a function on H satisfying the above functional equation for all matrices in G, that is holomorphic on H and at all cusps of G. Again, modular forms that vanish at all cusps are called cusp forms for G. The C-vector spaces of modular and cusp forms of weight k are denoted Mk(G) and Sk(G), respectively. Similarly, a meromorphic function on G\H∗ is called a modular function for G. In case G = Γ0(N), they are also referred to as modular/cusp forms and functions of level N. For G = Γ(1) = SL2(Z), this gives back the afore-mentioned definitions.Consequences
The theory of Riemann surfaces can be applied to G\H∗ to obtain further information about modular forms and functions. For example, the spaces Mk(G) and Sk(G) are finite-dimensional, and their dimensions can be computed thanks to the Riemann-Roch theorem in terms of the geometry of the G-action on H. For example,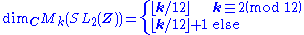where
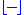denotes the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
The modular functions constitute the field of functions
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
of the Riemann surface, and hence form a field of transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
one (over C). If a modular function f is not identically 0, then it can be shown that the number of zeroes of f is equal to the number of poles of f in the closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of the fundamental region RΓ.It can be shown that the field of modular function of level N (N ≥ 1) is generated by the functions j(z) and j(Nz).
Line bundles
The situation can be profitably compared to that which arises in the search for functions on the projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
P(V): in that setting, one would ideally like functions F on the vector space V which are polynomial in the coordinates of v≠ 0 in V and satisfy the equation F(cv) = F(v) for all non-zero c. Unfortunately, the only such functions are constants. If we allow denominators (rational functions instead of polynomials), we can let F be the ratio of two homogeneous
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
polynomials of the same degree. Alternatively, we can stick with polynomials and loosen the dependence on c, letting F(cv) = ckF(v). The solutions are then the homogeneous polynomials of degree k. On the one hand, these form a finite dimensional vector space for each k, and on the other, if we let k vary, we can find the numerators and denominators for constructing all the rational functions which are really functions on the underlying projective space P(V).
One might ask, since the homogeneous polynomials are not really functions on P(V), what are they, geometrically speaking? The algebro-geometric
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
answer is that they are sections of a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
(one could also say a line bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
in this case). The situation with modular forms is precisely analogous.
Modular forms can also be profitably approached from this geometric direction, as sections of line bundles on the moduli space of elliptic curves.
Entire forms
If f is holomorphic at the cusp (has no pole at), it is called an entire modular form.If f is meromorphic but not holomorphic at the cusp, it is called a non-entire modular form. For example, the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
is a non-entire modular form of weight 0, and has a simple pole at
.Automorphic factors and other generalizations
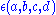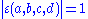Other common generalizations allow the weight k to not be an integer, and allow a multiplier with to appear in the transformation, so that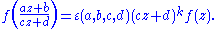Functions of the form
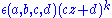are known as automorphic factorAutomorphic factor
In mathematics, an automorphic factor is a certain type of analytic function, defined on subgroups of SL, appearing in the theory of modular forms...
s.
By allowing automorphic factors, functions such as the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
may be encompassed by the theory, being a modular form of weight 1/2. Thus, for example, let
be a Dirichlet characterDirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
mod N. A modular form of weight k, level N (or level group
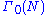) with nebentypus the Dirichlet character is a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
f on the upper half-plane such that for any
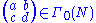
and any z in the upper half-plane, we have
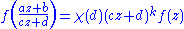
and f is holomorphic at all the cusps
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
; when the form vanishes at all cusps, it is called a cusp form.
Examples
The simplest examples from this point of view are the Eisenstein seriesEisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
. For each even integer k > 2, we define Ek(Λ) to be the sum of λ−k over all non-zero vectors λ of Λ:
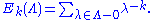
The condition k > 2 is needed for convergence
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
; the condition that k is even prevents λ−k from cancelling with (−λ)−k.
An even unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
L in Rn is a lattice generated by n vectors forming the columns of a matrix of determinant 1 and satisfying the condition that the square of the length of each vector in L is an even integer. As a consequence of the Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
, the theta function
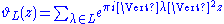
is a modular form of weight n/2. It is not so easy to construct even unimodular lattices, but here is one way: Let n be an integer divisible by 8 and consider all vectors v in Rn such that 2v has integer coordinates, either all even or all odd, and such that the sum of the coordinates of v is an even integer. We call this lattice Ln. When n=8, this is the lattice generated by the roots in the root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
called E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
.
Because there is only one modular form of weight 8 up to scalar multiplication,
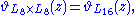
even though the lattices L8×L8 and L16
are not similar. John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
observed that the 16-dimensional tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
obtained by dividing R16 by these two lattices are consequently examples of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s which are isospectral
Isospectral
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
but not isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
(see Hearing the shape of a drum
Hearing the shape of a drum
To hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of basic harmonics, via the use of mathematical theory...
.)
The Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
is defined as
Then the modular discriminant Δ(z)=η(z)24 is a modular form of weight 12. The presence of 24
24 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
can be connected to the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
, which has 24 dimensions. A celebrated conjecture of Ramanujan asserted that the qp coefficient for any prime p has absolute value ≤2p11/2. This was settled by Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
as a result of his work on the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
.
The second and third examples give some hint of the connection between modular forms and classical questions in number theory, such as representation of integers by quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s and the partition function. The crucial conceptual link between modular forms and number theory are furnished by the
theory of Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s, which also gives the link between the theory of modular forms and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
.
Generalizations
There are a number of other usages of the term modular function, apart from this classical one; for example, in the theory of Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
s, it is a function Δ(g) determined by the conjugation action.
Maass forms are real-analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the Laplacian but need not be holomorphic. The holomorphic parts of certain weak Maass wave forms turn out to be essentially Ramanujan's mock theta function
Mock theta function
In mathematics, a mock modular form is the holomorphic part of a harmonic weak Maass form, anda mock theta function is essentially a mock modular form of weight 1/2. The first examples of mock theta functions were described by Srinivasa Ramanujan in his last 1920 letter to G. H. Hardy and in his...
s. Groups which are not subgroups of SL(2,Z) can be considered.
Hilbert modular forms are functions in n variables, each a complex number in the upper half-plane, satisfying a modular relation for 2×2 matrices with entries in a totally real number field
Totally real number field
In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...
.
Siegel modular form
Siegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s are associated to larger symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
s in the same way in which the forms we have discussed are associated to SL(2,R); in other words, they are related to abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
in the same sense that our forms (which are sometimes called elliptic modular forms to emphasize the point) are related to elliptic curves.
Jacobi forms are a mixture of modular forms and elliptic functions. Examples of
such functions are very classical - the Jacobi theta functions and the Fourier
coefficients of Siegel modular forms of genus two - but it is a relatively recent
observation that the Jacobi forms have an arithmetic theory very analogous to the
usual theory of modular forms.
Automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s extend the notion of modular forms to general Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s.
History
The theory of modular forms was developed in three or four periods: first in connection with the theory of elliptic functionElliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s, in the first part of the nineteenth century; then by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
and others towards the end of the nineteenth century as the automorphic form concept became understood (for one variable); then by Erich Hecke
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
from about 1925; and then in the 1960s, as the needs of number theory and the formulation of the modularity theorem in particular made it clear that modular forms are deeply implicated.
The term modular form, as a systematic description, is usually attributed to Hecke.