Relativistic heat conduction
Encyclopedia
The theory of relativistic heat conduction (RHC) claims to be the only model for heat conduction
(and similar diffusion
processes) that is compatible with the theory of special relativity
, the second law of thermodynamics
, electrodynamics, and quantum mechanics
, simultaneously. The main features of RHC are:
These outcomes are achieved by (1) upgrading the Fourier equation
of heat conduction to the form of a Telegraph equation of electrodynamics, and (2) introducing a new definition of the heat flux vector. Consequently, RHC gives rise to a number of interesting phenomena, such as thermal resonance
and thermal shock waves
, which are possible during high-frequency
pulsed laser
heating of thermal insulators
. The main appealing feature of the theory is its mathematical elegance and simplicity.
:
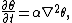
where θ is temperature
, t is time
, α = k/(ρ c) is thermal diffusivity
, k is thermal conductivity
, ρ is density
, and c is specific heat capacity. The Laplace operator
,
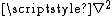, is defined in Cartesian coordinates
as
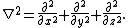
This Fourier equation can be derived by substituting Fourier’s linear approximation of the heat flux vector, q , as a function of temperature gradient,
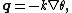
into the first law of thermodynamics
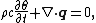
where the del
operator, ∇, is defined in 3D as
It can be shown that this definition of the heat flux vector also satisfies the second law of thermodynamics,
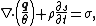
where s is specific entropy
and σ is entropy production. Alternatively, the second law can be written as
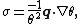
which leads to the condition
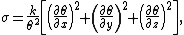
which is always true, because k is a non-negative material property.
) is in contradiction with the theory of relativity, for at least one reason: it admits infinite speed of propagation of heat signals within the continuum field
. For example, consider a pulse of heat at the origin; then according to Fourier equation, it is felt (i.e. temperature changes) at infinity
, instantaneously. The speed of information propagation is faster than the speed of light
in vacuum, which is physically inadmissible within the framework of relativity.
To overcome this contradiction, workers such as Cattaneo, Vernotte, Chester, and others proposed that Fourier equation should be upgraded from the parabolic
to a hyperbolic
form,
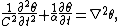
also known as the Telegrapher's equation. Interestingly, the form of this equation traces its origins to Maxwell’s equations of electrodynamics; hence, the wave nature of heat is implied. In this equation, C is called the speed of second sound
(i.e. the fictitious quantum particles, phonons) and this equation is known as the Hyperbolic Heat Conduction (HHC) equation.
For the HHC equation to remain compatible with the first law of thermodynamics, it is necessary to modify the definition of heat flux vector, q, to
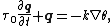
where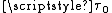
is a relaxation time
, such that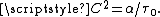
The most important implication of the hyperbolic equation is that by switching from a parabolic (dissipative
) to a hyperbolic (includes a conservative
term) partial differential equation
, there is the possibility of phenomena such as thermal resonance
and thermal shock waves
.
The theory of RHC attempts to resolve the controversies surrounding the hyperbolic equation, while maintaining the form of that equation. This is achieved by:
, distance between any two points, ds, is measured by
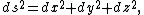
where dx, dy, and dz are displacements along three orthogonal axes.
In a Minkowski space
, distance between two events, ds, is measured by
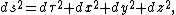
where, τ, is space-like-time and is related to real time, t, by
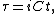
where C is speed of light in vacuum and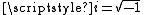
. Hence,
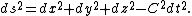
Consequently, the 3D del, ∇,operator is upgraded to the 4D quad,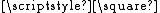
, operator (also known as the Four-gradient
)
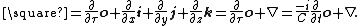
Likewise, the 3D Laplacian,
, operator is upgraded to the 4D d'Alembert operator
,
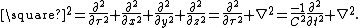
Any physical quantity that is Galilean invariant in Euclidean space can be made Lorentz invariant in a Minkowski space, by upgrading from 3D to 4D operators. Consequently, Fourier’s equation can be upgraded to 4D as
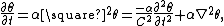
which is called the relativistic heat conduction equation. Likewise, the definition of the heat-flux vector, q, is upgraded to the 4D form as
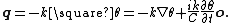
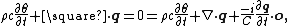
as well as the second law of thermodynamics,
in their 4D upgraded form. The imaginary terms in these equations are direct manifestation of the wave nature of heat, and are essential for the heat equation to become compatible with all laws of physics. The real terms in these equations are identical to those in the classical heat model.
The most interesting observation about RHC is that it reduces the second law of thermodynamics to a statement of the form
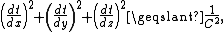
which is the “no action at a distance” principle of special relativity. Essentially, the RHC asserts that relativity and the second law of thermodynamics are two alternative, but equal statements about the nature of time. Both physical principles are mutually derivable from each other and are complementary.
In summary, while the RHC is mathematically simple and elegant, and experimentally practical and relevant, it raises a number of conceptual issues that are highly controversial.
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
(and similar diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
processes) that is compatible with the theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, electrodynamics, and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, simultaneously. The main features of RHC are:
- It admits a finite speedSpeedIn kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
of heatHeatIn physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
propagationWave propagationWave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
, and allows for relativistic effects when heat fluxHeat fluxHeat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
transients approach that speed. - It removes the possibility of paradoxical situations that may violate the second law of thermodynamics.
- It, implicitly, admits the wave–particle dualityWave–particle dualityWave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
of the heat-carrying “phononPhononIn physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
”.
These outcomes are achieved by (1) upgrading the Fourier equation
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
of heat conduction to the form of a Telegraph equation of electrodynamics, and (2) introducing a new definition of the heat flux vector. Consequently, RHC gives rise to a number of interesting phenomena, such as thermal resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
and thermal shock waves
Shock Waves
Shock Waves, , is a 1977 horror movie written and directed by Ken Wiederhorn...
, which are possible during high-frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
pulsed laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
heating of thermal insulators
Thermal insulation
Thermal insulation is the reduction of the effects of the various processes of heat transfer between objects in thermal contact or in range of radiative influence. Heat transfer is the transfer of thermal energy between objects of differing temperature...
. The main appealing feature of the theory is its mathematical elegance and simplicity.
Classical model
For most of the last two centuries, heat conduction has been modelled by the well-known Fourier equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
:
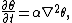
where θ is temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, t is time
Time in physics
Time in physics is defined by its measurement: time is what a clock reads. It is a scalar quantity and, like length, mass, and charge, is usually described as a fundamental quantity. Time can be combined mathematically with other physical quantities to derive other concepts such as motion, kinetic...
, α = k/(ρ c) is thermal diffusivity
Thermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
, k is thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
, ρ is density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, and c is specific heat capacity. The Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
,
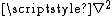, is defined in Cartesian coordinatesCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
as
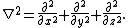
This Fourier equation can be derived by substituting Fourier’s linear approximation of the heat flux vector, q , as a function of temperature gradient,
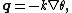
into the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
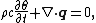
where the del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator, ∇, is defined in 3D as
It can be shown that this definition of the heat flux vector also satisfies the second law of thermodynamics,
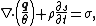
where s is specific entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
and σ is entropy production. Alternatively, the second law can be written as
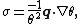
which leads to the condition
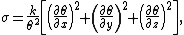
which is always true, because k is a non-negative material property.
Hyperbolic model
For most of the last century, it was recognized that Fourier equation (and its more general Fick's law of diffusionFick's law of diffusion
Fick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
) is in contradiction with the theory of relativity, for at least one reason: it admits infinite speed of propagation of heat signals within the continuum field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
. For example, consider a pulse of heat at the origin; then according to Fourier equation, it is felt (i.e. temperature changes) at infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, instantaneously. The speed of information propagation is faster than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuum, which is physically inadmissible within the framework of relativity.
To overcome this contradiction, workers such as Cattaneo, Vernotte, Chester, and others proposed that Fourier equation should be upgraded from the parabolic
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
to a hyperbolic
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
form,
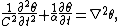
also known as the Telegrapher's equation. Interestingly, the form of this equation traces its origins to Maxwell’s equations of electrodynamics; hence, the wave nature of heat is implied. In this equation, C is called the speed of second sound
Second sound
Second sound is a quantum mechanical phenomenon in which heat transfer occurs by wave-like motion, rather than by the more usual mechanism of diffusion. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity...
(i.e. the fictitious quantum particles, phonons) and this equation is known as the Hyperbolic Heat Conduction (HHC) equation.
For the HHC equation to remain compatible with the first law of thermodynamics, it is necessary to modify the definition of heat flux vector, q, to
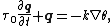
where
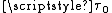is a relaxation timeRelaxation time
In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium.Each relaxation process can be characterized by a relaxation time τ...
, such that
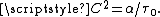
The most important implication of the hyperbolic equation is that by switching from a parabolic (dissipative
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
) to a hyperbolic (includes a conservative
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
term) partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, there is the possibility of phenomena such as thermal resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
and thermal shock waves
Shock Waves
Shock Waves, , is a 1977 horror movie written and directed by Ken Wiederhorn...
.
Criticism to the HHC model
- The relaxation time,
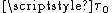, is justified based on microscopicMicroscopicThe microscopic scale is the scale of size or length used to describe objects smaller than those that can easily be seen by the naked eye and which require a lens or microscope to see them clearly.-History:...
aspects of lattice vibrationPhononIn physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
and electron transportTransport PhenomenaTransport Phenomena is the first textbook that is about transport phenomena. It is specifically designed for chemical engineering students...
; is an extension of kinetic theoryKinetic theoryThe kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
calculations and Boltzmann equationBoltzmann equationThe Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
for rarefied gases to the case of solids; and is calculated from statisticalStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
NewtonianClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
mechanics.. Further, the speed C is only a collection of terms, α and
, and has no physical reality or significance similar to that associated with the speed of light. Hence, the hyperbolic equation is compatible with relativity artificially (in form only), but is still fundamentally classical Newtonian. - The new definition of heat flux vector is an ad hoc mathematical approximation of a far more complicated expression; this raises some doubts about the whole approach.
- The most serious criticism is that the hyperbolic equation can violate the second law of thermodynamics. For example, consider an infinitely long wire conductor, with a heat source at the origin, and measure temperature at distances significantly remote from origin. If the heat source at origin varies with a frequency much higher than the relaxation time (i.e. faster than the speed of second sound) then the hyperbolic equation admits a temperature field in which heat would appear to be moving from cold to hot, in violation of the second law. This contradiction was demonstrated in more mathematically rigorous form.
The theory of RHC attempts to resolve the controversies surrounding the hyperbolic equation, while maintaining the form of that equation. This is achieved by:
- Deriving the hyperbolic equation starting from space-time duality of a Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, and simple Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s, that are basic to the theory of special relativity. This is done without any reference to microstructureMicrostructureMicrostructure is defined as the structure of a prepared surface or thin foil of material as revealed by a microscope above 25× magnification...
or statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. - Treating the speed of second sound, C, as a fundamental property of the temperature field, although still fundamentally inferior to the speed of light.
- Modifying the definition of the heat flux vector so that it is simpler, more elegant, and bring it in compliance with the second law of thermodynamics.
Transformations
In a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, distance between any two points, ds, is measured by
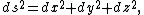
where dx, dy, and dz are displacements along three orthogonal axes.
In a Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, distance between two events, ds, is measured by
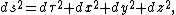
where, τ, is space-like-time and is related to real time, t, by
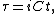
where C is speed of light in vacuum and
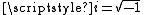. Hence,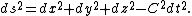Consequently, the 3D del, ∇,operator is upgraded to the 4D quad,
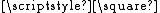, operator (also known as the Four-gradientFour-gradient
The four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
)
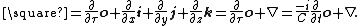
Likewise, the 3D Laplacian,
, operator is upgraded to the 4D d'Alembert operatorD'Alembert operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
,
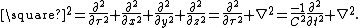
Any physical quantity that is Galilean invariant in Euclidean space can be made Lorentz invariant in a Minkowski space, by upgrading from 3D to 4D operators. Consequently, Fourier’s equation can be upgraded to 4D as
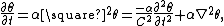
which is called the relativistic heat conduction equation. Likewise, the definition of the heat-flux vector, q, is upgraded to the 4D form as
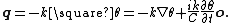
Implications
It can be shown that this definition of q is compatible with the first law of thermodynamics,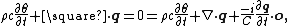as well as the second law of thermodynamics,
in their 4D upgraded form. The imaginary terms in these equations are direct manifestation of the wave nature of heat, and are essential for the heat equation to become compatible with all laws of physics. The real terms in these equations are identical to those in the classical heat model.
The most interesting observation about RHC is that it reduces the second law of thermodynamics to a statement of the form
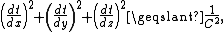
which is the “no action at a distance” principle of special relativity. Essentially, the RHC asserts that relativity and the second law of thermodynamics are two alternative, but equal statements about the nature of time. Both physical principles are mutually derivable from each other and are complementary.
Criticism to RHC
As far as heat conduction is concerned, the RHC equation is identical in form to the hyperbolic equation, and all analytical and experimental results that are relevant to one are equally applicable to the other. The definition of heat flux vector, however, is different; but the RHC definition is merely a 4D upgrade of the original linear Fourier approximation. The mathematics of RHC is much simpler and more elegant. However, RHC raises some significant conceptual challenges:- This weak interpretation of relativity, in which the speed of second sound plays a role similar to that of the speed of light, can be viewed as downgrading or degrading to the universality of the theory of relativity. Notice how the symbol c in standard relativity theory is replaced with C without much interpretation.
- The implied wave nature of heat is controversial. Some workers reject the wave nature of heat on dogmatic grounds. Moreover, RHC implies that a phonon is a full-fledged objective quantum particle whose physical reality is no lesser than that of a photon. Existing experimental evidences are not enough to support for or against such views.
- Heat quantities become complex numbers, with values including "imaginary temperature", which are hard to interpret experimentally.
- The equivalence of relativity and the second law is shocking, because it implies that one of them can be a derivative of the other.
In summary, while the RHC is mathematically simple and elegant, and experimentally practical and relevant, it raises a number of conceptual issues that are highly controversial.