
Hyperboloid model
Encyclopedia
In geometry
, the hyperboloid model, also known as the Minkowski model or the Lorentz model (after Hermann Minkowski
and Hendrik Lorentz
), is a model of n-dimensional hyperbolic geometry
in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space
and m-planes are represented by the intersections of the (m+1)-planes in Minkowski space with S+. The hyperbolic distance function admits a simple expression in this model. The hyperboloid model of the n-dimensional hyperbolic space is closely related to the Beltrami–Klein model: both are projective models in the sense that the isometry group
is a subgroup of the projective group.
is defined to be
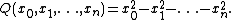
The vectors v∈ Rn+1 such that Q(v) = 1 form an n-dimensional hyperboloid S consisting of two connected component
s, or sheets: the forward, or future, sheet S+, where x0>0 and the backward, or past, sheet S−, where x0<0. The points of the n-dimensional hyperboloid model are the points on the forward sheet S+.
The Minkowski bilinear form B is the polarization
of the Minkowski quadratic form Q,
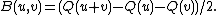
Explicitly,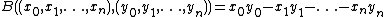 .
.
The hyperbolic distance between two points u and v of S+ is given by the formula
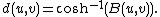
(n+1)-dimensional Lorentz group
, is the Lie group
of real
(n+1)×(n+1) matrices
which preserve the Minkowski bilinear form. In a different language, it is
the group of linear isometries
of the Minkowski space
. In particular, this group preserves the hyperboloid S. The subgroup of O(1,n) which preserves the sign of the first coordinate is the orthochronous Lorentz group, denoted O+(1,n). Its subgroup SO+(1,n) consisting of matrices with determinant
one is a connected Lie group of dimension n(n+1)/2 which acts on S+ by linear automorphisms and preserves the hyperbolic distance. This action is transitive and the stabilizer of the vector (1,0,…,0) consists of the matrices of the form
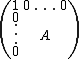
Where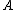 belongs to the compact special orthogonal group SO(n) (generalizing the rotation group
belongs to the compact special orthogonal group SO(n) (generalizing the rotation group
for n=3). It follows that the n-dimensional hyperbolic space
can be exhibited as the homogeneous space
and a Riemannian symmetric space
of rank 1,
In fact, the group SO+(1,n) is the full group of orientation-preserving isometries of the n-dimensional hyperbolic space.
published "Die Rechnung in Nicht-Euclidischen Raumformen" in Crelle's Journal
(89:265–87). This work discusses the hyperboloid model in a way that shows the analogy to the hemisphere model. Killing attributes the idea to Karl Weierstrass
in a Berlin seminar some years before. Following on Killing’s attribution, the phrase Weierstrass coordinates has been associated with elements of the hyperboloid model as follows:
Given an inner product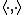 on Rn,
on Rn,
the Weierstrass coordinates of x ∈ Rn are: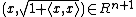 compared to
compared to 
for the hemispherical model. (See Elena Deza and Michel Deza
(2006) Dictionary of Distances.)
According to Jeremy Gray (1986), Poincaré
used the hyperboloid model in his personal notes in 1880. Gray shows where the hyperboloid model is implicit in later writing by Poincaré.
For his part, W. Killing continued to publish on the hyperboloid model, particularly in 1885 in his Analytic treatment of non-Euclidean spaceforms. Further exposure of the model was given by Alfred Clebsch
and Ferdinand Lindemann in 1891 in Vorlesungen uber Geometrie, page 524.
The hyperboloid was explored as a metric space
by Alexander Macfarlane
in his Papers in Space Analysis (1894). He noted that points on the hyperboloid could be written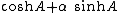
where α is a basis vector orthogonal to the hyperboloid axis. For example, he obtained the hyperbolic law of cosines through use of his
Algebra of Physics
.
H. Jansen made the hyperboloid model the explicit focus of his 1909 paper "Representation of hyperbolic geometry on a two sheeted hyperboloid".
In 1993 W.F. Reynolds recounted some of the early history of the model in his article in the American Mathematical Monthly
.
Being a commonplace model by the twentieth century, it was identified with the Geschwindigkeitsvectoren (velocity vectors) by Hermann Minkowski
in his Minkowski space
of 1908. Scott Walter, in his 1999 paper "The Non-Euclidean Style of Special Relativity" recalls Minkowski’s awareness, but traces the lineage of the model to Hermann Helmholtz rather than Weierstrass and Killing. In the early years of relativity the hyperboloid model was used by Vladimir Varićak
to explain the physics of velocity. In his speech to the German mathematical union in 1912 he referred to Weierstrass coordinates.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the hyperboloid model, also known as the Minkowski model or the Lorentz model (after Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
and Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
), is a model of n-dimensional hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
and m-planes are represented by the intersections of the (m+1)-planes in Minkowski space with S+. The hyperbolic distance function admits a simple expression in this model. The hyperboloid model of the n-dimensional hyperbolic space is closely related to the Beltrami–Klein model: both are projective models in the sense that the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
is a subgroup of the projective group.
Minkowski quadratic form
If (x0, x1, …, xn) is a vector in the (n+1)-dimensional coordinate space Rn+1, the Minkowski quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
is defined to be
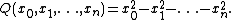
The vectors v∈ Rn+1 such that Q(v) = 1 form an n-dimensional hyperboloid S consisting of two connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s, or sheets: the forward, or future, sheet S+, where x0>0 and the backward, or past, sheet S−, where x0<0. The points of the n-dimensional hyperboloid model are the points on the forward sheet S+.
The Minkowski bilinear form B is the polarization
Polarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
of the Minkowski quadratic form Q,
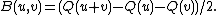
Explicitly,
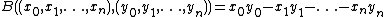 .
.The hyperbolic distance between two points u and v of S+ is given by the formula
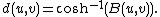
Isometries
The indefinite orthogonal group O(1,n), also called the(n+1)-dimensional Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, is the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(n+1)×(n+1) matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which preserve the Minkowski bilinear form. In a different language, it is
the group of linear isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. In particular, this group preserves the hyperboloid S. The subgroup of O(1,n) which preserves the sign of the first coordinate is the orthochronous Lorentz group, denoted O+(1,n). Its subgroup SO+(1,n) consisting of matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
one is a connected Lie group of dimension n(n+1)/2 which acts on S+ by linear automorphisms and preserves the hyperbolic distance. This action is transitive and the stabilizer of the vector (1,0,…,0) consists of the matrices of the form
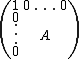
Where
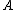 belongs to the compact special orthogonal group SO(n) (generalizing the rotation group
belongs to the compact special orthogonal group SO(n) (generalizing the rotation groupRotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
for n=3). It follows that the n-dimensional hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
can be exhibited as the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
and a Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
of rank 1,
In fact, the group SO+(1,n) is the full group of orientation-preserving isometries of the n-dimensional hyperbolic space.
History
In 1880 Wilhelm KillingWilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
published "Die Rechnung in Nicht-Euclidischen Raumformen" in Crelle's Journal
Crelle's Journal
Crelle's Journal, or just Crelle, is the common name for a mathematics journal, the Journal für die reine und angewandte Mathematik .- History :...
(89:265–87). This work discusses the hyperboloid model in a way that shows the analogy to the hemisphere model. Killing attributes the idea to Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
in a Berlin seminar some years before. Following on Killing’s attribution, the phrase Weierstrass coordinates has been associated with elements of the hyperboloid model as follows:
Given an inner product
 on Rn,
on Rn,the Weierstrass coordinates of x ∈ Rn are:
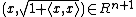 compared to
compared to 
for the hemispherical model. (See Elena Deza and Michel Deza
Michel Deza
Michel Marie Deza is a Soviet and French mathematician, specializing in combinatorics, discrete geometry and graph theory...
(2006) Dictionary of Distances.)
According to Jeremy Gray (1986), Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
used the hyperboloid model in his personal notes in 1880. Gray shows where the hyperboloid model is implicit in later writing by Poincaré.
For his part, W. Killing continued to publish on the hyperboloid model, particularly in 1885 in his Analytic treatment of non-Euclidean spaceforms. Further exposure of the model was given by Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
and Ferdinand Lindemann in 1891 in Vorlesungen uber Geometrie, page 524.
The hyperboloid was explored as a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
by Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
in his Papers in Space Analysis (1894). He noted that points on the hyperboloid could be written
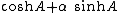
where α is a basis vector orthogonal to the hyperboloid axis. For example, he obtained the hyperbolic law of cosines through use of his
Algebra of Physics
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
.
H. Jansen made the hyperboloid model the explicit focus of his 1909 paper "Representation of hyperbolic geometry on a two sheeted hyperboloid".
In 1993 W.F. Reynolds recounted some of the early history of the model in his article in the American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
.
Being a commonplace model by the twentieth century, it was identified with the Geschwindigkeitsvectoren (velocity vectors) by Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
in his Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
of 1908. Scott Walter, in his 1999 paper "The Non-Euclidean Style of Special Relativity" recalls Minkowski’s awareness, but traces the lineage of the model to Hermann Helmholtz rather than Weierstrass and Killing. In the early years of relativity the hyperboloid model was used by Vladimir Varićak
Vladimir Varicak
Vladimir Varićak was a Croatian mathematician and theoretical physicist of Serbian descent....
to explain the physics of velocity. In his speech to the German mathematical union in 1912 he referred to Weierstrass coordinates.


