Minkowski diagram
Encyclopedia
The Minkowski diagram was developed in 1908 by Hermann Minkowski
and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation
and length contraction
without mathematical equations.
The term Minkowski diagram is used in both a generic and particular sense. In general, a Minkowski diagram is a graphic depiction of a portion of Minkowski space
, often where space has been curtailed to a single dimension. These two-dimensional diagrams portray worldlines as curves in a plane that correspond to motion along the spatial axis. The vertical axis is usually temporal, and the units of measurement
are taken such that the light cone
at an event consists of the lines of slope
plus or minus one through that event.
A particular Minkowski diagram illustrates the result of a Lorentz transformation
. The origin corresponds to an event where a change of velocity
takes place. The new worldline forms an angle α with the vertical, with α < π/4. The Lorentz transformation that moves the vertical to α also moves the horizontal by α. The horizontal corresponds to the usual notion of simultaneous events, for a stationary observer at the origin. After the Lorentz transformation the new simultaneous events lie on the α-inclined line. Whatever the magnitude of α, the line t = x forms the universal bisector.
In Minkowski’s 1908 paper there were three diagrams, first to illustrate the Lorentz transformation, then the partition of the plane by the light-cone, and finally illustration of worldlines. The first diagram used a branch of the unit hyperbola
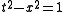to show the locus of a unit of proper time
depending on velocity, thus illustrating time dilation. The second diagram showed the conjugate hyperbola to calibrate space, where a similar stretching leaves the impression of Fitzgerald contraction. In 1914 Ludwik Silberstein
included a diagram of "Minkowski’s representation of the Lorentz transformation". This diagram included the unit hyperbola, its conjugate, and a pair of conjugate diameters
. Since the 1960s a version of this more complete configuration has been referred to as The Minkowski Diagram, and used as a standard illustration of the transformation geometry
of special relativity. E. T. Whittaker
has pointed out that the Principle of relativity
is tantamount to the arbitrariness of what hyperbola radius is selected for time
in the Minkowski diagram. In 1912 Gilbert N. Lewis
and Edwin B. Wilson applied the methods of synthetic geometry
to develop the properties of the non-Euclidean plane that has Minkowski diagrams.
) and the time on the y-axis (ordinate
). In this manner the events happening on a horizontal path in reality can be transferred easily to a horizontal line in the diagram. Objects plotted on the diagram can be thought of as moving from bottom to top as time passes. In this way each object, like an observer or a vehicle, follows in the diagram a certain curve which is called its world line
.
Each point in the diagram represents a certain position in space and time. Such a position is called an event whether or not anything happens at that position.
For convenience, the (vertical) time axis represents, not t, but the corresponding quantity ct, where c =299,792,458 m/s is the speed of light. In this way, one second
on the ordinate corresponds to a distance of 299,792,458 m on the abscissa. Due to x=ct for a photon
passing through the origin
to the right, its world line is a straight line with a slope of 45°, if the scales on both axes are chosen to be identical.
This blue line can be interpreted as the time axis for the second observer. Together with the path axis (which is identical for both observers) it represents his coordinate system. This corresponds with the agreement between both observers to denote the position x=0 and t=0 also with x' =0 and t' =0. The axes for the moving observer are not perpendicular
to each other and the scale on his time axis is stretched. To determine the coordinates of a certain event, two lines parallel to the two axes must be constructed passing through the event, and their intersections with the axes read off.
Determining position and time of the event A as an example in the diagram leads to the same time for both observers, as expected. Only for the position different values result, because the moving observer has approached the position of the event A since t=0. Generally stated, all events on a line parallel to the path axis happen simultaneously for both observers. There is only one universal time t=t' which corresponds with the existence of only one common path axis. On the other hand due to two different time axes the observers usually measure different path coordinates for the same event. This graphical translation from x and t to x' and t' and vice versa is described mathematically by the so called Galilean transformation
.
discovered that the description above is not correct. Space and time have properties which lead to different rules for the translation of coordinates in case of moving observers. In particular, events which are estimated to happen simultaneously from the viewpoint of one observer, happen at different times for the other.
In the Minkowski diagram this relativity of simultaneity
corresponds with the introduction of a separate path axis for the moving observer. Following the rule described above each observer interprets all events on a line parallel to his path axis as simultaneous. The sequence of events from the viewpoint of an observer can be illustrated graphically by shifting this line in the diagram from bottom to top.
If ct instead of t is assigned on the time axes, the angle α between both path axes will be identical with that between both time axes. This follows from the second postulate of the special relativity, saying that the speed of light is the same for all observers, regardless of their relative motion (see below). α is given by
.
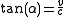The corresponding translation from x and t to x' and t' and vice versa is described mathematically by the so called Lorentz transformation
. Whatever space and time axes arise through such transformation, in a Minkowski diagram they correspond to conjugate diameters
of a pair of hyperbola
s.
For the graphical translation it has been taken into account that the scales on the inclined axes are different from the Newtonian case described above. To avoid this problem it is recommended that the whole diagram be deformed in such a way that the scales become identical for all axes, eliminating any need to stretch or compress either axis. This can be done by a compression in the direction of 45° or an expansion in the direction of 135° until the angle between the time axes becomes equal to the angle between the path axes. The angle β between both time and path axes is given by
.
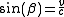In this symmetrical representation (also referred to as Loedel diagram, named after the physicist Enrique Loedel Palumbo
who first introduced this symmetrised Minkowski representation), the coordinate systems of both observers are equivalent, since both observers are traveling at the same speed in opposite directions, relative to some third point of view.
However, Loedel diagrams become more complicated than Minkowski diagrams for more than three observers and therefore lose their pedagogical appeal.
A second observer having moved together with the clock from O to B will argue that the other clock has reached only C until this moment and therefore this clock runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity the question of "who is right" has no answer and does not make sense.
' -axis and the parallel line passing through A and B. For this observer the endpoints of the object at t=0 are O and A. For a second observer moving together with the object, so that for him the object is at rest, it has the length OB at t' =0. Due to OA
The second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the ct-axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the times at which these events happen actually from their point of view.
For world lines of photons passing the origin in different directions x=ct and x=−ct holds. That means any position on such a world line corresponds with steps on x- and ct-axis of equal absolute value. From the rule for reading off coordinates in coordinate system with tilted axes follows that the two world lines are the angle bisectors of the x- and ct-axis. The Minkowski diagram shows, that they are angle bisectors of the x'- and ct'-axis as well. That means both observers measure the same speed c for both photons.
In principle further coordinate systems corresponding to observers with arbitrary velocities can be added in this Minkowski diagram. For all these systems both photon world lines represent the angle bisectors of the axes. The more the relative speed approaches the speed of light the more the axes approach the corresponding angle bisector. The path axis is always more flat and the time axis more steep than the photon world lines. The scales on both axes are always identical, but usually different from those of the other coordinate systems.
Following the same argument the range below the origin and between the photon world lines is the absolute past relative to the origin. Any event there belongs definitely to the past and can be the cause of an effect at the origin.
The relationship between of such pairs of event is called timelike, because they have a finite time distance different from zero for all observers. On the other hand a straight line connecting these two events is always the time axis of a possible observer for whom they happen at the same place. Two events which can be connected just with the speed of light are called lightlike.
In principle a further dimension of space can be added to the Minkowski diagram leading to a three-dimensional representation. In this case the ranges of future and past become cone
s with apexes touching each other at the origin. They are called light cones.
regardless of the speed of the observer. Therefore no event outside the light cones can be reached from the origin, even by a light-signal, nor by any object or signal moving with less than the speed of light. Such pairs of events are called spacelike because they have a finite spatial distance different from zero for all observers. On the other hand a straight line connecting such events is always the space coordinate axis of a possible observer for whom they happen at the same time. By a slight variation of the velocity of this coordinate system in both directions it is always possible to find two inertial reference frames whose observers estimate the chronological order of these events to be different.
Therefore an object moving faster than light, say from O to A in the adjoining diagram, would imply that, for any observer watching the object moving from O to A, there can be found another observer (moving at less than the speed of light with respect to the first) for whom the object moves from A to O. The question of which observer is right has no unique answer, and therefore makes no physical sense. Any such moving object or signal would violate the principle of causality.
Also, any general technical means of sending signals faster than light would permit information to be sent into the originator's own past. In the diagram, an observer at O in the x-ct-system sends a message moving faster than light to A. At A it is received by another observer, moving so as to be in the x'-ct'-system, who sends it back, again faster than light by the same technology, arriving at B. But B is in the past relative to O. The absurdity of this process becomes obvious when both observers subsequently confirm that they received no message at all but all messages were directed towards the other observer as can be seen graphically in the Minkowski diagram. Indeed, if it was possible to accelerate an observer to the speed of light, the space and time axes would coincide with their angle bisector. The coordinate system would collapse.
These considerations show that the speed of light as a limit is a consequence of the properties of space and time, and not of the properties of objects such as technologically imperfect space ships. The prohibition of faster-than-light motion actually has nothing in particular to do with electromagnetic waves or light (applying also to eg gravitational wave
s), but depends on the structure of spacetime and our notion of causality, which such motions appear to violate.
As an eponym
, the term Minkowski diagram is subject to Stigler’s law of eponymy, namely that Minkowski is wrongly designated as originator. The earlier works of Alexander Macfarlane
contain algebra and diagrams that correspond well with the Minkowski diagram. See for instance the plate of figures in Proceedings of the Royal Society in Edinburgh for 1900. Macfarlane was building on what one sees in William Kingdon Clifford
’s Elements of Dynamic (1878), page 90.
When abstracted to a line drawing, then any figure showing conjugate hyperbolas, with a selection of conjugate diameters, falls into this category. Students making drawings to accompany the exercises in George Salmon
’s A Treatise on Conic Sections (1900) at pages 165–71 (on conjugate diameters) will be making Minkowski diagrams.
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation
Time dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
and length contraction
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
without mathematical equations.
The term Minkowski diagram is used in both a generic and particular sense. In general, a Minkowski diagram is a graphic depiction of a portion of Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, often where space has been curtailed to a single dimension. These two-dimensional diagrams portray worldlines as curves in a plane that correspond to motion along the spatial axis. The vertical axis is usually temporal, and the units of measurement
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
are taken such that the light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
at an event consists of the lines of slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
plus or minus one through that event.
A particular Minkowski diagram illustrates the result of a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
. The origin corresponds to an event where a change of velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
takes place. The new worldline forms an angle α with the vertical, with α < π/4. The Lorentz transformation that moves the vertical to α also moves the horizontal by α. The horizontal corresponds to the usual notion of simultaneous events, for a stationary observer at the origin. After the Lorentz transformation the new simultaneous events lie on the α-inclined line. Whatever the magnitude of α, the line t = x forms the universal bisector.
In Minkowski’s 1908 paper there were three diagrams, first to illustrate the Lorentz transformation, then the partition of the plane by the light-cone, and finally illustration of worldlines. The first diagram used a branch of the unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
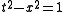to show the locus of a unit of proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
depending on velocity, thus illustrating time dilation. The second diagram showed the conjugate hyperbola to calibrate space, where a similar stretching leaves the impression of Fitzgerald contraction. In 1914 Ludwik Silberstein
Ludwik Silberstein
Ludwik Silberstein was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework...
included a diagram of "Minkowski’s representation of the Lorentz transformation". This diagram included the unit hyperbola, its conjugate, and a pair of conjugate diameters
Conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter...
. Since the 1960s a version of this more complete configuration has been referred to as The Minkowski Diagram, and used as a standard illustration of the transformation geometry
Transformation geometry
In mathematics, transformation geometry is a name for a pedagogic theory for teaching Euclidean geometry, based on the Erlangen programme. Felix Klein, who pioneered this point of view, was himself interested in mathematical education. It took many years, though, for his "modern" point of view to...
of special relativity. E. T. Whittaker
E. T. Whittaker
Edmund Taylor Whittaker FRS FRSE was an English mathematician who contributed widely to applied mathematics, mathematical physics and the theory of special functions. He had a particular interest in numerical analysis, but also worked on celestial mechanics and the history of physics...
has pointed out that the Principle of relativity
Principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
is tantamount to the arbitrariness of what hyperbola radius is selected for time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
in the Minkowski diagram. In 1912 Gilbert N. Lewis
Gilbert N. Lewis
Gilbert Newton Lewis was an American physical chemist known for the discovery of the covalent bond , his purification of heavy water, his reformulation of chemical thermodynamics in a mathematically rigorous manner accessible to ordinary chemists, his theory of Lewis acids and...
and Edwin B. Wilson applied the methods of synthetic geometry
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
to develop the properties of the non-Euclidean plane that has Minkowski diagrams.
Basics
For simplification in Minkowski diagrams, usually only events in a one dimensional world are considered. Unlike common distance-time diagrams, the distance will be displayed on the x-axis (abscissaAbscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
) and the time on the y-axis (ordinate
Ordinate
In mathematics, ordinate refers to that element of an ordered pair which is plotted on the vertical axis of a two-dimensional Cartesian coordinate system, as opposed to the abscissa...
). In this manner the events happening on a horizontal path in reality can be transferred easily to a horizontal line in the diagram. Objects plotted on the diagram can be thought of as moving from bottom to top as time passes. In this way each object, like an observer or a vehicle, follows in the diagram a certain curve which is called its world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
.
Each point in the diagram represents a certain position in space and time. Such a position is called an event whether or not anything happens at that position.
For convenience, the (vertical) time axis represents, not t, but the corresponding quantity ct, where c =299,792,458 m/s is the speed of light. In this way, one second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
on the ordinate corresponds to a distance of 299,792,458 m on the abscissa. Due to x=ct for a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
passing through the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
to the right, its world line is a straight line with a slope of 45°, if the scales on both axes are chosen to be identical.
Path-time diagram in Newtonian physics
The adjoining diagram shows the coordinate system of an observer which we will refer to as 'at rest', and who is positioned at x=0. His world line is identical with the time axis. Each parallel line to this axis would correspond also to an object at rest but at another position. The blue line, however, describes an object moving with constant speed v to the right, such as a moving observer.This blue line can be interpreted as the time axis for the second observer. Together with the path axis (which is identical for both observers) it represents his coordinate system. This corresponds with the agreement between both observers to denote the position x=0 and t=0 also with x
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to each other and the scale on his time axis is stretched. To determine the coordinates of a certain event, two lines parallel to the two axes must be constructed passing through the event, and their intersections with the axes read off.
Determining position and time of the event A as an example in the diagram leads to the same time for both observers, as expected. Only for the position different values result, because the moving observer has approached the position of the event A since t=0. Generally stated, all events on a line parallel to the path axis happen simultaneously for both observers. There is only one universal time t=t
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
.
Minkowski diagram in special relativity
Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
discovered that the description above is not correct. Space and time have properties which lead to different rules for the translation of coordinates in case of moving observers. In particular, events which are estimated to happen simultaneously from the viewpoint of one observer, happen at different times for the other.
In the Minkowski diagram this relativity of simultaneity
Relativity of simultaneity
In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
corresponds with the introduction of a separate path axis for the moving observer. Following the rule described above each observer interprets all events on a line parallel to his path axis as simultaneous. The sequence of events from the viewpoint of an observer can be illustrated graphically by shifting this line in the diagram from bottom to top.
If ct instead of t is assigned on the time axes, the angle α between both path axes will be identical with that between both time axes. This follows from the second postulate of the special relativity, saying that the speed of light is the same for all observers, regardless of their relative motion (see below). α is given by
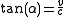.The corresponding translation from x and t to x
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
. Whatever space and time axes arise through such transformation, in a Minkowski diagram they correspond to conjugate diameters
Conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter...
of a pair of hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s.
For the graphical translation it has been taken into account that the scales on the inclined axes are different from the Newtonian case described above. To avoid this problem it is recommended that the whole diagram be deformed in such a way that the scales become identical for all axes, eliminating any need to stretch or compress either axis. This can be done by a compression in the direction of 45° or an expansion in the direction of 135° until the angle between the time axes becomes equal to the angle between the path axes. The angle β between both time and path axes is given by
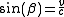.In this symmetrical representation (also referred to as Loedel diagram, named after the physicist Enrique Loedel Palumbo
Enrique Loedel Palumbo
Enrique Loedel Palumbo was a Latin American physicist.Loedel Palumbo was born in Montevideo, Uruguay and studied at the University of La Plata in Argentina. He wrote his Ph.D. thesis on optical and electrical constants of sugar cane...
who first introduced this symmetrised Minkowski representation), the coordinate systems of both observers are equivalent, since both observers are traveling at the same speed in opposite directions, relative to some third point of view.
However, Loedel diagrams become more complicated than Minkowski diagrams for more than three observers and therefore lose their pedagogical appeal.
Time dilation
Relativistic time dilation means that a clock moving relative to an observer is running slower and finally also the time itself in this system. This can be read immediately from the adjoining Minkowski diagram. The observer at A is assumed to move from the origin O towards A and the clock from O to B. For this observer at A all events happening simultaneously in this moment are located on a straight line parallel to its path axis passing A and B. Due to OBA second observer having moved together with the clock from O to B will argue that the other clock has reached only C until this moment and therefore this clock runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity the question of "who is right" has no answer and does not make sense.
Length contraction
Relativistic length contraction means that the length of an object moving relative to an observer is decreased and finally also the space itself is contracted in this system. The observer is assumed again to move along the ct-axis. The world lines of the endpoints of an object moving relative to him are assumed to move along the ctThe second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the ct-axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the times at which these events happen actually from their point of view.
Constancy of the speed of light
Another postulate of special relativity is the constancy of the speed of light. It says that any observer in an inertial reference frame measuring the speed of light relative to himself obtains the same value regardless of his own motion and that of the light source. This statement seems to be paradox, but it follows immediately from the differential equation yielding this, and the Minkowski diagram agrees. It explains also the result of the Michelson–Morley experiment which was considered to be a mystery before the theory of relativity was discovered, when photons were thought to be waves through an undetectable medium.For world lines of photons passing the origin in different directions x=ct and x=−ct holds. That means any position on such a world line corresponds with steps on x- and ct-axis of equal absolute value. From the rule for reading off coordinates in coordinate system with tilted axes follows that the two world lines are the angle bisectors of the x- and ct-axis. The Minkowski diagram shows, that they are angle bisectors of the x'- and ct'-axis as well. That means both observers measure the same speed c for both photons.
In principle further coordinate systems corresponding to observers with arbitrary velocities can be added in this Minkowski diagram. For all these systems both photon world lines represent the angle bisectors of the axes. The more the relative speed approaches the speed of light the more the axes approach the corresponding angle bisector. The path axis is always more flat and the time axis more steep than the photon world lines. The scales on both axes are always identical, but usually different from those of the other coordinate systems.
Speed of light and causality
Straight lines passing the origin which are steeper than both photon world lines correspond with objects moving more slowly than the speed of light. If this applies to an object, then it applies from the viewpoint of all observers, because the world lines of these photons are the angle bisectors for any inertial reference frame. Therefore any point above the origin and between the world lines of both photons can be reached with a speed smaller than that of the light and can have a cause-effect-relationship with the origin. This area is the absolute future, because any event there happens later compared to the event represented by the origin regardless of the observer, which is obvious graphically from the Minkowski diagram.Following the same argument the range below the origin and between the photon world lines is the absolute past relative to the origin. Any event there belongs definitely to the past and can be the cause of an effect at the origin.
The relationship between of such pairs of event is called timelike, because they have a finite time distance different from zero for all observers. On the other hand a straight line connecting these two events is always the time axis of a possible observer for whom they happen at the same place. Two events which can be connected just with the speed of light are called lightlike.
In principle a further dimension of space can be added to the Minkowski diagram leading to a three-dimensional representation. In this case the ranges of future and past become cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
s with apexes touching each other at the origin. They are called light cones.
The speed of light as a limit
Following the same argument, all straight lines passing through the origin and which are more nearly horizontal than the photon world lines, would correspond to objects or signals moving faster than lightFaster-than-light
Faster-than-light communications and travel refer to the propagation of information or matter faster than the speed of light....
regardless of the speed of the observer. Therefore no event outside the light cones can be reached from the origin, even by a light-signal, nor by any object or signal moving with less than the speed of light. Such pairs of events are called spacelike because they have a finite spatial distance different from zero for all observers. On the other hand a straight line connecting such events is always the space coordinate axis of a possible observer for whom they happen at the same time. By a slight variation of the velocity of this coordinate system in both directions it is always possible to find two inertial reference frames whose observers estimate the chronological order of these events to be different.
Therefore an object moving faster than light, say from O to A in the adjoining diagram, would imply that, for any observer watching the object moving from O to A, there can be found another observer (moving at less than the speed of light with respect to the first) for whom the object moves from A to O. The question of which observer is right has no unique answer, and therefore makes no physical sense. Any such moving object or signal would violate the principle of causality.
Also, any general technical means of sending signals faster than light would permit information to be sent into the originator's own past. In the diagram, an observer at O in the x-ct-system sends a message moving faster than light to A. At A it is received by another observer, moving so as to be in the x'-ct'-system, who sends it back, again faster than light by the same technology, arriving at B. But B is in the past relative to O. The absurdity of this process becomes obvious when both observers subsequently confirm that they received no message at all but all messages were directed towards the other observer as can be seen graphically in the Minkowski diagram. Indeed, if it was possible to accelerate an observer to the speed of light, the space and time axes would coincide with their angle bisector. The coordinate system would collapse.
These considerations show that the speed of light as a limit is a consequence of the properties of space and time, and not of the properties of objects such as technologically imperfect space ships. The prohibition of faster-than-light motion actually has nothing in particular to do with electromagnetic waves or light (applying also to eg gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s), but depends on the structure of spacetime and our notion of causality, which such motions appear to violate.
Eponym
When Taylor and Wheeler composed Spacetime Physics (1966), they did not use the term "Minkowski diagram" for their spacetime geometry. Instead they included an acknowledgement of Minkowski’s contribution to philosophy by the totality of his innovation of 1908.As an eponym
Eponym
An eponym is the name of a person or thing, whether real or fictitious, after which a particular place, tribe, era, discovery, or other item is named or thought to be named...
, the term Minkowski diagram is subject to Stigler’s law of eponymy, namely that Minkowski is wrongly designated as originator. The earlier works of Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
contain algebra and diagrams that correspond well with the Minkowski diagram. See for instance the plate of figures in Proceedings of the Royal Society in Edinburgh for 1900. Macfarlane was building on what one sees in William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
’s Elements of Dynamic (1878), page 90.
When abstracted to a line drawing, then any figure showing conjugate hyperbolas, with a selection of conjugate diameters, falls into this category. Students making drawings to accompany the exercises in George Salmon
George Salmon
The Reverend George Salmon was an Irish mathematician and theologian. His publications in algebraic geometry were widely read in the second half of the 19th century, but he devoted himself mostly to theology for the last forty years of his life...
’s A Treatise on Conic Sections (1900) at pages 165–71 (on conjugate diameters) will be making Minkowski diagrams.