Sylow theorem
Encyclopedia
In mathematics
, specifically in the field of finite group theory, the Sylow theorems are a collection of theorem
s named after the Norwegian
mathematician
Ludwig Sylow
(Sylow) that give detailed information about the number of subgroup
s of fixed order that a given finite group
contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups
.
For a prime number
p, a Sylow p-subgroup (sometimes p-Sylow subgroup) of a group G is a maximal p-subgroup of G, i.e., a subgroup of G which is a p-group
(so that the order of any group element is a power of p), and which is not a proper subgroup of any other p-subgroup of G. The set of all Sylow p-subgroups for a given prime p is sometimes written Sylp(G).
The Sylow theorems assert a partial converse to Lagrange's theorem
that for any finite group G the order (number of elements) of every subgroup of G divides the order of G. For any prime factor
p of the order of a finite group G, there exists a Sylow p-subgroup of G. The order of a Sylow p-subgroup of a finite group G is pn, where n is the multiplicity of p in the order of G, and any subgroup of order pn is a Sylow p-subgroup of G. The Sylow p-subgroups of a group (for fixed prime p) are conjugate
to each other. The number of Sylow p-subgroups of a group for fixed prime p is congruent to
to each other and have the largest possible order: if |G| = pnm with
where p does not divide m, then any Sylow p-subgroup P has order |P| = pn. That is, P is a p-group and gcd(|G:P|, p) = 1. These properties can be exploited to further analyze the structure of G.
The following theorems were first proposed and proven by Ludwig Sylow in 1872, and published in Mathematische Annalen
.
Theorem 1: For any prime factor
p with multiplicity n of the order of a finite group G, there exists a Sylow p-subgroup of G, of order pn.
The following weaker version of theorem 1 was first proved by Cauchy.
Corollary: Given a finite group G and a prime number p dividing the order of G, then there exists an element of order p in G .
Theorem 2: Given a finite group G and a prime number p, all Sylow p-subgroups of G are conjugate
to each other, i.e. if H and K are Sylow p-subgroups of G, then there exists an element g in G with g−1Hg = K.
Theorem 3: Let p be a prime factor with multiplicity n of the order of a finite group G, so that the order of G can be written as , where and p does not divide m. Let np be the number of Sylow p-subgroups of G. Then the following hold:
A very important consequence of Theorem 2 is that the condition np = 1 is equivalent to saying that the Sylow p-subgroup of G is a normal subgroup
(there are groups which have normal subgroups but no normal Sylow subgroups, such as S4).
.
Theorem: If K is a Sylow p-subgroup of G, and np = |Cl(K)| is finite, then every Sylow p-subgroup is conjugate to K, and np ≡ 1 mod p, where Cl(K) denotes the conjugacy class of K.
of the n-gon,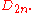
For n odd, 
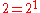is the highest power of 2 dividing the order, and thus subgroups of order 2 are Sylow subgroups. These are the groups generated by a reflection, of which there are n, and they are all conjugate under rotations; geometrically the axes of symmetry pass through a vertex and a side. By contrast, if n is even, then 4 divides the order of the group, and these are no longer Sylow subgroups, and in fact they fall into two conjugacy classes, geometrically according to whether they pass through two vertices or two faces. These are related by an outer automorphism, which can be represented by rotation through 
half the minimal rotation in the dihedral group.
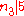and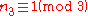 
. The only value satisfying these constraints is 1; therefore, there is only one subgroup of order 3, and it must be normal
(since it has no distinct conjugates). Similarly, n5 must divide 3, and n5 must equal 1 (mod 5); thus it must also have a single normal subgroup of order 5. Since 3 and 5 are coprime
, the intersection of these two subgroups is trivial, and so G must be the internal direct product of groups of order 3 and 5, that is the cyclic group
of order 15. Thus, there is only one group of order 15 (up to
isomorphism).
which is not cyclic
. Burnside's paqb theorem states that if the order of a group is the product of two prime power
s, then it is solvable
, and so the group is not simple, or is of prime order and is cyclic. This rules out every group up to order 30 (= 2 · 3 · 5).
If G is simple, and |G| = 30, then n3 must divide 10 ( = 2 · 5), and n3 must equal 1 (mod 3). Therefore n3 = 10, since neither 4 nor 7 divides 10, and if n3 = 1 then, as above, G would have a normal subgroup of order 3, and could not be simple. G then has 10 distinct cyclic subgroups of order 3, each of which has 2 elements of order 3 (plus the identity). This means G has at least 20 distinct elements of order 3. As well, n5 = 6, since n5 must divide 6 ( = 2 · 3), and n5 must equal 1 (mod 5). So G also has 24 distinct elements of order 5. But the order of G is only 30, so a simple group of order 30 cannot exist.
Next, suppose |G| = 42 = 2 · 3 · 7. Here n7 must divide 6 ( = 2 · 3) and n7 must equal 1 (mod 7), so n7 = 1. So, as before, G can not be simple.
On the other hand for |G| = 60 = 22 · 3 · 5, then n3 = 10 and n5 = 6 is perfectly possible. And in fact, the smallest simple non-cyclic group is A5, the alternating group over 5 elements. It has order 60, and has 24 cyclic permutation
s of order 5, and 20 of order 3.
shows that a Sylow subgroup of a normal subgroup provides a factorization of a finite group. A slight generalization known as Burnside's fusion theorem states that if G is a finite group with Sylow p-subgroup P and two subsets A and B normalized by P, then A and B are G-conjugate if and only if they are NG(P)-conjugate. The proof is a simple application of Sylow's theorem: If B=Ag, then the normalizer of B contains not only P but also Pg (since Pg is contained in the normalizer of Ag). By Sylow's theorem P and Pg are conjugate not only in G, but in the normalizer of B. Hence gh−1 normalizes P for some h that normalizes B, and then Agh−1 = Bh−1 = B, so that A and B are NG(P)-conjugate. Burnside's fusion theorem can be used to give a more power factorization called a semidirect product
: if G is a finite group whose Sylow p-subgroup P is contained in the center of its normalizer, then G has a normal subgroup K of order coprime to P, G = PK and P∩K = 1, that is, G is p-nilpotent.
Less trivial applications of the Sylow theorems include the focal subgroup theorem
, which studies the control a Sylow p-subgroup of the derived subgroup has on the structure of the entire group. This control is exploited at several stages of the classification of finite simple groups
, and for instance defines the case divisions used in the Alperin–Brauer–Gorenstein theorem classifying finite simple group
s whose Sylow 2-subgroup is a quasi-dihedral group. These rely on J. L. Alperin's strengthening of the conjugacy portion of Sylow's theorem to control what sorts of elements are used in the conjugation.
One proof of the Sylow theorems exploit the notion of group action
in various creative ways. The group G acts on itself or on the set of its p-subgroups in various ways, and each such action can be exploited to prove one of the Sylow theorems. The following proofs are based on combinatorial arguments of . In the following, we use a | b as notation for "a divides b" and a
b for the negation of this statement.
Proof: Let |G| = pkm = pk+ru such that p does not divide u, and let Ω denote the set of subsets of G of size pk. G acts
on Ω by left multiplication. The orbits
Gω = {gω | g ∈ G} of the ω ∈ Ω are the equivalence classes under the action of G.
For any ω ∈ Ω consider its stabilizer subgroup Gω.
For any fixed element α ∈ ω the function [g ↦ gα] maps Gω to ω injectively: for any two g,h ∈ Gω we have that gα = hα implies g = h, because α ∈ ω ⊆ G means that one may cancel on the right. Therefore pk = |ω| ≥ |Gω|.
On the other hand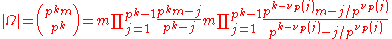
and no power of p remains in any of the factors inside the product on the right.
Hence νp(|Ω|) = νp(m) = r.
Let R ⊆ Ω be a complete representation of all the equivalence classes under the action of G. Then,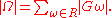
Thus, there exists an element ω ∈ R such that s := νp(|Gω|) ≤
νp(|Ω|) = r. Hence |Gω| = psv where p does not divide v.
By the stabilizer-orbit-theorem
we have
|Gω| = |G| / |Gω| = pk+r-su / v. Therefore
pk | |Gω|, so pk ≤ |Gω| and
Gω is the desired subgroup.
Proof: Write Ω as a disjoint sum of its orbits under G. Any element x ∈ Ω not fixed by G will lie in an orbit of order |G|/|Gx| (where Gx denotes the stabilizer), which is a multiple of p by assumption. The result follows immediately.
Proof: Let Ω be the set of left coset
s of P in G and let H act on Ω by left multiplication. Applying the Lemma to H on Ω, we see that |Ω0| ≡ |Ω| = [G : P] mod p. Now p
[G : P] by definition so p 
|Ω0|, hence in particular |Ω0| ≠ 0 so there exists some gP ∈ Ω0. It follows that for some g ∈ G and ∀ h ∈ H we have hgP = gP so g−1hgP ⊆ P and therefore g−1Hg ≤ P. Now if H is a Sylow p-subgroup, |H| = |P| = |gPg−1| so that H = gPg−1 for some g ∈ G.
Proof: By Theorem 2, np = [G : NG(P)], where P is any such subgroup, and NG(P) denotes the normalizer of P in G, so this number is a divisor of |G|/q. Let Ω be the set of all Sylow p-subgroups of G, and let P act on Ω by conjugation. Let Q ∈ Ω0 and observe that then Q = xQx−1 for all x ∈ P so that P ≤ NG(Q). By Theorem 2, P and Q are conjugate in NG(Q) in particular, and Q is normal in NG(Q), so then P = Q. It follows that Ω0 = {P} so that, by the Lemma, |Ω| ≡ |Ω0| = 1 mod p.
.
One proof of the existence of Sylow p-subgroups is constructive: if H is a p-subgroup of G and the index [G:H] is divisible by p, then the normalizer N = NG(H) of H in G is also such that [N:H] is divisible by p. In other words, a polycyclic generating system of a Sylow p-subgroup can be found by starting from any p-subgroup H (including the identity) and taking elements of p-power order contained in the normalizer of H but not in H itself. The algorithmic version of this (and many improvements) is described in textbook form in , including the algorithm described in . These versions are still used in the GAP computer algebra system
.
In permutation group
s, it has been proven in that a Sylow p-subgroup and its normalizer can be found in polynomial time of the input (the degree of the group times the number of generators). These algorithms are described in textbook form in , and are now becoming practical as the constructive recognition of finite simple groups becomes a reality. In particular, versions of this algorithm are used in the Magma computer algebra system
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the field of finite group theory, the Sylow theorems are a collection of theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s named after the Norwegian
Norway
Norway , officially the Kingdom of Norway, is a Nordic unitary constitutional monarchy whose territory comprises the western portion of the Scandinavian Peninsula, Jan Mayen, and the Arctic archipelago of Svalbard and Bouvet Island. Norway has a total area of and a population of about 4.9 million...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Ludwig Sylow
Peter Ludwig Mejdell Sylow
Peter Ludwig Mejdell Sylow was a Norwegianmathematician, who proved foundational results in group theory. He was born and died in Christiania ....
(Sylow) that give detailed information about the number of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of fixed order that a given finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
For a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, a Sylow p-subgroup (sometimes p-Sylow subgroup) of a group G is a maximal p-subgroup of G, i.e., a subgroup of G which is a p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
(so that the order of any group element is a power of p), and which is not a proper subgroup of any other p-subgroup of G. The set of all Sylow p-subgroups for a given prime p is sometimes written Sylp(G).
The Sylow theorems assert a partial converse to Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
that for any finite group G the order (number of elements) of every subgroup of G divides the order of G. For any prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
p of the order of a finite group G, there exists a Sylow p-subgroup of G. The order of a Sylow p-subgroup of a finite group G is pn, where n is the multiplicity of p in the order of G, and any subgroup of order pn is a Sylow p-subgroup of G. The Sylow p-subgroups of a group (for fixed prime p) are conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to each other. The number of Sylow p-subgroups of a group for fixed prime p is congruent to
Sylow theorems
Collections of subgroups which are each maximal in one sense or another are common in group theory. The surprising result here is that in the case of Sylp(G), all members are actually isomorphicGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to each other and have the largest possible order: if |G| = pnm with
where p does not divide m, then any Sylow p-subgroup P has order |P| = pn. That is, P is a p-group and gcd(|G:P|, p) = 1. These properties can be exploited to further analyze the structure of G.The following theorems were first proposed and proven by Ludwig Sylow in 1872, and published in Mathematische Annalen
Mathematische Annalen
Mathematische Annalen is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann...
.
Theorem 1: For any prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
p with multiplicity n of the order of a finite group G, there exists a Sylow p-subgroup of G, of order pn.
The following weaker version of theorem 1 was first proved by Cauchy.
Corollary: Given a finite group G and a prime number p dividing the order of G, then there exists an element of order p in G .
Theorem 2: Given a finite group G and a prime number p, all Sylow p-subgroups of G are conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to each other, i.e. if H and K are Sylow p-subgroups of G, then there exists an element g in G with g−1Hg = K.
Theorem 3: Let p be a prime factor with multiplicity n of the order of a finite group G, so that the order of G can be written as , where and p does not divide m. Let np be the number of Sylow p-subgroups of G. Then the following hold:
- np divides m, which is the indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
of the Sylow p-subgroup in G. - np ≡ 1 mod p.
- np = |G : NG(P)|, where P is any Sylow p-subgroup of G and NG denotes the normalizer.
Consequences
The Sylow theorems imply that for a prime number p every Sylow p-subgroup is of the same order, pn. Conversely, if a subgroup has order pn, then it is a Sylow p-subgroup, and so is isomorphic to every other Sylow p-subgroup. Due to the maximality condition, if H is any p-subgroup of G, then H is a subgroup of a p-subgroup of order pn.A very important consequence of Theorem 2 is that the condition np = 1 is equivalent to saying that the Sylow p-subgroup of G is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
(there are groups which have normal subgroups but no normal Sylow subgroups, such as S4).
Sylow theorems for infinite groups
There is an analogue of the Sylow theorems for infinite groups. We define a Sylow p-subgroup in an infinite group to be a p-subgroup (that is, every element in it has p-power order) which is maximal for inclusion among all p-subgroups in the group. Such subgroups exist by Zorn's lemmaZorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
.
Theorem: If K is a Sylow p-subgroup of G, and np = |Cl(K)| is finite, then every Sylow p-subgroup is conjugate to K, and np ≡ 1 mod p, where Cl(K) denotes the conjugacy class of K.
Examples
A simple illustration of Sylow subgroups and the Sylow theorems are the dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of the n-gon,
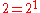For n odd, is the highest power of 2 dividing the order, and thus subgroups of order 2 are Sylow subgroups. These are the groups generated by a reflection, of which there are n, and they are all conjugate under rotations; geometrically the axes of symmetry pass through a vertex and a side. By contrast, if n is even, then 4 divides the order of the group, and these are no longer Sylow subgroups, and in fact they fall into two conjugacy classes, geometrically according to whether they pass through two vertices or two faces. These are related by an outer automorphism, which can be represented by rotation through half the minimal rotation in the dihedral group.Cyclic group orders
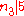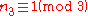Some numbers n are such that every group of order n is cyclic. One can show that n = 15 is such a number using the Sylow theorems: Let G be a group of order 15 = 3 · 5 and n3 be the number of Sylow 3-subgroups. Then and . The only value satisfying these constraints is 1; therefore, there is only one subgroup of order 3, and it must be normalNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
(since it has no distinct conjugates). Similarly, n5 must divide 3, and n5 must equal 1 (mod 5); thus it must also have a single normal subgroup of order 5. Since 3 and 5 are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, the intersection of these two subgroups is trivial, and so G must be the internal direct product of groups of order 3 and 5, that is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 15. Thus, there is only one group of order 15 (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism).
Small groups are not simple
A more complex example involves the order of the smallest simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
which is not cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. Burnside's paqb theorem states that if the order of a group is the product of two prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
s, then it is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
, and so the group is not simple, or is of prime order and is cyclic. This rules out every group up to order 30 (= 2 · 3 · 5).
If G is simple, and |G| = 30, then n3 must divide 10 ( = 2 · 5), and n3 must equal 1 (mod 3). Therefore n3 = 10, since neither 4 nor 7 divides 10, and if n3 = 1 then, as above, G would have a normal subgroup of order 3, and could not be simple. G then has 10 distinct cyclic subgroups of order 3, each of which has 2 elements of order 3 (plus the identity). This means G has at least 20 distinct elements of order 3. As well, n5 = 6, since n5 must divide 6 ( = 2 · 3), and n5 must equal 1 (mod 5). So G also has 24 distinct elements of order 5. But the order of G is only 30, so a simple group of order 30 cannot exist.
Next, suppose |G| = 42 = 2 · 3 · 7. Here n7 must divide 6 ( = 2 · 3) and n7 must equal 1 (mod 7), so n7 = 1. So, as before, G can not be simple.
On the other hand for |G| = 60 = 22 · 3 · 5, then n3 = 10 and n5 = 6 is perfectly possible. And in fact, the smallest simple non-cyclic group is A5, the alternating group over 5 elements. It has order 60, and has 24 cyclic permutation
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
s of order 5, and 20 of order 3.
Fusion results
Frattini's argumentFrattini's argument
In group theory, a branch of mathematics, Frattini's argument is an important lemma in the structure theory of finite groups. It is named after Giovanni Frattini, who first used it in a paper from 1885 when defining the Frattini subgroup of a group....
shows that a Sylow subgroup of a normal subgroup provides a factorization of a finite group. A slight generalization known as Burnside's fusion theorem states that if G is a finite group with Sylow p-subgroup P and two subsets A and B normalized by P, then A and B are G-conjugate if and only if they are NG(P)-conjugate. The proof is a simple application of Sylow's theorem: If B=Ag, then the normalizer of B contains not only P but also Pg (since Pg is contained in the normalizer of Ag). By Sylow's theorem P and Pg are conjugate not only in G, but in the normalizer of B. Hence gh−1 normalizes P for some h that normalizes B, and then Agh−1 = Bh−1 = B, so that A and B are NG(P)-conjugate. Burnside's fusion theorem can be used to give a more power factorization called a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
: if G is a finite group whose Sylow p-subgroup P is contained in the center of its normalizer, then G has a normal subgroup K of order coprime to P, G = PK and P∩K = 1, that is, G is p-nilpotent.
Less trivial applications of the Sylow theorems include the focal subgroup theorem
Focal subgroup theorem
In abstract algebra, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to . The focal subgroup theorem relates the ideas of transfer and...
, which studies the control a Sylow p-subgroup of the derived subgroup has on the structure of the entire group. This control is exploited at several stages of the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, and for instance defines the case divisions used in the Alperin–Brauer–Gorenstein theorem classifying finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s whose Sylow 2-subgroup is a quasi-dihedral group. These rely on J. L. Alperin's strengthening of the conjugacy portion of Sylow's theorem to control what sorts of elements are used in the conjugation.
Proof of the Sylow theorems
The Sylow theorems have been proved in a number of ways, and the history of the proofs themselves are the subject of many papers including , , , , and to some extent .One proof of the Sylow theorems exploit the notion of group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
in various creative ways. The group G acts on itself or on the set of its p-subgroups in various ways, and each such action can be exploited to prove one of the Sylow theorems. The following proofs are based on combinatorial arguments of . In the following, we use a | b as notation for "a divides b" and a
b for the negation of this statement.
Theorem 1: A finite group G whose order |G| is divisible by a prime power pk has a subgroup of order pk.
Proof: Let |G| = pkm = pk+ru such that p does not divide u, and let Ω denote the set of subsets of G of size pk. G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on Ω by left multiplication. The orbits
Gω = {gω | g ∈ G} of the ω ∈ Ω are the equivalence classes under the action of G.
For any ω ∈ Ω consider its stabilizer subgroup Gω.
For any fixed element α ∈ ω the function [g ↦ gα] maps Gω to ω injectively: for any two g,h ∈ Gω we have that gα = hα implies g = h, because α ∈ ω ⊆ G means that one may cancel on the right. Therefore pk = |ω| ≥ |Gω|.
On the other hand
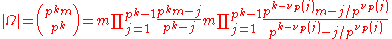
and no power of p remains in any of the factors inside the product on the right.
Hence νp(|Ω|) = νp(m) = r.
Let R ⊆ Ω be a complete representation of all the equivalence classes under the action of G. Then,
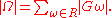
Thus, there exists an element ω ∈ R such that s := νp(|Gω|) ≤
νp(|Ω|) = r. Hence |Gω| = psv where p does not divide v.
By the stabilizer-orbit-theorem
we have
|Gω| = |G| / |Gω| = pk+r-su / v. Therefore
pk | |Gω|, so pk ≤ |Gω| and
Gω is the desired subgroup.
Lemma: Let G be a finite p-group, let G act on a finite set Ω, and let Ω0 denote the set of points of Ω that are fixed under the action of G. Then |Ω| ≡ |Ω0| mod p.
Proof: Write Ω as a disjoint sum of its orbits under G. Any element x ∈ Ω not fixed by G will lie in an orbit of order |G|/|Gx| (where Gx denotes the stabilizer), which is a multiple of p by assumption. The result follows immediately.
Theorem 2: If H is a p-subgroup of G and P is a Sylow p-subgroup of G, then there exists an element g in G such that g−1Hg ≤ P. In particular, all Sylow p-subgroups of G are conjugateConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to each other (and therefore isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
), i.e. if H and K are Sylow p-subgroups of G, then there exists an element g in G with g−1Hg = K.
Proof: Let Ω be the set of left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of P in G and let H act on Ω by left multiplication. Applying the Lemma to H on Ω, we see that |Ω0| ≡ |Ω| = [G : P] mod p. Now p
[G : P] by definition so p |Ω0|, hence in particular |Ω0| ≠ 0 so there exists some gP ∈ Ω0. It follows that for some g ∈ G and ∀ h ∈ H we have hgP = gP so g−1hgP ⊆ P and therefore g−1Hg ≤ P. Now if H is a Sylow p-subgroup, |H| = |P| = |gPg−1| so that H = gPg−1 for some g ∈ G.
Theorem 3: Let q denote the order of any Sylow p-subgroup of a finite group G. Then np | |G|/q and np ≡ 1 mod p.
Proof: By Theorem 2, np = [G : NG(P)], where P is any such subgroup, and NG(P) denotes the normalizer of P in G, so this number is a divisor of |G|/q. Let Ω be the set of all Sylow p-subgroups of G, and let P act on Ω by conjugation. Let Q ∈ Ω0 and observe that then Q = xQx−1 for all x ∈ P so that P ≤ NG(Q). By Theorem 2, P and Q are conjugate in NG(Q) in particular, and Q is normal in NG(Q), so then P = Q. It follows that Ω0 = {P} so that, by the Lemma, |Ω| ≡ |Ω0| = 1 mod p.
Algorithms
The problem of finding a Sylow subgroup of a given group is an important problem in computational group theoryComputational group theory
In mathematics, computational group theory is the study ofgroups by means of computers. It is concernedwith designing and analysing algorithms anddata structures to compute information about groups...
.
One proof of the existence of Sylow p-subgroups is constructive: if H is a p-subgroup of G and the index [G:H] is divisible by p, then the normalizer N = NG(H) of H in G is also such that [N:H] is divisible by p. In other words, a polycyclic generating system of a Sylow p-subgroup can be found by starting from any p-subgroup H (including the identity) and taking elements of p-power order contained in the normalizer of H but not in H itself. The algorithmic version of this (and many improvements) is described in textbook form in , including the algorithm described in . These versions are still used in the GAP computer algebra system
GAP computer algebra system
GAP is a computer algebra system for computational discrete algebra with particular emphasis on computational group theory.-History:...
.
In permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s, it has been proven in that a Sylow p-subgroup and its normalizer can be found in polynomial time of the input (the degree of the group times the number of generators). These algorithms are described in textbook form in , and are now becoming practical as the constructive recognition of finite simple groups becomes a reality. In particular, versions of this algorithm are used in the Magma computer algebra system
Magma computer algebra system
Magma is a computer algebra system designed to solve problems in algebra, number theory, geometry and combinatorics. It is named after the algebraic structure magma...
.