Dihedral group of order 6
Encyclopedia
The smallest non-abelian group has 6 elements. It is a dihedral group
with notation D3 (or D6, both are used) and the symmetric group
of degree 3, with notation S3.
This page illustrates many group concepts using this group as example.
of an equilateral triangle. In contrast with the case of a square
or other polygon, all permutations of the vertices can be achieved by rotation and flipping over (or reflecting).
In 3D there are two different symmetry groups which are algebraically the group D3:
In multiplicative form, we traditionally write xy for the combined action "first do y, then do x"; so that ab is the action RGB → RBG → BRG, i.e., "take the last block and move it to the front".
If we write e for "leave the blocks as they are" (the identity action), then we can write the six permutation
s of the set of three blocks as the following actions:
Note that the action aa has the effect RGB → GRB → RGB, leaving the blocks as they were; so we can write aa = e.
Similarly,
so each of the above actions has an inverse.
By inspection, we can also determine associativity and closure; note for example that
The group is non-abelian since, for example, ab ≠ ba. Since it is built up from the basic actions a and b, we say that the set {a,b} generates
it.
The group has presentation
where a and b are swaps and r is a cyclic permutation.
In the form of a Cayley table
:
Note that non-equal non-identity elements only commute if they are each other's inverse. Therefore the group is centerless.
es of the group:
For example (RG) and (RB) are both of the form (x y); a permutation of the letters R, G, and B (namely (GB)) changes the notation (RG) into (RB). Therefore, if we apply (GB), then (RB), and then the inverse of (GB), which is also (GB), the resulting permutation is (RG).
Note that conjugate group elements always have the same order, but for groups in general group elements that have the same order need not be conjugate.
we know that any non-trivial subgroup
has order 2 or 3. In fact the two cyclic permutations of all three blocks, with the identity, form a subgroup of order 3, index
2, and the swaps of two blocks, each with the identity, form three subgroups of order 2, index 3.
The first-mentioned is {,(RGB),(RBG)}, the alternating group A3.
The left coset
s and the right cosets of A3 are both that subgroup itself and the three swaps.
The left cosets of {,(RG)} are:
The right cosets of {(RG),} are:
Thus A3 is normal
, and the other three non-trivial subgroups are not. The quotient group
G / A3 is isomorphic with C2.
, a semidirect product
, where H is a subgroup of two elements: and one of the three swaps.
In terms of permutations the two group elements of G/ A3 are the set of even permutations
and the set of odd permutations.
If the original group is that generated by a 120° rotation of a plane about a point, and reflection with respect to a line through that point, then the quotient group has the two elements which can be described as the subsets "just rotate (or do nothing)" and "take a mirror image
".
Note that for the symmetry group of a square, an uneven permutation of vertices does not correspond to taking a mirror image, but to operations not allowed for rectangles, i.e. 90° rotation and applying a diagonal axis of reflection.
is 
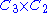if both φ(0) and φ(1) are the identity.
The semidirect product is isomorphic to the dihedral group of order 6 if φ(0) is the identity and φ(1) is the non-trivial automorphism of C3, which inverses the elements.
Thus we get: * (n2, h2) = (n1 + n2, h2) * (n2, h2) = (n1 - n2, 1 + h2)
for all n1, n2 in C3 and h2 in C2.
In a Cayley table:
00 10 20 01 11 21
00 00 10 20 01 11 21
10 10 20 00 11 21 01
20 20 00 10 21 01 11
01 01 21 11 00 20 10
11 11 01 21 10 00 20
21 21 11 01 20 10 00
Note that for the second digit we essentially have a 2x2 table, with 3x3 equal values for each of these 4 cells. For the first digit the left half of the table is the same as the right half, but the top half is different from the bottom half.
For the direct product the table is the same except that the first digits of the bottom half of the table are the same as in the top half.
of isometries of the plane, and consider the corresponding group action
on a set of 30 evenly spaced points on a circle, numbered 0 to 29, with 0 at one of the reflexion axes.
This section illustrates group action concepts for this case.
The action of G on X is called
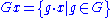
The orbits are {0,10,20}, {1,9,11,19,21,29}, {2,8,12,18,22,28}, {3,7,13,17,23,27}, {4,6,14,16,24,26}, and {5,15,25}. The points within an orbit are "equivalent". If a symmetry group applies for a pattern, then within each orbit the color is the same.
The set of all orbits of X under the action of G is written as X / G.
If Y is a subset
of X, we write GY for the set { g · y : y
Y and g 
G }. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = y for all g in G and all y in Y. The union of e.g. two orbits is invariant under G, but not fixed.
For every x in X, we define the stabilizer subgroup of x (also called the isotropy group or little group) as the set of all elements in G that fix x: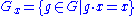
If x is a reflection point (0, 5, 10, 15, 20, or 25), its stabilizer is the group of order two containing the identity and the reflection in x. In other cases the stabilizer is the trivial group.
For a fixed x in X, consider the map from G to X given by g |-> g · x. The image
of this map is the orbit of x and the coimage
is the set of all left coset
s of Gx. The standard quotient theorem of set theory then gives a natural bijection
between G/Gx and Gx. Specifically, the bijection is given by hGx |-> h · x. This result is known as the orbit-stabilizer theorem. In the two cases of a small orbit, the stabilizer is non-trivial.
If two elements x and y belong to the same orbit, then their stabilizer subgroups, Gx and Gy, are isomorphic
. More precisely: if y = g · x, then Gy = gGx g−1. In the example this applies e.g. for 5 and 25, both reflection points. Reflection about 25 corresponds to a rotation of -20, reflection about 3, and rotation of 20.
A result closely related to the orbit-stabilizer theorem is Burnside's lemma
:
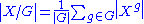
where Xg is the set of points fixed by g. I.e., the number of orbits is equal to the average number of points fixed per group element.
For the identity all 30 points are fixed, for the two rotations none, and for the three reflections two each: {0,15}, {5,20}, and {10, 25}. Thus the average is six, the number of orbits.
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
with notation D3 (or D6, both are used) and the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of degree 3, with notation S3.
This page illustrates many group concepts using this group as example.
Symmetry groups
In 2D the group D3 is the symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of an equilateral triangle. In contrast with the case of a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
or other polygon, all permutations of the vertices can be achieved by rotation and flipping over (or reflecting).
In 3D there are two different symmetry groups which are algebraically the group D3:
- one with a 3-fold rotation axis and a perpendicular 2-fold rotation axis (hence three of these): D3
- one with a 3-fold rotation axis in a plane of reflection (and hence also in two other planes of reflection): C3v
Permutations of a set of three objects
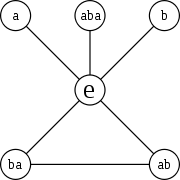
Consider three colored blocks (red, green, and blue), initially placed in the order RGB. Let a be the action "swap the first block and the second block", and let b be the action "swap the second block and the third block".If we write e for "leave the blocks as they are" (the identity action), then we can write the six permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the set of three blocks as the following actions:
- e : RGB → RGB or
- a : RGB → GRB or (RG)
- b : RGB → RBG or (GB)
- ab : RGB → BRG or (RBG)
- ba : RGB → GBR or (RGB)
- aba : RGB → BGR or (RB)
Note that the action aa has the effect RGB → GRB → RGB, leaving the blocks as they were; so we can write aa = e.
Similarly,
- bb = e,
- (aba)(aba) = e, and
- (ab)(ba) = (ba)(ab) = e;
so each of the above actions has an inverse.
By inspection, we can also determine associativity and closure; note for example that
- (ab)a = a(ba) = aba, and
- (ba)b = b(ab) = aba.
The group is non-abelian since, for example, ab ≠ ba. Since it is built up from the basic actions a and b, we say that the set {a,b} generates
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
it.
The group has presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
-
, also written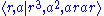 
- or
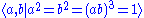, also written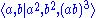 
where a and b are swaps and r is a cyclic permutation.
Summary of group operations
With x, y, and z different blocks R, G, and B we have:- (xyz)(xyz)=(xzy)
- (xyz)(xzy)=
- (xyz)(xy)=(xz)
- (xy)(xyz)=(yz)
- (xy)(xy)=
- (xy)(xz)=(xzy)
In the form of a Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
:
| * | e | a | b | c | d | f |
|---|---|---|---|---|---|---|
| e | e | a | b | c | d | f |
| a | a | e | d | f | b | c |
| b | b | f | e | d | c | a |
| c | c | d | f | e | a | b |
| d | d | c | a | b | f | e |
| f | f | b | c | a | e | d |
Note that non-equal non-identity elements only commute if they are each other's inverse. Therefore the group is centerless.
Conjugacy classes
We can easily distinguish three kinds of permutations of the three blocks, called conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of the group:
- no change , a group element of orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
1 - interchanging two blocks: (RG), (RB), (GB), three group elements of order 2
- a cyclic permutation of all three blocks (RGB), (RBG), two group elements of order 3
For example (RG) and (RB) are both of the form (x y); a permutation of the letters R, G, and B (namely (GB)) changes the notation (RG) into (RB). Therefore, if we apply (GB), then (RB), and then the inverse of (GB), which is also (GB), the resulting permutation is (RG).
Note that conjugate group elements always have the same order, but for groups in general group elements that have the same order need not be conjugate.
Subgroups
From Lagrange's theoremLagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
we know that any non-trivial subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
has order 2 or 3. In fact the two cyclic permutations of all three blocks, with the identity, form a subgroup of order 3, index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2, and the swaps of two blocks, each with the identity, form three subgroups of order 2, index 3.
The first-mentioned is {,(RGB),(RBG)}, the alternating group A3.
The left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s and the right cosets of A3 are both that subgroup itself and the three swaps.
The left cosets of {,(RG)} are:
- that subgroup itself
- {(RB),(RGB)}
- {(GB),(RBG)}
The right cosets of {(RG),} are:
- that subgroup itself
- {(RBG),(RB)}
- {(RGB),(GB)}
Thus A3 is normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, and the other three non-trivial subgroups are not. The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G / A3 is isomorphic with C2.
, a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
, where H is a subgroup of two elements: and one of the three swaps.
In terms of permutations the two group elements of G/ A3 are the set of even permutations
Even and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
and the set of odd permutations.
If the original group is that generated by a 120° rotation of a plane about a point, and reflection with respect to a line through that point, then the quotient group has the two elements which can be described as the subsets "just rotate (or do nothing)" and "take a mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
".
Note that for the symmetry group of a square, an uneven permutation of vertices does not correspond to taking a mirror image, but to operations not allowed for rectangles, i.e. 90° rotation and applying a diagonal axis of reflection.
Semidirect products
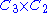is if both φ(0) and φ(1) are the identity.The semidirect product is isomorphic to the dihedral group of order 6 if φ(0) is the identity and φ(1) is the non-trivial automorphism of C3, which inverses the elements.
Thus we get: * (n2, h2) = (n1 + n2, h2) * (n2, h2) = (n1 - n2, 1 + h2)
for all n1, n2 in C3 and h2 in C2.
In a Cayley table:
00 10 20 01 11 21
00 00 10 20 01 11 21
10 10 20 00 11 21 01
20 20 00 10 21 01 11
01 01 21 11 00 20 10
11 11 01 21 10 00 20
21 21 11 01 20 10 00
Note that for the second digit we essentially have a 2x2 table, with 3x3 equal values for each of these 4 cells. For the first digit the left half of the table is the same as the right half, but the top half is different from the bottom half.
For the direct product the table is the same except that the first digits of the bottom half of the table are the same as in the top half.
Group action
Consider D3 in the geometrical way, as symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of isometries of the plane, and consider the corresponding group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set of 30 evenly spaced points on a circle, numbered 0 to 29, with 0 at one of the reflexion axes.
This section illustrates group action concepts for this case.
The action of G on X is called
- transitive if for any two x, y in X there exists an g in G such that g·x = y; - this is not the case
- faithful (or effective) if for any two different g, h in G there exists an x in X such that g·x ≠ h·x; - this is the case, because, except for the identity, symmetry groups do not contain elements that "do nothing"
- free if for any two different g, h in G and all x in X we have g·x ≠ h·x; - this is not the case because there are reflections
Orbits and stabilizers
The orbit of a point x in X is the set of elements of X to which x can be moved by the elements of G. The orbit of x is denoted by Gx: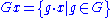The orbits are {0,10,20}, {1,9,11,19,21,29}, {2,8,12,18,22,28}, {3,7,13,17,23,27}, {4,6,14,16,24,26}, and {5,15,25}. The points within an orbit are "equivalent". If a symmetry group applies for a pattern, then within each orbit the color is the same.
The set of all orbits of X under the action of G is written as X / G.
If Y is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X, we write GY for the set { g · y : y
Y and g G }. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = y for all g in G and all y in Y. The union of e.g. two orbits is invariant under G, but not fixed.For every x in X, we define the stabilizer subgroup of x (also called the isotropy group or little group) as the set of all elements in G that fix x:
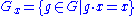
If x is a reflection point (0, 5, 10, 15, 20, or 25), its stabilizer is the group of order two containing the identity and the reflection in x. In other cases the stabilizer is the trivial group.
For a fixed x in X, consider the map from G to X given by g |-> g · x. The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of this map is the orbit of x and the coimage
Coimage
In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies....
is the set of all left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of Gx. The standard quotient theorem of set theory then gives a natural bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between G/Gx and Gx. Specifically, the bijection is given by hGx |-> h · x. This result is known as the orbit-stabilizer theorem. In the two cases of a small orbit, the stabilizer is non-trivial.
If two elements x and y belong to the same orbit, then their stabilizer subgroups, Gx and Gy, are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. More precisely: if y = g · x, then Gy = gGx g−1. In the example this applies e.g. for 5 and 25, both reflection points. Reflection about 25 corresponds to a rotation of -20, reflection about 3, and rotation of 20.
A result closely related to the orbit-stabilizer theorem is Burnside's lemma
Burnside's lemma
Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy-Frobenius lemma or the orbit-counting theorem, is a result in group theory which is often useful in taking account of symmetry when counting mathematical objects. Its various eponyms include William Burnside, George...
:
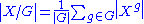
where Xg is the set of points fixed by g. I.e., the number of orbits is equal to the average number of points fixed per group element.
For the identity all 30 points are fixed, for the two rotations none, and for the three reflections two each: {0,15}, {5,20}, and {10, 25}. Thus the average is six, the number of orbits.