Quasidihedral group
Encyclopedia
In mathematics
, the quasi-dihedral groups and semi-dihedral groups are non-abelian group
s of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of nonabelian groups of order 2n which have a cyclic subgroup of index
2. Two are well established, the generalized quaternion group and the dihedral group
, but the other two have conflicting names, so this article discusses both groups.
One of the groups is often considered particularly important, since it is an example of a 2-group of maximal nilpotency class. In Bertram Huppert
's influential text Endliche Gruppen, this group is called a Quasidiedergruppe. In Daniel Gorenstein
's influential text, Finite Groups, this group is called the semidihedral group. In this article, we call this group the quasidihedral group. Both books give the same presentation for this group:
.
The other non-abelian 2-group with cyclic subgroup of index 2 is not given a special name in either text, but referred to as just G or M_m(2). In this article, this group is called the other-maximal-cyclic group. Its presentation in both texts is:
.
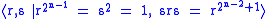Both these two groups and the dihedral group are semidirect product
s of a cyclic group <r> of order 2n-1 with a cyclic group <s> of order 2. Such a non-abelian semi-direct product is uniquely determined by an element of order 2 in the group of units of the ring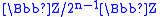
and there are precisely three such elements, 
, 
, and 
, corresponding to the dihedral group, the quasidihedral, and the other-maximal-cyclic group.
The generalized quaternion group, the dihedral group, and the quasidihedral group of order 2n all have nilpotency class n−1, and are the only isomorphism classes of groups of order 2n with nilpotency class n−1. The groups of order pn and nilpotency class n−1 were the beginning of the classification of all p-group
s via coclass. The other-maximal-cyclic group of order 2n always has nilpotency class 2. This makes the other-maximal-cyclic group less interesting, since most groups of order pn for large n have nilpotency class 2 and have proven difficult to understand directly.
The generalized quaternion, the dihedral, and the quasidihedral group are the only 2-groups whose derived subgroup has index 4. The Alperin–Brauer–Gorenstein theorem classifies the simple groups, and to a degree the finite groups, with quasidihedral Sylow 2-subgroups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the quasi-dihedral groups and semi-dihedral groups are non-abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of nonabelian groups of order 2n which have a cyclic subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2. Two are well established, the generalized quaternion group and the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, but the other two have conflicting names, so this article discusses both groups.
One of the groups is often considered particularly important, since it is an example of a 2-group of maximal nilpotency class. In Bertram Huppert
Bertram Huppert
Bertram Huppert is a German mathematician specializing in group theory and the representation theory of finite groups. His Endliche Gruppen is an influential textbook in group theory, and he has over 50 doctoral descendants.-Education:Bertram Huppert went to school in Bonn from 1934 until 1945...
's influential text Endliche Gruppen, this group is called a Quasidiedergruppe. In Daniel Gorenstein
Daniel Gorenstein
Daniel E. Gorenstein was an American mathematician. He earned his undergraduate and graduate degrees at Harvard University, where he earned his Ph.D. in 1950 under Oscar Zariski, introducing in his dissertation Gorenstein rings...
's influential text, Finite Groups, this group is called the semidihedral group. In this article, we call this group the quasidihedral group. Both books give the same presentation for this group:
.The other non-abelian 2-group with cyclic subgroup of index 2 is not given a special name in either text, but referred to as just G or M_m(2). In this article, this group is called the other-maximal-cyclic group. Its presentation in both texts is:
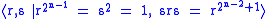.Both these two groups and the dihedral group are semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
s of a cyclic group <r> of order 2n-1 with a cyclic group <s> of order 2. Such a non-abelian semi-direct product is uniquely determined by an element of order 2 in the group of units of the ring
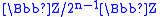and there are precisely three such elements, , , and 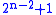, corresponding to the dihedral group, the quasidihedral, and the other-maximal-cyclic group.The generalized quaternion group, the dihedral group, and the quasidihedral group of order 2n all have nilpotency class n−1, and are the only isomorphism classes of groups of order 2n with nilpotency class n−1. The groups of order pn and nilpotency class n−1 were the beginning of the classification of all p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s via coclass. The other-maximal-cyclic group of order 2n always has nilpotency class 2. This makes the other-maximal-cyclic group less interesting, since most groups of order pn for large n have nilpotency class 2 and have proven difficult to understand directly.
The generalized quaternion, the dihedral, and the quasidihedral group are the only 2-groups whose derived subgroup has index 4. The Alperin–Brauer–Gorenstein theorem classifies the simple groups, and to a degree the finite groups, with quasidihedral Sylow 2-subgroups.