Inner automorphism
Encyclopedia
In abstract algebra
an inner automorphism is a function
which, informally, involves a certain operation being applied, then another one (x) performed, and then the initial operation being reversed. Sometimes this has a net effect ("take off shoes, take off socks, put on shoes"), and sometimes it does not ("take off left glove, take off right glove, put on left glove" or "take off right glove" are equivalent).
More formally an inner automorphism of a group
G is a function:
defined by
where a is a given fixed element of G.
The operation a−1xa is called conjugation (see also conjugacy class
).
In fact
is equivalent to saying
Therefore the existence and number of inner automorphisms that are not the identity mapping is a kind of measure of the failure of the commutative law in the group.
of G on itself).
; meaning (xy)a = xaya.
Inn(G) is a normal subgroup
of the full automorphism group Aut(G) of G. The quotient group
is known as the outer automorphism group
Out(G). The outer automorphism group measures, in a sense, how many automorphisms of G are not inner. Every non-inner automorphism yields a non-trivial element of Out(G), but different non-inner automorphisms may yield the same element of Out(G).
By associating the element a in G with the inner automorphism ƒ(x) = xa in Inn(G) as above, one obtains an isomorphism
between the quotient group
G/Z(G) (where Z(G) is the center of G) and the inner automorphism group:
This is a consequence of the first isomorphism theorem
, because Z(G) is precisely the set of those elements of G that give the identity mapping as corresponding inner automorphism (conjugation changes nothing).
It is an open problem whether every non-abelian p-group G has an automorphism of order p.
The latter question has positive answer whenever G has one of the following conditions:
) if and only if
G is abelian
.
Inn(G) can only be a cyclic group
when it is trivial, by a basic result on the center of a group.
At the opposite end of the spectrum, it is possible that the inner automorphisms exhaust the entire automorphism group; a group whose automorphisms are all inner is called complete
.
If the inner automorphism group of a perfect group
G is simple, then G is called quasisimple
.
R and a unit
u in R, the map ƒ(x) = u−1xu is a ring automorphism
of R. The ring automorphisms of this form are called inner automorphisms of R. They form a normal subgroup of the automorphism group of R.
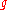is called an inner automorphism if it is of the form Adg, where Ad is the adjoint map and g is an element of a Lie group
whose Lie algebra is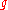
. The notion of inner automorphism for Lie algebras is compatible with the notion for groups in the sense that an inner automorphism of a Lie group induces a unique inner automorphism of the corresponding Lie algebra.
A, then an inner automorphism on G can be extended to a projectivity on the projective space
over A by inversive ring geometry
. In particular, the inner automorphisms of the classical linear groups
can be so extended.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
an inner automorphism is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which, informally, involves a certain operation being applied, then another one (x) performed, and then the initial operation being reversed. Sometimes this has a net effect ("take off shoes, take off socks, put on shoes"), and sometimes it does not ("take off left glove, take off right glove, put on left glove" or "take off right glove" are equivalent).
More formally an inner automorphism of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a function:
- ƒ: G → G
defined by
- ƒ(x) = a−1xa, for all x in G,
where a is a given fixed element of G.
The operation a−1xa is called conjugation (see also conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
).
In fact
- a−1xa = x
is equivalent to saying
- ax = xa.
Therefore the existence and number of inner automorphisms that are not the identity mapping is a kind of measure of the failure of the commutative law in the group.
Notation
The expression a−1xa is often denoted exponentially by xa. This notation is used because we have the rule (xa)b=xab (giving a right actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on itself).
Properties
Every inner automorphism is indeed an automorphism of the group G, i.e. it is a bijective map from G to G and it is a homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
; meaning (xy)a = xaya.
Inner and outer automorphism groups
The composition of two inner automorphisms is again an inner automorphism (as mentioned above: (xa)b=xab, and with this operation, the collection of all inner automorphisms of G is itself a group, the inner automorphism group of G denoted Inn(G).Inn(G) is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the full automorphism group Aut(G) of G. The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
- Aut(G)/Inn(G)
is known as the outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
Out(G). The outer automorphism group measures, in a sense, how many automorphisms of G are not inner. Every non-inner automorphism yields a non-trivial element of Out(G), but different non-inner automorphisms may yield the same element of Out(G).
By associating the element a in G with the inner automorphism ƒ(x) = xa in Inn(G) as above, one obtains an isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
between the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G/Z(G) (where Z(G) is the center of G) and the inner automorphism group:
- G/Z(G) = Inn(G).
This is a consequence of the first isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
, because Z(G) is precisely the set of those elements of G that give the identity mapping as corresponding inner automorphism (conjugation changes nothing).
Non-inner automorphisms of finite p-groups
A result of Wolfgang Gaschütz says that if G is a finite non-abelian p-group, then G has an automorphism of p-power order which is not inner.It is an open problem whether every non-abelian p-group G has an automorphism of order p.
The latter question has positive answer whenever G has one of the following conditions:
- G is nilpotent of class 2
- G is a regular p-groupRegular p-groupIn mathematical finite group theory, the concept of regular p-group captures some of the more important properties of abelian p-groups, but is general enough to include most "small" p-groups...
- The centralizer CG(Z(
(G))) in G of the center of the Frattini subgroupFrattini subgroupIn mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
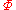(G) of G is not equal to 
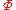(G) - G/Z(G) is a powerful p-groupPowerful p-groupIn mathematics, in the field of group theory, especially in the study of p-groups and pro-p-groups, the concept of powerful p-groups plays an important role. They were introduced in , where a number of applications are given, including results on Schur multipliers...
Types of groups
It follows that the group Inn(G) of inner automorphisms is itself trivial (i.e. consists only of the identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
G is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
.
Inn(G) can only be a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
when it is trivial, by a basic result on the center of a group.
At the opposite end of the spectrum, it is possible that the inner automorphisms exhaust the entire automorphism group; a group whose automorphisms are all inner is called complete
Complete group
In mathematics, a group G is said to be complete if every automorphism of G is inner, and the group is a centerless group; that is, it has a trivial outer automorphism group and trivial center....
.
If the inner automorphism group of a perfect group
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
G is simple, then G is called quasisimple
Quasisimple group
In mathematics, a quasisimple group is a group that is a perfect central extension E of a simple group S...
.
Ring case
Given a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R and a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
u in R, the map ƒ(x) = u−1xu is a ring automorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
of R. The ring automorphisms of this form are called inner automorphisms of R. They form a normal subgroup of the automorphism group of R.
Lie algebra case
An automorphism of a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
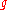is called an inner automorphism if it is of the form Adg, where Ad is the adjoint map and g is an element of a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
whose Lie algebra is
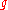. The notion of inner automorphism for Lie algebras is compatible with the notion for groups in the sense that an inner automorphism of a Lie group induces a unique inner automorphism of the corresponding Lie algebra.Extension
If G arises as the group of units of a ringRing theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
A, then an inner automorphism on G can be extended to a projectivity on the projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
over A by inversive ring geometry
Inversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
. In particular, the inner automorphisms of the classical linear groups
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
can be so extended.