Euclidean plane isometry - AbsoluteAstronomy.com

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a Euclidean plane isometry is an isometry

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length. There are four types: translations, rotations, reflections

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

, and glide reflection

Glide reflection

In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...

s (see below under classification of Euclidean plane isometries).

The set of Euclidean plane isometries forms a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

under composition

Function composition

In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...

: the Euclidean group

Euclidean group

In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...

in two dimensions. It is generated by reflections in lines, and every element of the Euclidean group is the composite of at most three distinct reflections.

Informal discussion

Informally, a Euclidean plane isometry is any way of transforming the plane without "deforming" it. For example, suppose that the Euclidean plane is represented by a sheet of transparent plastic sitting on a desk. Examples of isometries include:

Shifting the sheet one inch to the right.
Rotating the sheet by ten degrees around some marked point (which remains motionless).
Turning the sheet upside down. Notice that if a picture is drawn on one side of the sheet, then after turning the sheet upside down, we see the mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...

of the picture.

These are examples of translations, rotations, and reflection

Reflection (mathematics)

s respectively. There is one further type of isometry, called a glide reflection

Glide reflection

(see below under classification of Euclidean plane isometries).

However, folding, cutting, or melting the sheet are not considered isometries. Neither are less drastic alterations like bending, stretching, or twisting.

Formal definition

An isometry of the Euclidean plane is a distance-preserving transformation of the plane. That is, it is a map

Map (mathematics)

In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...

such that for any points p and q in the plane,

where d(p, q) is the usual Euclidean distance

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

between p and q.

Classification of Euclidean plane isometries

It can be shown that there are four types of Euclidean plane isometries (five if we include the identity). (Note: the notations for the types of isometries listed below are not completely standardised.)

Translations, denoted by T_v, where v is a vector in R². This has the effect of shifting the plane in the direction of v. That is, for any point p in the plane,

or in terms of (x, y) coordinates,

Rotations
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...

, denoted by R_c,θ, where c is a point in the plane (the centre of rotation), and θ is the angle of rotation. In terms of coordinates, rotations are most easily expressed by breaking them up into two operations. First, a rotation around the origin is given by

These matrices are the orthogonal matrices

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

(i.e. each is a square matrix G whose transpose

Transpose

In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

is its inverse, i.e.

), with determinant 1 (the other possibility for orthogonal matrices is −1, which gives a mirror image, see below). They form the special orthogonal group

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

SO(2).

A rotation around c can be accomplished by first translating c to the origin, then performing the rotation around the origin, and finally translating the origin back to c. That is,

or in other words,

Alternatively, a rotation around the origin is performed, followed by a translation:

Reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

s, or mirror isometries, denoted by F_c,v, where c is a point in the plane and v is a unit vector in R². (F is for "flip".) This has the effect of reflecting the point p in the line L that is perpendicular to v and that passes through c. The line L is called the reflection axis or the associated mirror. To find a formula for F_c,v, we first use the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

to find the component t of p − c in the v direction,

and then we obtain the reflection of p by subtraction,

The combination of rotations about the origin and reflections about a line through the origin is obtained with all orthogonal matrices (i.e. with determinant 1 and -1) forming orthogonal group O(2). In the case of a determinant of -1 we have:

which is a reflection in the x-axis followed by a rotation by an angle θ, or equivalently, a reflection in a line making an angle of θ/2 with the x-axis. Reflection in a parallel line corresponds to adding a vector perpendicular to it.

Glide reflection
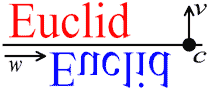Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...

s, denoted by G_c,v,w, where c is a point in the plane, v is a unit vector in R², and w is a vector perpendicular to v. This is a combination of a reflection in the line described by c and v, followed by a translation along w. That is,

or in other words,

= F_{c,v}(p + w);\,

that is, we obtain the same result if we do the translation and the reflection in the opposite order.)

Alternatively we multiply by an orthogonal matrix with determinant -1 (corresponding to a reflection in a line through the origin), followed by a translation. This is a glide reflection, except in the special case that the translation is perpendicular to the line of reflection, in which case the combination is itself just a reflection in a parallel line.

The identity

Identity (mathematics)

In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...

isometry, defined by I(p) = p for all points p, can be considered a fifth kind. Thus there are five mutually exclusive categories. Alternatively, we can consider the identity a special case of a translation, and also a special case of a rotation. Similarly we can consider every reflection to be a special case of a glide reflection. In that case we have only three categories: rotations, translations, and glide reflections, which are mutually exclusive except for the identity.

In all cases we multiply the position vector by an orthogonal matrix and add a vector; if the determinant is 1 we have a rotation, a translation, or the identity, and if it is −1 we have a glide reflection or a reflection.

A "random" isometry, like taking a sheet of paper from a table and randomly laying it back, "almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

" is a rotation or a glide reflection (they have three degrees of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

). This applies regardless of the details of the probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

, as long as θ and the direction of the added vector are independent

Statistical independence

In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...

and uniformly distributed

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

and the length of the added vector has a continuous distribution. A pure translation and a pure reflection are special cases with only two degrees of freedom, while the identity is even more special, with no degrees of freedom.

Isometries as reflection group

Reflections, or mirror isometries, can be combined to produce any isometry. Thus isometries are an example of a reflection group

Reflection group

In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...

Mirror combinations

In the Euclidean plane, we have the following possibilities.

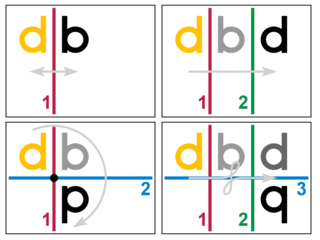
[d ] Identity

Two reflections in the same mirror restore each point to its original position. All points are left fixed. Any pair of identical mirrors has the same effect.

[db] Reflection

As Alice found through the looking-glass

Through the Looking-Glass

Through the Looking-Glass, and What Alice Found There is a work of literature by Lewis Carroll . It is the sequel to Alice's Adventures in Wonderland...

, a single mirror causes left and right hands to switch. (In formal terms, topological orientation is reversed.) Points on the mirror are left fixed. Each mirror has a unique effect.

[dp] Rotation

Two distinct intersecting mirrors have a single point in common, which remains fixed. All other points rotate around it by twice the angle between the mirrors. Any two mirrors with the same fixed point and same angle give the same rotation, so long as they are used in the correct order.

[dd] Translation

Two distinct mirrors that do not intersect must be parallel. Every point moves the same amount, twice the distance between the mirrors, and in the same direction. No points are left fixed. Any two mirrors with the same parallel direction and the same distance apart give the same translation, so long as they are used in the correct order.

[dq] Glide reflection

Three mirrors. If they are all parallel, the effect is the same as a single mirror (slide a pair to cancel the third). Otherwise we can find an equivalent arrangement where two are parallel and the third is perpendicular to them. The effect is a reflection combined with a translation parallel to the mirror. No points are left fixed.

Three mirrors suffice

Adding more mirrors does not add more possibilities (in the plane), because they can always be rearranged to cause cancellation.

Proof. An isometry is completely determined by its effect on three independent (not collinear) points. So suppose p₁, p₂, p₃ map to q₁, q₂, q₃; we can generate a sequence of mirrors to achieve this as follows. If p₁ and q₁ are distinct, choose their perpendicular bisector as mirror. Now p₁ maps to q₁; and we will pass all further mirrors through q₁, leaving it fixed. Call the images of p₂ and p₃ under this reflection p₂′ and p₃′. If q₂ is distinct from p₂′, bisect the angle at q₁ with a new mirror. With p₁ and p₂ now in place, p₃ is at p₃′′; and if it is not in place, a final mirror through q₁ and q₂ will flip it to q₃. Thus at most three reflections suffice to reproduce any plane isometry. ∎

Recognition

We can recognize which of these isometries we have according to whether it preserves hands or swaps them, and whether it has at least one fixed point or not, as shown in the following table (omitting the identity).

		Preserves hands?
		Yes	No
Fixed point?	Yes	Rotation	Reflection
Fixed point?	No	Translation	Glide reflection

Group structure

Isometries requiring an odd number of mirrors — reflection and glide reflection — always reverse left and right. The even isometries — identity, rotation, and translation — never do; they correspond to rigid motions, and form a normal subgroup

Normal subgroup

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....

of the full Euclidean group

Euclidean group

In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...

of isometries. Neither the full group nor the even subgroup are abelian

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

; for example, reversing the order of composition of two parallel mirrors reverses the direction of the translation they produce.

Proof. The identity is an isometry; nothing changes, so distance cannot change. And if one isometry cannot change distance, neither can two (or three, or more) in succession; thus the composition of two isometries is again an isometry, and the set of isometries is closed under composition. The identity isometry is also an identity for composition, and composition is associative; therefore isometries satisfy the axioms for a semigroup

Semigroup

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...

. For a group

Group (mathematics)

, we must also have an inverse for every element. To cancel a reflection, we merely compose it with itself. (Reflections are involutions.) And since every isometry can be expressed as a sequence of reflections, its inverse can be expressed as that sequence reversed. Notice that the cancellation of a pair of identical reflections reduces the number of reflections by an even number, preserving the parity of the sequence; also notice that the identity has even parity. Therefore all isometries form a group, and even isometries a subgroup. (Odd isometries do not include the identity, so are not a subgroup.) This subgroup is a normal subgroup, because sandwiching an even isometry between two odd ones yields an even isometry. ∎

Since the even subgroup is normal, it is the kernel

Kernel (algebra)

In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...

of a homomorphism

Homomorphism

In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...

to a quotient group

Quotient group

In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...

, where the quotient is isomorphic to a group consisting of a reflection and the identity. However the full group is not a direct product

Direct product of groups

In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...

, but only a semidirect product

Semidirect product

In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...

, of the even subgroup and the quotient group.

Composition

Composition of isometries mixes kinds in assorted ways. We can think of the identity as either two mirrors or none; either way, it has no effect in composition. And two reflections give either a translation or a rotation, or the identity (which is both, in a trivial way). Reflection composed with either of these could cancel down to a single reflection; otherwise it gives the only available three-mirror isometry, a glide reflection. A pair of translations always reduces to a single translation; so the challenging cases involve rotations. We know a rotation composed with either a rotation or a translation must produce an even isometry. Composition with translation produces another rotation (by the same amount, with shifted fixed point), but composition with rotation can yield either translation or rotation. It is often said that composition of two rotations produces a rotation, and Euler proved a theorem to that effect in 3D; however, this is only true for rotations sharing a fixed point.

Translation, rotation, and orthogonal subgroups

We thus have two new kinds of isometry subgroups: all translations, and rotations sharing a fixed point. Both are subgroups of the even subgroup, within which translations are normal. Because translations are a normal subgroup, we can factor them out leaving the subgroup of isometries with a fixed point, the orthogonal group

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

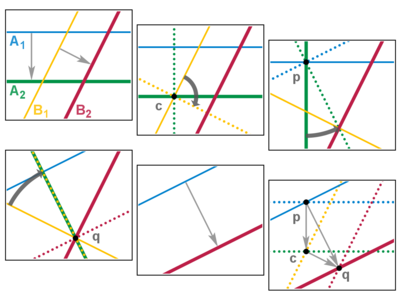
Proof. If two rotations share a fixed point, then we can swivel the mirror pair of the second rotation to cancel the inner mirrors of the sequence of four (two and two), leaving just the outer pair. Thus the composition of two rotations with a common fixed point produces a rotation by the sum of the angles about the same fixed point.

If two translations are parallel, we can slide the mirror pair of the second translation to cancel the inner mirror of the sequence of four, much as in the rotation case. Thus the composition of two parallel translations produces a translation by the sum of the distances in the same direction. Now suppose the translations are not parallel, and that the mirror sequence is A₁, A₂ (the first translation) followed by B₁, B₂ (the second). Then A₂ and B₁ must cross, say at c; and, reassociating, we are free to pivot this inner pair around c. If we pivot 90°, an interesting thing happens: now A₁ and A₂′ intersect at a 90° angle, say at p, and so do B₁′ and B₂, say at q. Again reassociating, we pivot the first pair around p to make B₂″ pass through q, and pivot the second pair around q to make A₁″ pass through p. The inner mirrors now coincide and cancel, and the outer mirrors are left parallel. Thus the composition of two non-parallel translations also produces a translation. Also, the three pivot points form a triangle whose edges give the head-to-tail rule of vector addition: 2(p c) + 2(c q) = 2(p q). ∎

Nested group construction

The subgroup structure suggests another way to compose an arbitrary isometry:

Pick a fixed point, and a mirror through it.

If the isometry is odd, use the mirror; otherwise do not.
If necessary, rotate around the fixed point.
If necessary, translate.

This works because translations are a normal subgroup of the full group of isometries, with quotient the orthogonal group; and rotations about a fixed point are a normal subgroup of the orthogonal group, with quotient a single reflection.

Discrete subgroups

The subgroups discussed so far are not only infinite, they are also continuous (Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s). Any subgroup containing at least one non-zero translation must be infinite, but subgroups of the orthogonal group can be finite. For example, the symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

of a regular pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

consist of rotations by integer multiples of 72° (360° / 5), along with reflections in the five mirrors which perpendicularly bisect the edges. This is a group, D₅, with 10 elements. It has a subgroup, C₅, of half the size, omitting the reflections. These two groups are members of two families, D_n and C_n, for any n > 1. Together, these families constitute the rosette group

Point group

In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...

s.

Translations do not fold back on themselves, but we can take integer multiples of any finite translation, or sums of multiples of two such independent translations, as a subgroup. These generate the lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

of a periodic tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

of the plane.

We can also combine these two kinds of discrete groups — the discrete rotations and reflections around a fixed point and the discrete translations — to generate the frieze group

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s and wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s. Curiously, only a few of the fixed-point groups are found to be compatible

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

with discrete translations. In fact, lattice compatibility imposes such a severe restriction that, up to isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

, we have only 7 distinct frieze groups and 17 distinct wallpaper groups. For example, the pentagon symmetries, D₅, are incompatible with a discrete lattice of translations. (Each higher dimension also has only a finite number of such crystallographic groups, but the number grows rapidly; for example, 3D has 320 groups and 4D has 4783.)

Isometries in the complex plane

In terms of complex numbers, the isometries of the plane are addition of a complex constant (translation), multiplication by a complex constant with modulus 1 (rotation), complex conjugation (reflection in the real axis), and combinations.

External links

Plane Isometries

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.