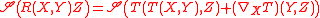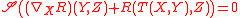In differential geometry, the notion of torsion is a manner of characterizing a twist or screw

Screw theory

Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....

 of a moving frame

Moving frame

In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...

 around a curve. The torsion of a curve

Torsion of curves

In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve...

, as it appears in the Frenet-Serret formulas

Frenet-Serret formulas

In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...

, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves (or rather the rotation of the Frenet-Serret frame about the tangent vector.) In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 measures how moving frames "roll" along a curve "without twisting."

More generally, on a differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

 equipped with an affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

 (that is, a connection

Connection (vector bundle)

In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...

 in the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

), torsion and curvature form the two fundamental invariants of the connection. In this context, torsion gives an intrinsic characterization of how tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

s twist about a curve when they are parallel transport

Parallel transport

In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...

ed; whereas curvature describes how the tangent spaces roll along the curve. Torsion may be described concretely as a tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

, or as a vector-valued

Vector-valued form

In mathematics, a vector-valued differential form on a manifold M is a differential form on M with values in a vector space V. More generally, it is a differential form with values in some vector bundle E over M. Ordinary differential forms can be viewed as R-valued differential forms...

 two-form

Two-form

In linear algebra, a two-form is another term for a bilinear form, typically used in informal discussions, or sometimes to indicate that the bilinear form is skew-symmetric....

 on the manifold. If ∇ is an affine connection on a differential manifold, then the torsion tensor is defined, in terms of vector fields X and Y, by
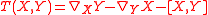
where [X,Y] is the Lie bracket of vector fields

Lie bracket of vector fields

In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...

.

Torsion is particularly useful in the study of the geometry of geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s. Given a system of parametrized geodesics, one can specify a class of affine connections having those geodesics, but differing by their torsions. There is a unique connection which absorbs the torsion, generalizing the Levi-Civita connection

Levi-Civita connection

In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...

 to other, possibly non-metric situations (such as Finsler geometry). Absorption of torsion also plays a fundamental role in the study of G-structure

G-structure

In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....

s and Cartan's equivalence method

Cartan's equivalence method

In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...

. Torsion is also useful in the study of unparametrized families of geodesics, via the associated projective connection

Projective connection

In differential geometry, a projective connection is a type of Cartan connection on a differentiable manifold.The structure of a projective connection is modeled on the geometry of projective space, rather than the affine space corresponding to an affine connection. Much like affine connections,...

. In relativity theory, such ideas have been implemented in the form of Einstein-Cartan theory.

The torsion tensor

Let M be a manifold with a connection ∇ on the tangent bundle. The torsion tensor (sometimes called the Cartan (torsion) tensor) is a vector-valued 2-form

Vector-valued form

In mathematics, a vector-valued differential form on a manifold M is a differential form on M with values in a vector space V. More generally, it is a differential form with values in some vector bundle E over M. Ordinary differential forms can be viewed as R-valued differential forms...

 defined on vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s X and Y by


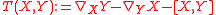
where [X,Y] is the Lie bracket

Lie bracket of vector fields

In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...

 of two vector fields. By the Leibniz rule

Leibniz rule (generalized product rule)

In calculus, the general Leibniz rule, named after Gottfried Leibniz, generalizes the product rule. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by...

, T(fX,Y) = T(X,fY) = fT(X,Y) for any smooth function

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

 f. So T is tensorial, despite being defined in terms of the non-tensorial covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

: it gives a 2-form on tangent vectors, while the covariant derivative is only defined for vector fields.

Curvature and the Bianchi identities

The curvature tensor

Riemann curvature tensor

In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...

 of ∇ is a mapping TM ∧ TM → End(TM) defined on vector fields X, Y, and Z by
Note that, for vectors at a point, this definition is independent of how the vectors are extended to vector fields away from the point (thus it defines a tensor, much like the torsion).

The Bianchi identities relate the curvature and torsion as follows. Let denote the cyclic sum

Cyclic permutation

A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...

 over X, Y, and Z. For instance,
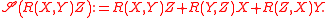
Then the following identities hold

1. Bianchi's first identity:

2. Bianchi's second identity:

Components of the torsion tensor

The components of the torsion tensor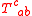 in terms of a local basis of sections

Section (fiber bundle)

In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...

 (e₁, ..., e_n) of the tangent bundle can be derived by setting X=e_i, Y=e_j and by introducing the commutator coefficients γk_ije_k := [e_i,e_j]. The components of the torsion are then


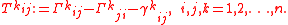
If the basis is holonomic

Holonomic

In mathematics and physics, the term holonomic may occur with several different meanings.-Holonomic basis:A holonomic basis for a manifold is a set of basis vectors ek for which all Lie derivatives vanish:[e_j,e_k]=0 \,...

 then the Lie brackets vanish, 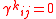. So 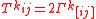. In particular (see below) while the geodesic equations

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

 determine the symmetric part of the connection, the torsion tensor determines the antisymmetric part.

The torsion form

The torsion form, an alternative characterization of torsion, applies to the frame bundle

Frame bundle

In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...

 FM of the manifold M. This principal bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

 is equipped with a connection form

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...

 ω, a gl(n)-valued one-form which maps vertical vectors to the generators of the right action in gl(n) and equivariantly intertwines the right action of GL(n) on the tangent bundle of FM with the adjoint representation on gl(n). The frame bundle also carries a canonical one-form

Solder form

In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...

 θ, with values in Rⁿ, defined at a frame u ∈ F_xM (regarded as a linear function u : Rⁿ → T_xM) by
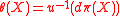
where π : FM → M is the projection mapping for the principal bundle. The torsion form is then
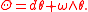
Equivalently, Θ = Dθ, where D is the exterior covariant derivative

Exterior covariant derivative

In mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection....

 determined by the connection.

The torsion form is a (horizontal) tensorial form with values in Rⁿ, meaning that under the right action of g ∈ Gl(n) it transforms equivariantly:
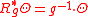
where g acts on the right-hand side through its fundamental representation on Rⁿ.

The curvature form and Bianchi identities

The curvature form

Curvature form

In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...

 is the gl(n)-valued 2-form
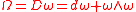
where, again, D denotes the exterior covariant derivative. In terms of the curvature form and torsion form, the corresponding Bianchi identities are

1. 
2. 

Moreover, one can recover the curvature and torsion tensors from the curvature and torsion forms as follows. At a point u of F_xM, one has
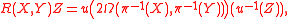
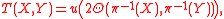
where again u : Rⁿ → T_xM is the function specifying the frame in the fibre, and the choice of lift of the vectors via π⁻¹ is irrelevant since the curvature and torsion forms are horizontal (they vanish on the ambiguous vertical vectors).

Torsion form in a frame

The torsion form may be expressed in terms of a connection form

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

 on the base manifold M, written in a particular frame of the tangent bundle (e₁,...,e_n). The connection form expresses the exterior covariant derivative of these basic sections:
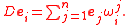
The solder form

Solder form

In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...

 for the tangent bundle (relative to this frame) is the dual basis θⁱ ∈ T^*M of the e_i, so that θi(e_j) = δⁱ_j (the Kronecker delta.) Then the torsion 2-form has components

In the rightmost expression,
are the frame-components of the torsion tensor, as given in the previous definition.

It can be easily shown that Θⁱ transforms tensorially in the sense that if a different frame
for some invertible matrix-valued function (g_i^j), then
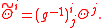
In other terms, Θ is a tensor of type (1,2) (carrying one contravariant and two covariant indices).

Alternatively, the solder form can be characterized in a frame-independent fashion as the TM-valued one-form θ on M corresponding to the identity endomorphism of the tangent bundle under the duality isomorphism End(TM) ≈ TM ⊗ T^*M. Then the torsion two-form is a section of
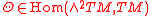
given by
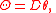
where D is the exterior covariant derivative

Exterior covariant derivative

In mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection....

. (See connection form

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

 for further details.)

Irreducible decomposition

The torsion tensor can be decomposed into two irreducible parts: a trace-free

Trace (linear algebra)

In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

 part and another part which contains the trace terms. Using the index notation

Index notation

Index notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...

, the trace of T is given by
and the trace-free part is
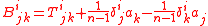
where δi_j is the Kronecker delta.

Intrinsically, one has
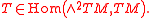
The trace of T, tr T, is an element of T^*M defined as follows. For each vector fixed X ∈ TM, T defines an element T(X) of Hom(TM, TM) via
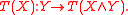
Then (tr T)(X) is defined as the trace of this endomorphism. That is,

The trace-free part of T is then
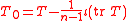
where ι denotes the interior product.

Characterizations and interpretations

Throughout this section, M is assumed to be a differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

, and ∇ a covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

 on the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

 of M unless otherwise noted.

Twisting of reference frames

In the classical differential geometry of curves

Differential geometry of curves

Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....

, the Frenet-Serret formulas

Frenet-Serret formulas

In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...

 describe how a particular moving frame (the Frenet-Serret frame) twists along a curve. In physical terms, the torsion corresponds to the angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

 of an idealized top

Top

A top is a toy that can be spun on an axis, balancing on a point. This motion is produced in the most simple forms of top by twirling the stem using the fingers. More sophisticated tops are spun by by holding the axis firmly while pulling a string or twisting a stick or pushing an auger as shown...

 pointing along the tangent of the curve.

The case of a manifold with a (metric) connection admits an analogous interpretation. Suppose that an observer is moving along a geodesic for the connection. Such an observer is ordinarily thought of as inertial since she experiences no acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

. Suppose that in addition the observer carries with herself a system of rigid straight measuring rods (a coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

). Each rod is a straight segment; a geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

. Assume that each rod is parallel transport

Parallel transport

In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...

ed along the trajectory. The fact that these rods are physically carried along the trajectory means that they are Lie-dragged, or propagated so that the Lie derivative

Lie derivative

In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...

 of each rod along the tangent vanishes. They may, however, experience torque (or torsional forces) analogous to the torque felt by the top in the Frenet-Serret frame. This force is measured by the torsion.

More precisely, suppose that the observer moves along a geodesic path γ(t) and carries a measuring rod along it. The rod sweeps out a surface as the observer travels along the path. There are natural coordinates (t,x) along this surface, where t is the parameter time taken by the observer, and x is the position along the measuring rod. The condition that the tangent of the rod should be parallel translated along the curve is


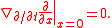
Consequently, the torsion is given by


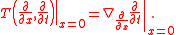
If this is not zero, then the marked points on the rod (the x = constant curves) will trace out helices instead of geodesics. They will tend to rotate around the observer. Note that for this argument it was not essential that 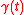is a geodesic. Any curve would work.

This interpretation of torsion plays a role in the theory of teleparallelism

Teleparallelism

Teleparallelism , was an attempt by Einstein to unify electromagnetism and gravity...

, also known as Einstein-Cartan theory, an alternative formulation of relativity theory.

The torsion of a filament

In materials science

Materials science

Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...

, and especially elasticity theory, ideas of torsion also play an important role. One problem models the growth of vines, focusing on the question of how vines manage to twist around objects. The vine itself is modeled as a pair of elastic filaments twisted around one another. In its energy-minimizing state, the vine naturally grows in the shape of a helix. But the vine may also be stretched out to maximize its extent (or length). In this case, the torsion of the vine is related to the torsion of the pair of filaments (or equivalently the surface torsion of the ribbon connecting the filaments), and it reflects the difference between the length-maximizing (geodesic) configuration of the vine and its energy-minimizing configuration.

Torsion and vorticity

In fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

, torsion is naturally associated to vortex lines.

Geodesics and the absorption of torsion

Suppose that γ(t) is a curve on M. Then γ is an affinely parametrized geodesic provided that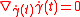
for all time t in the domain of γ. (Here the dot denotes differentiation with respect to t, which associates with γ the tangent vector pointing along it.) Each geodesic is uniquely determined by its initial tangent vector at time t=0, .

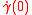One application of the torsion of a connection involves the geodesic spray of the connection: roughly the family of all affinely parametrized geodesics. Torsion is the ambiguity of classifying connections in terms of their geodesic sprays:

• Two connections ∇ and ∇′ which have the same affinely parametrized geodesics (i.e., the same geodesic spray) differ only by torsion.

More precisely, if X and Y are a pair of tangent vectors at p ∈ M, then let
be the difference of the two connections, calculated in terms of arbitrary extensions of X and Y away from p. By the Leibniz product rule, one sees that Δ does not actually depend on how X and Y are extended (so it defines a tensor on M). Let S and A be the symmmetric and alternating parts of Δ:
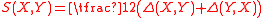
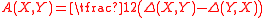
Then

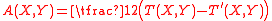• is the difference of the torsion tensors.
• ∇ and ∇′ define the same families of affinely parametrized geodesics if and only if S(X,Y) = 0.

In other words, the symmetric part of the difference of two connections determines whether they have the same parametrized geodesics, whereas the skew part of the difference is determined by the relative torsions of the two connections. Another consequence is:

• Given any affine connection ∇, there is a unique torsion-free connection ∇′ with the same family of affinely parametrized geodesics.

This is a generalization of the fundamental theorem of Riemannian geometry

Fundamental theorem of Riemannian geometry

In Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold there is a unique torsion-free metric connection, called the Levi-Civita connection of the given metric...

 to general affine (possibly non-metric) connections. Picking out the unique connection subordinate to a family of parametrized geodesics is known as absorption of torsion, and it is one of the stages of Cartan's equivalence method

Cartan's equivalence method

In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...

.

See also

• Curvature tensor
  Curvature tensor
  In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
  
  
• Contortion tensor
• Levi-Civita connection
  Levi-Civita connection
  In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
  
  
• Torsion of curves
  Torsion of curves
  In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve...
  
  

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.