A
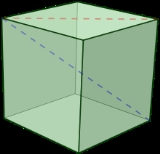
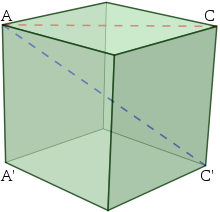
diagonal is a line joining two nonconsecutive vertices of a
polygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
or
polyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
. Informally, any sloping line is called diagonal. The word "diagonal" derives from the
GreekGreek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
διαγώνιος (
diagonios), from
dia- ("through", "across") and
gonia ("angle", related to
gony "knee"); it was used by both Strabo and Euclid to refer to a line connecting two vertices of a
rhombusIn Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
or
cuboidIn geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
, and later adopted into Latin as
diagonus ("slanting line").
In
mathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in addition to its geometric meaning, a diagonal is also used in matrices to refer to a set of entries along a diagonal line.
Non-mathematical uses
In
engineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, a
diagonal brace is a beam used to brace a rectangular structure (such as
scaffoldingScaffolding is a temporary structure used to support people and material in the construction or repair of buildings and other large structures. It is usually a modular system of metal pipes or tubes, although it can be from other materials...
) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliersDiagonal pliers are pliers intended for the cutting of wire . They are sometimes called side cutting pliers or side cutters, although these terms are shared by other pliers designs, such as lineman's pliers, and may lead to confusion...
are wire-cutting pliers whose cutting edges intersect the joint rivet at an angle or "on a diagonal".
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.
Polygons
As applied to a
polygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, a
diagonal is a
line segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
joining any two non-consecutive vertices. Therefore, a
quadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
has two diagonals, joining opposite pairs of vertices. For any
convex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any
n-sided polygon (
n ≥ 3),
convexIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
or concave, has
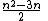
diagonals, as each vertex has diagonals to all other vertices except itself and the two adjacent vertices, or
n − 3 diagonals.
| Sides | Diagonals |
| 3 |
0 |
| 4 |
2 |
| 5 |
5 |
| 6 |
9 |
| 7 |
14 |
| 8 |
20 |
| 9 |
27 |
| 10 |
35 |
|
| Sides | Diagonals |
| 11 |
44 |
| 12 |
54 |
| 13 |
65 |
| 14 |
77 |
| 15 |
90 |
| 16 |
104 |
| 17 |
119 |
| 18 |
135 |
|
| Sides | Diagonals |
| 19 |
152 |
| 20 |
170 |
| 21 |
189 |
| 22 |
209 |
| 23 |
230 |
| 24 |
252 |
| 25 |
275 |
| 26 |
299 |
|
| Sides | Diagonals |
| 27 |
324 |
| 28 |
350 |
| 29 |
377 |
| 30 |
405 |
| 31 |
434 |
| 32 |
464 |
| 33 |
495 |
| 34 |
527 |
|
| Sides | Diagonals |
| 35 |
560 |
| 36 |
594 |
| 37 |
629 |
| 38 |
665 |
| 39 |
702 |
| 40 |
740 |
| 41 |
779 |
| 42 |
819 |
|
Matrices
In the case of a square matrix, the
main or
principal diagonal is the diagonal line of entries running from the top-left corner to the bottom-right corner. For a matrix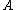
with row index specified by
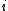and column index specified by
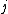, these would be entries
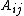with
. For example, the
identity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
can be defined as having entries of 1 on the main diagonal and zeroes elsewhere:
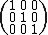
The top-right to bottom-left diagonal is sometimes described as the
minor diagonal or
antidiagonal. The
off-diagonal entries are those not on the main diagonal. A
diagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
is one whose off-diagonal entries are all zero.
A
superdiagonal entry is one that is directly above and to the right of the main diagonal. Just as diagonal entries are those
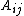with
, the superdiagonal entries are those with
. For example, the non-zero entries of the following matrix all lie in the superdiagonal: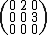
Likewise, a
subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry
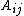with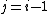
. General matrix diagonals can be specified by an index
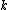measured relative to the main diagonal: the main diagonal has
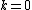; the superdiagonal has
; the subdiagonal has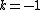
; and in general, the
-diagonal consists of the entries
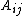with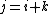
.
Geometry
By analogy, the
subsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the
Cartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X×
X of any set
X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the identity relation. This plays an important part in geometry; for example, the
fixed pointIn mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of a
mappingIn mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
F from
X to itself may be obtained by intersecting the graph of
F with the diagonal.
In geometric studies, the idea of intersecting the diagonal
with itself is common, not directly, but by perturbing it within an
equivalence class. This is related at a deep level with the
Euler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
and the zeros of
vector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s. For example, the
circleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
S1 has
Betti numberIn algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-
torusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
S1xS
1 and observe that it can move
off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed point theorem; the self-intersection of the diagonal is the special case of the identity function.
External links
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
.
- Diagonal of a matrix from MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
.