
Real projective plane
Encyclopedia
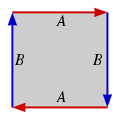 The fundamental polygon Fundamental polygon In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges.... of the projective plane. |
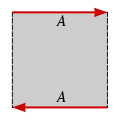 The Möbius strip Möbius strip The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface... with a single edge, can be closed into a projective plane by gluing opposite open edges together. |
 In comparison the Klein bottle Klein bottle In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a... is a Möbius strip closed into a cylinder. |
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the real projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
is an example of a compact non-orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
two-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, that is, a one-sided surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
. It cannot be embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in our usual three-dimensional space without intersecting itself. It has basic applications to geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin.
The plane is also often described topologically, in terms of a construction based on the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
: if one could glue the (single) edge of the Möbius strip to itself in the correct direction, one would obtain the projective plane. (This cannot be done in our three-dimensional space.) Equivalently, gluing a disk along the boundary of the Möbius strip gives the projective plane. Topologically, it has Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
1, hence a demigenus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
(non-orientable genus, Euler genus) of 1.
Since the Möbius strip, in turn, can be constructed from a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
by gluing two of its sides together, the real projective plane can thus be represented as a unit square (that is, [0,1] ×
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
[0,1] ) with its sides identified by the following equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s:
~ (1, 1 − y) for 0 ≤ y ≤ 1
and
~ (1 − x, 1) for 0 ≤ x ≤ 1,
as in the diagram on the right.
Examples
TopologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
is not concerned with flatness, and the real projective plane may be twisted up and placed in the Euclidean plane or 3-space in many different ways. Some of the more important examples are described below.
The projective plane cannot be embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
(that is without intersection) in three-dimensional Euclidean
Euclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
space. The proof that the projective plane does not embed in three-dimensional Euclidean space goes like this: Assume that it does embed, it would bound a compact region in three-dimensional Euclidean space by the generalized Jordan curve theorem
Jordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
. The outward-pointing unit normal vector field would then give an orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of the boundary manifold, but the boundary manifold would be projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, which is not orientable. This is a contradiction, and so our assumption that it does embed must have been false.
The projective sphere
Consider a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, and let the great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s of the sphere be "lines", and let pairs of antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s be "points". It is easy to check that this system obeys the axioms required of a projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
:
- any pair of distinct great circles meet at a pair of antipodal points; and
- any two distinct pairs of antipodal points lie on a single great circle.
If we identify each point on the sphere with its antipodal point, then we get a representation of the real projective plane in which the "points" of the projective plane really are points. This means that the projective plane is the quotient space of the sphere obtained by partitioning the sphere into equivalence classes under the equivalence relation ~, where x ~ y if
If
If is a conjunction that can introduce a conditional clause.If may also refer to:-Music:* If , a 1951 hit song by Perry Como.* If , 1970s British progressive jazz-rock band* If...
y = −x. This quotient space of the sphere is homeomorphic with the collection of all lines passing through the origin in R3.
The quotient map from the sphere onto the real projective plane is in fact a two sheeted (i.e. two-to-one) covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
. It follows that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the real projective plane is the cyclic group of order 2, i.e. integers modulo 2. One can take the loop AB from the figure above to be the generator.
The projective hemisphere
Because the real projective plane covers the sphere twice, it may be represented as a hemisphere around whose rim opposite points are similarly identified.Boy surface – an immersion
The projective plane can be immersed (local neighbourhoods do not have self-intersections) in 3-space. Boy's surfaceBoy's surface
In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...
is an example of an immersion.
Polyhedral examples must have at least nine faces.
Roman surface

Roman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
is a more degenerate map of the projective plane into 3-space, containing a cross-cap
Cross-cap
In mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
.

Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
representation is the tetrahemihexahedron
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....
, which has the same general form as Steiner's Roman Surface, shown to the right.
Hemi polyhedra
Looking in the opposite direction, certain abstract regular polytopes — hemi-cube, hemi-dodecahedronHemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
, and hemi-icosahedron
Hemi-icosahedron
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing...
— can be constructed as regular figures in the projective plane; see also projective polyhedra.
Planar projections
Various planar (flat) projections or mappings of the projective plane have been described. In 1874 Klein described the mapping
Central projection of the projective hemisphere onto a plane yields the usual infinite projective plane, described below.
Homogeneous coordinates
The points in the plane can be represented by homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. A point has homogeneous coordinates [x : y : z], where the coordinates [x : y : z] and [tx : ty : tz] are considered to represent the same point, for all nonzero values of t. The points with coordinates [x : y : 1] are the usual real plane, called the finite part of the projective plane, and points with coordinates [x : y : 0], called points at infinity or ideal points, constitute a line called the line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
. (The homogeneous coordinates [0 : 0 : 0] do not represent any point.)
The lines in the plane can also be represented by homogeneous coordinates. A projective line corresponding to the plane ax + by + c = 0 in R3 has the homogeneous coordinates (a : b : c). Thus, these coordinates have the equivalence relation (a : b : c) = (da : db : dc) for all nonzero values of d. Hence a different equation of the same line dax + dby + dc = 0 gives the same homogeneous coordinates.
A point [x : y : z] lies on a line (a : b : c) if ax + by + c = 0.
Therefore, lines with coordinates (a : b : c) where a, b are not both 0 correspond to the lines in the usual real plane, because they contain points that are not at infinity. The line with coordinates (0 : 0 : 1) is the line at infinity, since the only points on it are those with z = 0.
The flat projective plane

In the projective plane P2, a point x is represented by the homogeneous coordinate (x1, x2, x3). If we think of (x1, x2, x3) as a point in real space R3 with the third value of the homogeneous coordinate as a value in the z direction, then P2 can be visualized as R3.
Points, rays, lines, and planes
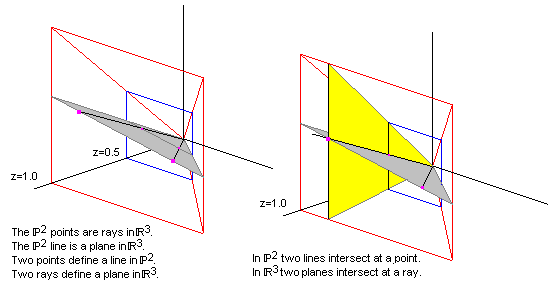
A line in P2 can be represented by the equation ax + by + c = 0. If we treat a, b, and c as the column vector ℓ and x, y, 1 as the column vector x then the equation above can be written in matrix form as:
- xTℓ = 0 or ℓTx = 0.
Using vector notation we may instead write
- x ⋅ ℓ = 0 or ℓ ⋅ x = 0.
The equation k(xTℓ) = 0 (which k is a non-zero scalar) sweeps out a plane that goes through zero in R3 and k(x) sweeps out a ray, again going through zero. The plane and ray are subspaces
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
in R3, which always go through zero.
Ideal points

In P2 the equation of a line is ax + by + c = 0 and this equation can represent a line on any plane parallel to the x, y plane by multiplying the equation by k.
If z = 1 we have a normalized homogeneous coordinate. All points that have z = 1 create a plane. Let's pretend we are looking at that plane (from a position further out along the z axis and looking back towards the origin) and there are two parallel lines drawn on the plane. From where we are standing (given our visual capabilities) we can see only so much of the plane, which we represent as the area outlined in red in the diagram. If we walk away from the plane along the z axis, (still looking backwards towards the origin), we can see more of the plane. In our field of view original points have moved. We can reflect this movement by dividing the homogeneous coordinate by a constant. In the image to the right we have divided by 2 so the z value now becomes 0.5. If we walk far enough away what we are looking at becomes a point in the distance. As we walk away we see more and more of the parallel lines. The lines will meet at a line at infinity (a line that goes through zero on the plane at z = 0). Lines on the plane when z = 0 are ideal points. The plane at z = 0 is the line at infinity.
The homogeneous point (0, 0, 0) is where all the real points go when you're looking at the plane from an infinite distance, a line on the z = 0 plane is where parallel lines intersect.
Duality
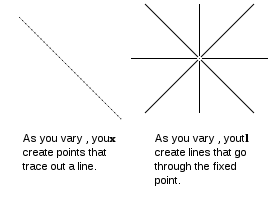
In the equation xTℓ = 0 there are two column vectors. You can keep either constant and vary the other. If we keep the point constant x and vary the coefficients ℓ we create new lines that go through the point. If we keep the coefficients constant and vary the points that satisfy the equation we create a line. We look upon x as a point because the axes we are using are x, y, and z. If we instead plotted the coefficients using axis marked a, b, c points would become lines and lines would become points. If you prove something with the data plotted on axis marked x, y, and z the same argument can be used for the data plotted on axis marked a, b, and c. That is duality.
Lines joining points and intersection of lines (using duality)
The equation xTℓ = 0 calculates the inner productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of two column vectors. The inner product of two vectors is zero if the vectors are orthogonal. To find the line between the points x1 and x2 you must find the column vector ℓ that satisfies the equations x1Tℓ = 0 and x2Tℓ = 0, that is we must find a column vector ℓ that is orthogonal to x1 and x2. In the case of P2, the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
will find such a vector. The line joining two points is given by the equation x1 × x2. To find the intersection of two lines you look to duality. If you plot ℓ in the coefficient space you get rays. To find the point x that is orthogonal to the two rays you find the cross product. That is ℓ1 × ℓ2.
While the cross product works in P2, it is not well-defined in arbitrary dimensions. However, this pair of equations is satisfied by

Embedding into 4-dimensional space
The projective plane embeds into 4-dimensional Euclidean space. Consider to be the quotient
to be the quotientQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of the two-sphere
 by the antipodal relation
by the antipodal relation  . Consider the function
. Consider the function  given by
given by  . This map restricts to a map whose domain is
. This map restricts to a map whose domain is  and, since it is a purely quadratic polynomial, it can be factorised to give a map
and, since it is a purely quadratic polynomial, it can be factorised to give a map  . Moreover, this map is an embedding. Notice that this embedding admits a projection into
. Moreover, this map is an embedding. Notice that this embedding admits a projection into  which is the Roman surface
which is the Roman surfaceRoman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
.
Higher non-orientable surfaces
By glueing together projective planes successively we get non-orientable surfaces of higher demigenusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
. The glueing process consists of cutting out a little disk from each surface and identifying (glueing) their boundary circles. Glueing two projective planes creates the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
.
The article on the fundamental polygon
Fundamental polygon
In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....
describes the higher non-orientable surfaces.

