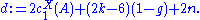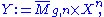Gromov-Witten invariant
Encyclopedia
In mathematics
, specifically in symplectic topology
and algebraic geometry
, Gromov–Witten (GW) invariants are rational number
s that, in certain situations, count pseudoholomorphic curve
s meeting prescribed conditions in a given symplectic manifold
. The GW invariants may be packaged as a homology
or cohomology
class in an appropriate space, or as the deformed cup product
of quantum cohomology
. These invariants have been used to distinguish symplectic manifolds that were previously indistinguishable. They also play a crucial role in closed type IIA string theory
. They are named for Mikhail Gromov and Edward Witten
.
The rigorous mathematical definition of Gromov–Witten invariants is lengthy and difficult, so it is treated separately in the stable map
article. This article attempts a more intuitive explanation of what the invariants mean, how they are computed, and why they are important.
Now we define the Gromov-Witten invariants are associated to the 4-tuple: (X, A, g, n). Let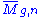 : the Deligne–Mumford moduli space of curves of genus g with n marked points and
: the Deligne–Mumford moduli space of curves of genus g with n marked points and 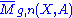 denote the moduli space of stable map
denote the moduli space of stable map
s into X of class A, for some chosen almost complex structure
J on X compatible with its symplectic form. The elements of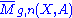 are of the form:
are of the form:
where C is a (not necessarily stable) curve with n marked points x1, ..., xn and f : C → X is pseudoholomorphic. The moduli space has real dimension
Let
denote the stabilization
of the curve. Let
which has real dimension 6g - 6 + 2 k n. There is an evaluation map
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Gromov–Witten (GW) invariants are rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s that, in certain situations, count pseudoholomorphic curve
Pseudoholomorphic curve
In mathematics, specifically in topology and geometry, a pseudoholomorphic curve is a smooth map from a Riemann surface into an almost complex manifold that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of...
s meeting prescribed conditions in a given symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. The GW invariants may be packaged as a homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
or cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
class in an appropriate space, or as the deformed cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
of quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
. These invariants have been used to distinguish symplectic manifolds that were previously indistinguishable. They also play a crucial role in closed type IIA string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. They are named for Mikhail Gromov and Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
.
The rigorous mathematical definition of Gromov–Witten invariants is lengthy and difficult, so it is treated separately in the stable map
Stable map
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find...
article. This article attempts a more intuitive explanation of what the invariants mean, how they are computed, and why they are important.
Definition
Consider the following:- X: a closedClosed manifoldIn mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
symplectic manifold of dimension 2k, - A: a 2-dimensional homology class in X,
- g: a non-negative integer,
- n: a non-negative integer.
Now we define the Gromov-Witten invariants are associated to the 4-tuple: (X, A, g, n). Let
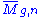 : the Deligne–Mumford moduli space of curves of genus g with n marked points and
: the Deligne–Mumford moduli space of curves of genus g with n marked points and 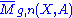 denote the moduli space of stable map
denote the moduli space of stable mapStable map
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find...
s into X of class A, for some chosen almost complex structure
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
J on X compatible with its symplectic form. The elements of
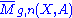 are of the form:
are of the form:
-
-
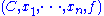 ,
,
-
where C is a (not necessarily stable) curve with n marked points x1, ..., xn and f : C → X is pseudoholomorphic. The moduli space has real dimension
Let
denote the stabilization
Stable map
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find...
of the curve. Let
which has real dimension 6g - 6 + 2 k n. There is an evaluation map
-
-
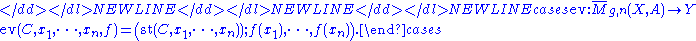
The evaluation map sends the fundamental classFundamental classIn mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
of M to a d-dimensional rational homology class in Y, denoted
In a sense, this homology class is the Gromov–Witten invariant of X for the data g, n, and A. It is an invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the symplectic isotopy class of the symplectic manifold X.
To interpret the Gromov–Witten invariant geometrically, let be a homology class in
be a homology class in 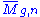 and
and  homology classes in
homology classes in 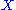 , such that the sum of the codimensions of
, such that the sum of the codimensions of 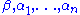 equals
equals 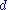 . These induce homology classes in
. These induce homology classes in 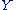 by the Künneth formula. Let
by the Künneth formula. Let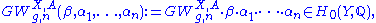
where denotes the intersection productIntersection theoryIn mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
denotes the intersection productIntersection theoryIn mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
in the rational homology of . This is a rational number, the Gromov–Witten invariant for the given classes. This number gives a "virtual" count of the number of pseudoholomorphic curves (in the class
. This is a rational number, the Gromov–Witten invariant for the given classes. This number gives a "virtual" count of the number of pseudoholomorphic curves (in the class 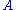 , of genus
, of genus 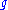 , with domain in the
, with domain in the 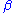 -part of the Deligne–Mumford space) whose
-part of the Deligne–Mumford space) whose  marked points are mapped to cycles representing the
marked points are mapped to cycles representing the 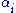 .
.
Put simply, a GW invariant counts how many curves there are that intersect chosen submanifolds of
chosen submanifolds of 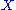 . However, due to the "virtual" nature of the count, it need not be a natural number, as one might expect a count to be. For the space of stable maps is an orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
. However, due to the "virtual" nature of the count, it need not be a natural number, as one might expect a count to be. For the space of stable maps is an orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
, whose points of isotropy can contribute noninteger values to the invariant.
There are numerous variations on this construction, in which cohomology is used instead of homology, integration replaces intersection, Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es pulled back from the Deligne–Mumford space are also integrated, etc.
Computational techniques
Gromov–Witten invariants are generally difficult to compute. While they are defined for any generic almost complex structureAlmost complex manifoldIn mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
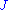 , for which the linearizationLinearizationIn mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
, for which the linearizationLinearizationIn mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
 of the
of the  operator is surjective, they must actually be computed with respect to a specific, chosen
operator is surjective, they must actually be computed with respect to a specific, chosen  . It is most convenient to choose
. It is most convenient to choose 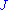 with special properties, such as nongeneric symmetries or integrability. Indeed, computations are often carried out on Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
with special properties, such as nongeneric symmetries or integrability. Indeed, computations are often carried out on Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s using the techniques of algebraic geometry.
However, a special may induce a nonsurjective
may induce a nonsurjective  and thus a moduli space of pseudoholomorphic curves that is larger than expected. Loosely speaking, one corrects for this effect by forming from the cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
and thus a moduli space of pseudoholomorphic curves that is larger than expected. Loosely speaking, one corrects for this effect by forming from the cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, called the obstruction bundle, and then realizing the GW invariant as the integral of the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the obstruction bundle. Making this idea precise requires significant technical argument using Kuranishi structures or polyfolds.
The main computational technique is localization. This applies when is toricToric geometryIn algebraic geometry, a toric variety or torus embedding is a normal variety containing an algebraic torus as a dense subset, such that the action of the torus on itself extends to the whole variety.-The toric variety of a fan:...
is toricToric geometryIn algebraic geometry, a toric variety or torus embedding is a normal variety containing an algebraic torus as a dense subset, such that the action of the torus on itself extends to the whole variety.-The toric variety of a fan:...
, meaning that it is acted upon by a complex torus, or at least locally toric. Then one can use the Atiyah–Bott fixed-point theoremAtiyah–Bott fixed-point theoremIn mathematics, the Atiyah–Bott fixed-point theorem, proven by Michael Atiyah and Raoul Bott in the 1960s, is a general form of the Lefschetz fixed-point theorem for smooth manifolds M , which uses an elliptic complex on M...
, of AtiyahMichael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and BottRaoul BottRaoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
, to reduce, or localize, the computation of a GW invariant to an integration over the fixed-point locus of the action.
Another approach is to employ symplectic surgeries to relate to one or more other spaces whose GW invariants are more easily computed. Of course, one must first understand how the invariants behave under the surgeries. For such applications one often uses the more elaborate relative GW invariants, which count curves with prescribed tangency conditions along a symplectic submanifold of
to one or more other spaces whose GW invariants are more easily computed. Of course, one must first understand how the invariants behave under the surgeries. For such applications one often uses the more elaborate relative GW invariants, which count curves with prescribed tangency conditions along a symplectic submanifold of 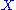 of real codimension two.
of real codimension two.
Related invariants and other constructions
The Gromov–Witten invariants are closely related to a number of other concepts in geometry, including the Donaldson invariants and Seiberg–Witten invariantSeiberg–Witten invariantIn mathematics, Seiberg–Witten invariants are invariants of compact smooth 4-manifolds introduced by , using the Seiberg–Witten theory studied by during their investigations of Seiberg–Witten gauge theory....
s. For compact symplectic four-manifolds, Clifford TaubesClifford TaubesClifford Henry Taubes is the William Petschek Professor of Mathematics at Harvard University and works in gauge field theory, differential geometry, and low-dimensional topology.-Early career:Taubes received his Ph.D...
showed that a variant of the Gromov–Witten invariants (see Taubes's Gromov invariantTaubes's Gromov invariantIn mathematics, the Gromov invariant of Clifford Taubes counts embedded pseudoholomorphic curves in a symplectic 4-manifold...
) are equivalent to the Seiberg–Witten invariants. They are conjectured to contain the same information as Donaldson–Thomas invariants and Gopakumar–Vafa invariants, both of which are integer-valued.
GW invariants can also be defined using the language of algebraic geometry. In some cases, GW invariants agree with classical enumerative invariants of algebraic geometry. However, in general GW invariants enjoy one important advantage over the enumerative invariants, namely the existence of a composition law which describes how curves glue. The GW invariants can be bundled up into the quantum cohomology ring of the manifold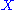 , which is a deformation of the ordinary cohomology. The composition law of GW invariants is what makes the deformed cup product associative.
, which is a deformation of the ordinary cohomology. The composition law of GW invariants is what makes the deformed cup product associative.
The quantum cohomology ring is known to be isomorphic to the symplectic Floer homologyFloer homologyFloer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
with its pair-of-pants product.
Application in physics
Gromov–Witten invariants are of interest in string theory, a branch of physics that attempts to unify general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In this theory, everything in the universe, beginning with the elementary particleElementary particleIn particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s, is made of tiny stringString (physics)A string is a hypothetical vibrating one-dimensional sub-atomic structure and one of the main objects of study in string theory, a branch of theoretical physics. There are different string theories, many of which are unified by M-theory. A string is an object with a one-dimensional spatial extent,...
s. As a string travels through spacetime it traces out a surface, called the worldsheet of the string. Unfortunately, the moduli space of such parametrized surfaces, at least a priori, is infinite-dimensional; no appropriate measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on this space is known, and thus the path integralsPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of the theory lack a rigorous definition.
The situation improves in the variation known as closed A model topological string theoryTopological string theoryIn theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...
. Here there are six spacetime dimensions, which constitute a symplectic manifold, and it turns out that the worldsheets are necessarily parametrized by pseudoholomorphic curves, whose moduli spaces are only finite-dimensional. Gromov–Witten invariants, as integrals over these moduli spaces, are then path integrals of the theory. In particular, the free energyHelmholtz free energyIn thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
of the A model at genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g is the generating functionGenerating functionIn mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the genus g Gromov–Witten invariants.-
-