
Invariant (mathematics)
Encyclopedia
In mathematics
, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries
of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation
is a property that is constant on each equivalence class.
Invariants are used in diverse areas of mathematics such as geometry
, topology
and algebra
. Some important classes of transformations are defined by an invariant they leave unchanged, for example conformal map
s are defined as transformations of the plane that preserve angles. The discovery of invariants is an important step in the process of classifying mathematical objects.
– is associated with the set and is invariant under the process of counting.
An identity is an equation that remains true for all values of its variables. There are also inequalities that remain true when the value of their variables change.
Another simple example of invariance is that the distance
between two points on a number line
is not changed by adding
the same quantity to both numbers. On the other hand multiplication
does not have this property so distance is not invariant under multiplication.
Angle
s and ratio
s of distances are invariant under scalings
, rotation
s, translation
s and reflection
s. These transformations produce similar
shapes, which is the basis of trigonometry
. All circles are similar therefore they can be transformed into each other and the ratio of the circumference
to the diameter
is invariant and equal to pi
.
 Note that the elements of S are not fixed
Note that the elements of S are not fixed
, but rather the set S is fixed in the power set of U.
For example, a circle
is an invariant subset of the plane under a rotation
about the circle’s center. Further, a conical surface
is invariant as a set under a homothety of space.
An invariant set of an operation T is also said to be stable under T. For example, the normal subgroup
s that are so important in group theory
are those subgroup
s that are stable under the inner automorphism
s of the ambient group.
s, presentations, and deformation.
Very frequently one will have a group acting on a set X and ask for what objects in an associated set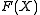 are invariant. For example, rotation in the plane about a point leaves the point that it is rotating about invariant, while translation in the plane does not leave any points invariant, but does leave all lines parallel to the direction of translation invariant as lines. Formally, define the set of lines in the plane P as
are invariant. For example, rotation in the plane about a point leaves the point that it is rotating about invariant, while translation in the plane does not leave any points invariant, but does leave all lines parallel to the direction of translation invariant as lines. Formally, define the set of lines in the plane P as 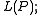 then a rigid motion of the plane takes lines to lines – the group of rigid motions acts on the set of lines – and one may ask which lines are unchanged by an action.
then a rigid motion of the plane takes lines to lines – the group of rigid motions acts on the set of lines – and one may ask which lines are unchanged by an action.
More importantly, one may define a function on a set, such as "radius of a circle in the plane" and then ask if this function is invariant under a group action, such as rigid motions.
Dual to the notion of invariants are coinvariants, also known as orbits, which formalizes the notion of congruence
: objects which can be taken to each other by a group action. For example, under the group of rigid motions of the plane, the perimeter of a triangle is an invariant, while the set of triangles congruent to a given triangle is a coinvariant.
These are connected as follows: invariants are constant on coinvariants (for example, congruent triangles have the same perimeter), while two objects which agree in the value of one invariant may or may not be congruent (two triangles with the same perimeter need not be congruent). In classification problems, one seeks to find a complete set of invariants
, such that if two objects have the same values for this set of invariants, they are congruent. For example, triangles such that all three sides are equal are congruent, via SSS congruence, and thus the length of all three sides forms a complete set of invariants for triangles.
of a cell complex is defined as the alternating sum of the number of cells in each dimension. One may forget the cell complex structure and look only at the underlying topological space (the manifold) – as different cell complexes give the same underlying manifold, one may ask if the function is independent of choice of presentation, in which case it is an intrinsically defined invariant. This is the case for the Euler characteristic, and a general method for defining and computing invariants is to define them for a given presentation and then show that they are independent of the choice of presentation. Note that there is no notion of a group action in this sense.
The most common examples are:
and differential geometry, one may ask if the property is unchanged under perturbation – if an object is constant on families or invariant under change of metric, for instance.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
is a property that is constant on each equivalence class.
Invariants are used in diverse areas of mathematics such as geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. Some important classes of transformations are defined by an invariant they leave unchanged, for example conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s are defined as transformations of the plane that preserve angles. The discovery of invariants is an important step in the process of classifying mathematical objects.
Simple examples
The most fundamental example of invariance is expressed in our ability to count. For a finite collection of objects of any kind, there appears to be a number to which we invariably arrive regardless of how we count the objects in the set. The quantity – a cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
– is associated with the set and is invariant under the process of counting.
An identity is an equation that remains true for all values of its variables. There are also inequalities that remain true when the value of their variables change.
Another simple example of invariance is that the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between two points on a number line
Number line
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
is not changed by adding
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
the same quantity to both numbers. On the other hand multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
does not have this property so distance is not invariant under multiplication.
Angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s and ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of distances are invariant under scalings
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
s, translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s and reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s. These transformations produce similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
shapes, which is the basis of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
. All circles are similar therefore they can be transformed into each other and the ratio of the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
to the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
is invariant and equal to pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
More advanced examples
Some more complicated examples:- The real part and the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
are invariant under complex conjugation. - The degree of a polynomial is invariant under linear change of variables.
- The dimension of a topological object is invariant under homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. - The number of fixed pointsFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of a dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is invariant under many mathematical operations. - Euclidean distance is invariant under orthogonal transformationsOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. - Euclidean areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
is invariant under a linear map with determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 (see Equi-areal maps). - The cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
is invariant under projective transformations. - The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, and eigenvectors and eigenvalues of a square matrix are invariant under changes of basis, in a word, the spectra of a matrix is invariant to the change of basis. - Invariants of tensorsInvariants of tensorsIn mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
. - The singular values of a matrix are invariant under orthogonal transformations.
- Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
is invariant under translations. - The varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is invariant under translations of the realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
line; hence the variance of a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is unchanged by the addition of a constant to it. - The fixed pointsFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of a transformation are the elements in the domain invariant under the transformation. They may, depending on the application, be called symmetricSymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
with respect to that transformation. For example, objects with translational symmetryTranslational symmetryIn geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
are invariant under certain translations. - The integral
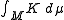 of the Gaussian curvature
of the Gaussian curvature  of a 2-dimensional Riemannian manifold
of a 2-dimensional Riemannian manifold 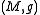 is invariant under changes of the Riemannian metric
is invariant under changes of the Riemannian metric  . This is the Gauss-Bonnet Theorem.
. This is the Gauss-Bonnet Theorem.
Invariant set
A subset S of the domain U of a mapping T is an invariant set under the mapping when Note that the elements of S are not fixed
Note that the elements of S are not fixedFixed point
"Fixed point" has many meanings in science, most of them mathematical.* Fixed point * Fixed-point combinator* Fixed-point arithmetic, a manner of doing arithmetic on computers* Benchmark , fixed points used by geodesists...
, but rather the set S is fixed in the power set of U.
For example, a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is an invariant subset of the plane under a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
about the circle’s center. Further, a conical surface
Conical surface
In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...
is invariant as a set under a homothety of space.
An invariant set of an operation T is also said to be stable under T. For example, the normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s that are so important in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
are those subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s that are stable under the inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s of the ambient group.
Formal statement
The notion of invariance is formalized in three different ways in mathematics: via group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s, presentations, and deformation.
Unchanged under group action
Firstly, if one has a group G acting on a mathematical object (or set of objects) X, then one may ask for which points x are unchanged, "invariant" under the group action, or under an element g of the group.Very frequently one will have a group acting on a set X and ask for what objects in an associated set
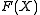 are invariant. For example, rotation in the plane about a point leaves the point that it is rotating about invariant, while translation in the plane does not leave any points invariant, but does leave all lines parallel to the direction of translation invariant as lines. Formally, define the set of lines in the plane P as
are invariant. For example, rotation in the plane about a point leaves the point that it is rotating about invariant, while translation in the plane does not leave any points invariant, but does leave all lines parallel to the direction of translation invariant as lines. Formally, define the set of lines in the plane P as 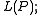 then a rigid motion of the plane takes lines to lines – the group of rigid motions acts on the set of lines – and one may ask which lines are unchanged by an action.
then a rigid motion of the plane takes lines to lines – the group of rigid motions acts on the set of lines – and one may ask which lines are unchanged by an action.More importantly, one may define a function on a set, such as "radius of a circle in the plane" and then ask if this function is invariant under a group action, such as rigid motions.
Dual to the notion of invariants are coinvariants, also known as orbits, which formalizes the notion of congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
: objects which can be taken to each other by a group action. For example, under the group of rigid motions of the plane, the perimeter of a triangle is an invariant, while the set of triangles congruent to a given triangle is a coinvariant.
These are connected as follows: invariants are constant on coinvariants (for example, congruent triangles have the same perimeter), while two objects which agree in the value of one invariant may or may not be congruent (two triangles with the same perimeter need not be congruent). In classification problems, one seeks to find a complete set of invariants
Complete set of invariants
In mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
, such that if two objects have the same values for this set of invariants, they are congruent. For example, triangles such that all three sides are equal are congruent, via SSS congruence, and thus the length of all three sides forms a complete set of invariants for triangles.
Independent of presentation
Secondly, a function may be defined in terms of some presentation or decomposition of a mathematical object; for instance, the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of a cell complex is defined as the alternating sum of the number of cells in each dimension. One may forget the cell complex structure and look only at the underlying topological space (the manifold) – as different cell complexes give the same underlying manifold, one may ask if the function is independent of choice of presentation, in which case it is an intrinsically defined invariant. This is the case for the Euler characteristic, and a general method for defining and computing invariants is to define them for a given presentation and then show that they are independent of the choice of presentation. Note that there is no notion of a group action in this sense.
The most common examples are:
- The presentation of a manifold in terms of coordinate charts – invariants must be unchanged under change of coordinates.
- Various manifold decompositionManifold decompositionIn topology, a branch of mathematics, a manifold M may be decomposed or split by writing M as a combination of smaller pieces. When doing so, one must specify both what those pieces are and how they are put together to form M....
s, as discussed for Euler characteristic. - Invariants of a presentation of a groupPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
.
Unchanged under perturbation
Thirdly, if one is studying an object which varies in a family, as is common in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and differential geometry, one may ask if the property is unchanged under perturbation – if an object is constant on families or invariant under change of metric, for instance.
See also
- Erlangen programErlangen programAn influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
- InvariantInvariant (physics)In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
in physics - Invariant estimatorInvariant estimatorIn statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities...
in statistics - Invariant theoryInvariant theoryInvariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
- Symmetry in mathematicsSymmetry in mathematicsSymmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....
- Topological invariant
- Invariant differential operator
- Invariant measureInvariant measureIn mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
- Invariant subspaceInvariant subspaceIn mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
- Mathematical constantMathematical constantA mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...

