Cokernel
Encyclopedia
In mathematics
, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space
Y/im(f) of the codomain
of f by the image of f.
Cokernels are dual
to the kernels of category theory
, hence the name: the kernel is a subobject of the domain (it maps to the domain), while the cokernel is a quotient object of the codomain (it maps from the codomain).
Intuitively, given an equation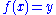
that one is seeking to solve,
the cokernel measures the constraints that y must satisfy for this equation to have a solution – the obstructions to a solution – while the kernel measures the degrees of freedom in a solution, if one exists. This is elaborated in intuition, below.
More generally, the cokernel of a morphism
f : X → Y in some category
(e.g. a homomorphism
between group
s or a bounded linear operator between Hilbert space
s) is an object Q and a morphism q : Y → Q such that the composition q f is the zero morphism
of the category, and furthermore q is universal with respect to this property. Often the map q is understood, and Q itself is called the cokernel of f.
In many situations in abstract algebra
, such as for abelian group
s, vector space
s or module
s, the cokernel of the homomorphism
f : X → Y is the quotient of Y by the image
of f. In topological
settings, such as with bounded linear operators between Hilbert spaces, one typically has to take the closure
of the image before passing to the quotient.
. In order for the definition to make sense the category in question must have zero morphism
s. The cokernel of a morphism
f : X → Y is defined as the coequalizer
of f and the zero morphism 0XY : X → Y.
Explicitly, this means the following. The cokernel of f : X → Y is an object Q together with a morphism q : Y → Q such that the diagram
commutes
. Moreover the morphism q must be universal
for this diagram, i.e. any other such q′: Y → Q′ can be obtained by composing q with a unique morphism u : Q → Q′:
As with all universal constructions the cokernel, if it exists, is unique up to
a unique isomorphism
, or more precisely: if q : Y → Q and q‘ : Y → Q‘ are two cokernels of f : X → Y, then there exists a unique isomorphism u : Q → Q‘ with q‘ = u q.
Like all coequalizers, the cokernel q : Y → Q is necessarily an epimorphism
. Conversely an epimorphism is called normal
(or conormal) if it is the cokernel of some morphism. A category is called conormal if every epimorphism is normal (e.g. the category of groups
is conormal).
, the cokernel of a group homomorphism
f : G → H is the quotient
of H by the normal closure
of the image of f. In the case of abelian group
s, since every subgroup
is normal, the cokernel is just H modulo
the image of f:
, it makes sense to add and subtract morphisms. In such a category, the coequalizer
of two morphisms f and g (if it exists) is just the cokernel of their difference: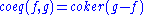
.
In an abelian category
(a special kind of preadditive category) the image
and coimage
of a morphism f are given by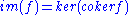
.
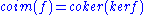In particular, every abelian category is normal (and conormal as well). That is, every monomorphism
m can be written as the kernel of some morphism. Specifically, m is the kernel of its own cokernel: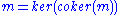
Formally, one may connect the kernel and the cokernel by the exact sequence
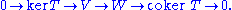
These can be interpreted thus: given a linear equation
to solve,
The dimension of the cokernel plus the dimension of the image (the rank) add up to the dimension of the target space, as the dimension of the quotient space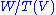
is simply the dimension of the space minus the dimension of the image.
As a simple example, consider the map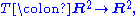
given by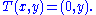 
Then for an equation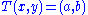
to have a solution, we must have 
(one constraint), and in that case the solution space is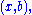 
or equivalently stated, 
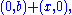(one degree of freedom). The kernel may be expressed as the subspace 
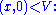the value of x is the freedom in a solution – while the cokernel may be expressed via the map 
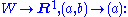given a vector 
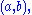the value of a is the obstruction to there being a solution.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
Y/im(f) of the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of f by the image of f.
Cokernels are dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
to the kernels of category theory
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
, hence the name: the kernel is a subobject of the domain (it maps to the domain), while the cokernel is a quotient object of the codomain (it maps from the codomain).
Intuitively, given an equation
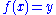that one is seeking to solve,the cokernel measures the constraints that y must satisfy for this equation to have a solution – the obstructions to a solution – while the kernel measures the degrees of freedom in a solution, if one exists. This is elaborated in intuition, below.
More generally, the cokernel of a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : X → Y in some category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
(e.g. a homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
between group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s or a bounded linear operator between Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s) is an object Q and a morphism q : Y → Q such that the composition q f is the zero morphism
Zero morphism
In category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
of the category, and furthermore q is universal with respect to this property. Often the map q is understood, and Q itself is called the cokernel of f.
In many situations in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, such as for abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s or module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s, the cokernel of the homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
f : X → Y is the quotient of Y by the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of f. In topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
settings, such as with bounded linear operators between Hilbert spaces, one typically has to take the closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of the image before passing to the quotient.
Formal definition
One can define the cokernel in the general framework of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. In order for the definition to make sense the category in question must have zero morphism
Zero morphism
In category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
s. The cokernel of a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : X → Y is defined as the coequalizer
Coequalizer
In category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
of f and the zero morphism 0XY : X → Y.
Explicitly, this means the following. The cokernel of f : X → Y is an object Q together with a morphism q : Y → Q such that the diagram
commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
. Moreover the morphism q must be universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
for this diagram, i.e. any other such q′: Y → Q′ can be obtained by composing q with a unique morphism u : Q → Q′:
As with all universal constructions the cokernel, if it exists, is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, or more precisely: if q : Y → Q and q‘ : Y → Q‘ are two cokernels of f : X → Y, then there exists a unique isomorphism u : Q → Q‘ with q‘ = u q.
Like all coequalizers, the cokernel q : Y → Q is necessarily an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
. Conversely an epimorphism is called normal
Normal morphism
In category theory and its applications to mathematics, a normal monomorphism or conormal epimorphism is a particularly well-behaved type of morphism.A normal category is a category in which every monomorphism is normal...
(or conormal) if it is the cokernel of some morphism. A category is called conormal if every epimorphism is normal (e.g. the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
is conormal).
Examples
In the category of groupsCategory of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, the cokernel of a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
f : G → H is the quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of H by the normal closure
Normal closure
The term normal closure is used in two senses in mathematics:* In group theory, the normal closure of a subset of a group is the smallest normal subgroup that contains the subset; see conjugate closure....
of the image of f. In the case of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, since every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
is normal, the cokernel is just H modulo
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
the image of f:
- coker(f) = H / im(f).
Special cases
In a preadditive categoryPreadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
, it makes sense to add and subtract morphisms. In such a category, the coequalizer
Coequalizer
In category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
of two morphisms f and g (if it exists) is just the cokernel of their difference:
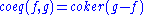.In an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
(a special kind of preadditive category) the image
Image (category theory)
Given a category C and a morphismf\colon X\to Y in C, the image of f is a monomorphism h\colon I\to Y satisfying the following universal property:#There exists a morphism g\colon X\to I such that f = hg....
and coimage
Coimage
In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies....
of a morphism f are given by
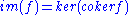
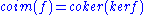.In particular, every abelian category is normal (and conormal as well). That is, every monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
m can be written as the kernel of some morphism. Specifically, m is the kernel of its own cokernel:
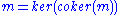
Intuition
The cokernel can be thought of as the space of constraints that an equation must satisfy, as the space of obstructions, just as the kernel is the space of solutions.Formally, one may connect the kernel and the cokernel by the exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
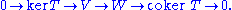
These can be interpreted thus: given a linear equation
to solve,
- the kernel is the space of solutions to the homogeneous equation
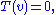and its dimension is the number of degrees of freedom in a solution, if it exists; - the cokernel is the space of constraints that must be satisfied if the equation is to have a solution, and its dimension is the number of constraints that must be satisfied for the equation to have a solution.
The dimension of the cokernel plus the dimension of the image (the rank) add up to the dimension of the target space, as the dimension of the quotient space
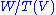is simply the dimension of the space minus the dimension of the image.As a simple example, consider the map
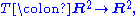given by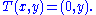 Then for an equation
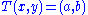to have a solution, we must have (one constraint), and in that case the solution space is 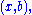or equivalently stated, 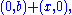(one degree of freedom). The kernel may be expressed as the subspace 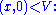the value of x is the freedom in a solution – while the cokernel may be expressed via the map 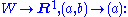given a vector 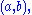the value of a is the obstruction to there being a solution.