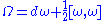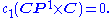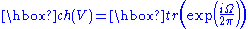Chern class
Encyclopedia
In mathematics
, in particular in algebraic topology
and differential geometry
, the Chern classes are characteristic class
es associated to complex vector bundle
s.
Chern classes were introduced by .
es. They are topological invariants associated to vector bundles on a smooth manifold. The question of whether two ostensibly different vector bundles are the same can be quite hard to answer. The Chern classes provide a simple test: if the Chern classes of a pair of vector bundles do not agree, then the vector bundles are different. The converse, however, is not true.
In topology, differential geometry, and algebraic geometry, it is often important to count how many linearly independent sections a vector bundle has. The Chern classes offer some information about this through, for instance, the Riemann-Roch theorem and the Atiyah-Singer index theorem.
Chern classes are also feasible to calculate in practice. In differential geometry (and some types of algebraic geometry), the Chern classes can be expressed as polynomials in the coefficients of the curvature form
.
V of complex rank
n over a smooth manifold M,
a representative of each Chern class (also called a Chern form)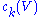 of V are given as the coefficients of the characteristic polynomial
of V are given as the coefficients of the characteristic polynomial
of the curvature form
 of V.
of V.
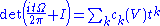
The determinant is over the ring of n×n matrices whose entries are polynomials in t with coefficients in the commutative algebra of even complex differential forms on M. The curvature form
 of V is defined as
of V is defined as
with the connection form
the connection form
and d the exterior derivative
, or via the same expression in which is a gauge form for the gauge group of V. The scalar t is used here only as an indeterminate
is a gauge form for the gauge group of V. The scalar t is used here only as an indeterminate
to generate
the sum from the determinant, and I denotes the n×n identity matrix
.
To say that the expression given is a representative of the Chern class indicates that 'class' here means up to
addition of an exact differential form. That is, Chern classes are cohomology classes in the sense of de Rham cohomology
. It can be shown that the cohomology class of the Chern forms do not depend on the choice of connection in V.
: 1-dimensional complex projective space
. Suppose that z is a holomorphic local coordinate
for the Riemann sphere. Let V = TCP1 be the bundle of complex tangent vectors having the form a∂/∂z at each point, where a is a complex number. We prove the complex version of the hairy ball theorem
: V has no section which is everywhere nonzero.
For this, we need the following fact: the first Chern class of a trivial bundle is zero, i.e.,
This is evinced by the fact that a trivial bundle always admits a flat connection.
So, we shall show that
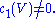
Consider the Kähler metric
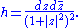
One readily shows that the curvature 2-form is given by

Furthermore, by the definition of the first Chern class
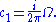
We must show that the cohomology class of this is non-zero. It suffices to compute its integral over the Riemann sphere:
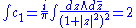
after switching to polar coordinates. By Stokes' theorem
, an exact form would integrate to 0, so the cohomology class is nonzero.
This proves that TCP1 is not a trivial vector bundle.
V over a topological space
X,
the Chern classes of V are a sequence of elements of the cohomology
of X. The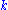 th Chern class of V, which is usually denoted ck(V), is an element of
th Chern class of V, which is usually denoted ck(V), is an element of
the cohomology of X with integer
coefficients. One can also define the total Chern class
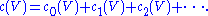
The Chern classes satisfy the following four axioms:
Axiom 1.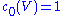 for all
for all 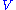 .
.
Axiom 2. Functoriality: If is continuous and
is continuous and 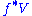 is the vector bundle pullback
is the vector bundle pullback
of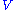 , then
, then 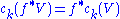 .
.
Axiom 3. Whitney
sum formula: If is another complex vector bundle, then the Chern classes of the direct sum
is another complex vector bundle, then the Chern classes of the direct sum  are given by
are given by
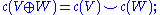
that is,
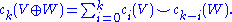
Axiom 4. Normalization: The total Chern class of the tautological line bundle over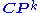 is
is 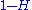 , where
, where  is Poincaré-dual
is Poincaré-dual
to the hyperplane
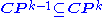 .
.
Alternatively, Alexander Grothendieck
replaced these with a slightly smaller set of axioms:
In fact, these properties uniquely characterize the Chern classes. They imply, among other things:
Since the values are in integral cohomology groups, rather than cohomology with real coefficients, these Chern classes are slightly more refined than those in the Riemannian example.
The original approach to Chern classes was via algebraic topology: the Chern classes arise via homotopy theory which provides a mapping associated to V to a classifying space
(an infinite Grassmannian
in this case). Any vector bundle V over a manifold may be realized as the pullback of a universal bundle over the classifying space, and the Chern classes of V can therefore be defined as the pullback of the Chern classes of the universal bundle; these universal Chern classes in turn can be explicitly written down in terms of Schubert cycles.
Chern's approach used differential geometry, via the curvature approach described predominantly in this article. He showed that the earlier definition was in fact equivalent to his.
There is also an approach of Alexander Grothendieck
showing that axiomatically one need only define the line bundle case.
Chern classes arise naturally in algebraic geometry
. The generalized Chern classes in algebraic geometry can be defined for vector bundles (or more precisely, locally free sheaves) over any nonsingular variety. Algebro-geometric Chern classes do not require the underlying field to have any special properties. In particular, the vector bundles need not necessarily be complex.
Regardless of the particular paradigm, the intuitive meaning of the Chern class concerns 'required zeroes' of a section
of a vector bundle: for example the theorem saying one can't comb a hairy ball flat (hairy ball theorem
). Although that is strictly speaking a question about a real vector bundle (the "hairs" on a ball are actually copies of the real line), there are generalizations in which the hairs are complex (see the example of the complex hairy ball theorem above), or for 1-dimensional projective spaces over many other fields.
See Chern-Simons for more discussion.
. Then the only nontrivial Chern class is the first Chern class, which is an element of the second cohomology group of X. As it is the top Chern class, it equals the Euler class
of the bundle.
The first Chern class turns out to be a complete invariant with which to classify complex line bundles, topologically speaking. That is, there is a bijection
between the isomorphism classes of line bundles over X and the elements of H²(X;Z), which associates to a line bundle its first Chern class. Addition in the second dimensional cohomology group coincides with tensor product
of complex line bundles.
In algebraic geometry, this classification of (isomorphism classes of) complex line bundles by the first Chern class is a crude approximation to the classification of (isomorphism classes of) holomorphic line bundles by linear equivalence classes of divisor
s.
For complex vector bundles of dimension greater than one, the Chern classes are not a complete invariant.
invariants for almost complex manifold
s.
If M is an almost complex manifold, then its tangent bundle
is a complex vector bundle. The Chern classes of M are thus defined to be the Chern classes of its tangent bundle. If M is also compact
and of dimension 2d, then each monomial
of total degree 2d in the Chern classes can be paired with the fundamental class
of M, giving an integer, a Chern number of M.
If M′ is another almost complex manifold of the same dimension, then it is cobordant to M if and only if the Chern numbers of M′ coincide with those of M.
The formal properties of the Chern classes remain the same, with one crucial difference: the rule which computes the first Chern class of a tensor product of line bundles in terms of first Chern classes of the factors is not (ordinary) addition, but rather a formal group law.
The Chern numbers of the tangent bundle of a complex (or almost complex) manifold are called the Chern numbers of the manifold, and are important invariants.
of a space to (the completion of) its rational cohomology. For a line bundle L, the Chern character ch is defined by

More generally, if is a direct sum of line bundles, with first Chern classes
is a direct sum of line bundles, with first Chern classes 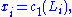 the Chern character is defined additively
the Chern character is defined additively
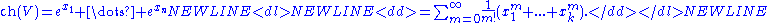
Observe that when V is a sum of line bundles, the Chern classes of V can be expressed as elementary symmetric polynomials in the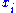 ,
, 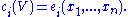
In particular, on the one hand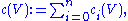
while on the other hand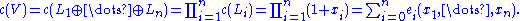
Consequently, Newton's identities may be used to reexpress the power sums in ch(V) above solely in terms of the Chern classes of V, giving
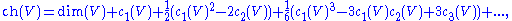
This last expression, justified by invoking the splitting principle
, is taken as the definition ch(V) for arbitrary vector bundles V.
If a connection is used to define the Chern classes, then the explicit form of the Chern character is
where Ω is the curvature of the connection.
The Chern character is useful in part because it facilitates the computation of the Chern class of a tensor product. Specifically, it obeys the following identities: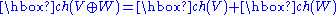
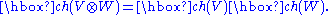
As stated above, using the Grothendieck additivity axiom for Chern classes, the first of these identities can be generalized to state that ch is a homomorphism
of abelian groups from the K-theory
K(X) into the rational cohomology of X. The second identity establishes the fact that this homomorphism also respects products in K(X), and so ch is a homomorphism of rings.
The Chern character is used in the Hirzebruch-Riemann-Roch theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and differential geometry
Differential geometry and topology
Differential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
, the Chern classes are characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es associated to complex vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s.
Chern classes were introduced by .
Basic idea and motivation
Chern classes are characteristic classCharacteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. They are topological invariants associated to vector bundles on a smooth manifold. The question of whether two ostensibly different vector bundles are the same can be quite hard to answer. The Chern classes provide a simple test: if the Chern classes of a pair of vector bundles do not agree, then the vector bundles are different. The converse, however, is not true.
In topology, differential geometry, and algebraic geometry, it is often important to count how many linearly independent sections a vector bundle has. The Chern classes offer some information about this through, for instance, the Riemann-Roch theorem and the Atiyah-Singer index theorem.
Chern classes are also feasible to calculate in practice. In differential geometry (and some types of algebraic geometry), the Chern classes can be expressed as polynomials in the coefficients of the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
.
The Chern class of a Hermitian vector bundle on a smooth manifold
Given a complex hermitian vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
V of complex rank
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
n over a smooth manifold M,
a representative of each Chern class (also called a Chern form)
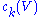 of V are given as the coefficients of the characteristic polynomial
of V are given as the coefficients of the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
 of V.
of V.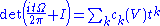
The determinant is over the ring of n×n matrices whose entries are polynomials in t with coefficients in the commutative algebra of even complex differential forms on M. The curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
 of V is defined as
of V is defined aswith
 the connection form
the connection formConnection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
and d the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, or via the same expression in which
 is a gauge form for the gauge group of V. The scalar t is used here only as an indeterminate
is a gauge form for the gauge group of V. The scalar t is used here only as an indeterminateIndeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
to generate
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
the sum from the determinant, and I denotes the n×n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
To say that the expression given is a representative of the Chern class indicates that 'class' here means up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
addition of an exact differential form. That is, Chern classes are cohomology classes in the sense of de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. It can be shown that the cohomology class of the Chern forms do not depend on the choice of connection in V.
Example: the complex tangent bundle of the Riemann sphere
Let CP1 be the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
: 1-dimensional complex projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Suppose that z is a holomorphic local coordinate
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
for the Riemann sphere. Let V = TCP1 be the bundle of complex tangent vectors having the form a∂/∂z at each point, where a is a complex number. We prove the complex version of the hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
: V has no section which is everywhere nonzero.
For this, we need the following fact: the first Chern class of a trivial bundle is zero, i.e.,
This is evinced by the fact that a trivial bundle always admits a flat connection.
So, we shall show that
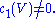
Consider the Kähler metric
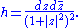
One readily shows that the curvature 2-form is given by

Furthermore, by the definition of the first Chern class
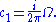
We must show that the cohomology class of this is non-zero. It suffices to compute its integral over the Riemann sphere:
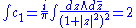
after switching to polar coordinates. By Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, an exact form would integrate to 0, so the cohomology class is nonzero.
This proves that TCP1 is not a trivial vector bundle.
Properties of Chern classes
Given a complex vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
V over a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X,
the Chern classes of V are a sequence of elements of the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of X. The
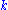 th Chern class of V, which is usually denoted ck(V), is an element of
th Chern class of V, which is usually denoted ck(V), is an element of- H2k(X;Z),
the cohomology of X with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients. One can also define the total Chern class
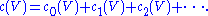
The Chern classes satisfy the following four axioms:
Axiom 1.
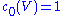 for all
for all 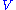 .
.Axiom 2. Functoriality: If
 is continuous and
is continuous and 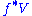 is the vector bundle pullback
is the vector bundle pullbackPullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of
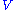 , then
, then 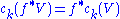 .
.Axiom 3. Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
sum formula: If
 is another complex vector bundle, then the Chern classes of the direct sum
is another complex vector bundle, then the Chern classes of the direct sum  are given by
are given by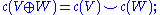
that is,
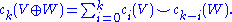
Axiom 4. Normalization: The total Chern class of the tautological line bundle over
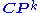 is
is 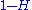 , where
, where  is Poincaré-dual
is Poincaré-dualPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
to the hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
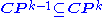 .
.Alternatively, Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
replaced these with a slightly smaller set of axioms:
- Functoriality: (Same as above)
- Additivity: If
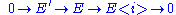 is an exact sequenceExact sequenceAn exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
is an exact sequenceExact sequenceAn exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of vector bundles, then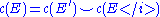 .
.
- Normalization: If E is a line bundleLine bundleIn mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
, then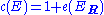 where
where 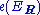 is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the underlying real vector bundle.
In fact, these properties uniquely characterize the Chern classes. They imply, among other things:
- If
 is the complex rank of
is the complex rank of  , then
, then 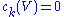 for all
for all  . Thus the total Chern class terminates.
. Thus the total Chern class terminates.
- The top Chern class of
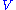 (meaning
(meaning  , where
, where  is the rank of
is the rank of  ) is always equal to the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
) is always equal to the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the underlying real vector bundle.
Since the values are in integral cohomology groups, rather than cohomology with real coefficients, these Chern classes are slightly more refined than those in the Riemannian example.
Construction of Chern classes
There are various ways of approaching the subject, each of which focuses on a slightly different flavor of Chern class.The original approach to Chern classes was via algebraic topology: the Chern classes arise via homotopy theory which provides a mapping associated to V to a classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
(an infinite Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
in this case). Any vector bundle V over a manifold may be realized as the pullback of a universal bundle over the classifying space, and the Chern classes of V can therefore be defined as the pullback of the Chern classes of the universal bundle; these universal Chern classes in turn can be explicitly written down in terms of Schubert cycles.
Chern's approach used differential geometry, via the curvature approach described predominantly in this article. He showed that the earlier definition was in fact equivalent to his.
There is also an approach of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
showing that axiomatically one need only define the line bundle case.
Chern classes arise naturally in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The generalized Chern classes in algebraic geometry can be defined for vector bundles (or more precisely, locally free sheaves) over any nonsingular variety. Algebro-geometric Chern classes do not require the underlying field to have any special properties. In particular, the vector bundles need not necessarily be complex.
Regardless of the particular paradigm, the intuitive meaning of the Chern class concerns 'required zeroes' of a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of a vector bundle: for example the theorem saying one can't comb a hairy ball flat (hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
). Although that is strictly speaking a question about a real vector bundle (the "hairs" on a ball are actually copies of the real line), there are generalizations in which the hairs are complex (see the example of the complex hairy ball theorem above), or for 1-dimensional projective spaces over many other fields.
See Chern-Simons for more discussion.
Chern classes of line bundles
An important special case occurs when V is a line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
. Then the only nontrivial Chern class is the first Chern class, which is an element of the second cohomology group of X. As it is the top Chern class, it equals the Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the bundle.
The first Chern class turns out to be a complete invariant with which to classify complex line bundles, topologically speaking. That is, there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the isomorphism classes of line bundles over X and the elements of H²(X;Z), which associates to a line bundle its first Chern class. Addition in the second dimensional cohomology group coincides with tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of complex line bundles.
In algebraic geometry, this classification of (isomorphism classes of) complex line bundles by the first Chern class is a crude approximation to the classification of (isomorphism classes of) holomorphic line bundles by linear equivalence classes of divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s.
For complex vector bundles of dimension greater than one, the Chern classes are not a complete invariant.
Chern classes of almost complex manifolds and cobordism
The theory of Chern classes gives rise to cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
invariants for almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
s.
If M is an almost complex manifold, then its tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
is a complex vector bundle. The Chern classes of M are thus defined to be the Chern classes of its tangent bundle. If M is also compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and of dimension 2d, then each monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
of total degree 2d in the Chern classes can be paired with the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
of M, giving an integer, a Chern number of M.
If M′ is another almost complex manifold of the same dimension, then it is cobordant to M if and only if the Chern numbers of M′ coincide with those of M.
Generalizations
There is a generalization of the theory of Chern classes, where ordinary cohomology is replaced with a generalized cohomology theory. The theories for which such generalization is possible are called complex orientable.The formal properties of the Chern classes remain the same, with one crucial difference: the rule which computes the first Chern class of a tensor product of line bundles in terms of first Chern classes of the factors is not (ordinary) addition, but rather a formal group law.
Chern numbers
If we work on an oriented manifold of dimension 2n, then any product of Chern classes of total degree 2n can be paired with the orientation homology class (or "integrated over the manifold") to give an integer, a Chern number of the vector bundle. For example, if the manifold has dimension 6, there are three linearly independent Chern numbers, given by c1³, c1c2, and c3. In general, if the manifold has dimension 2n, the number of possible independent Chern numbers is the number of partitions of n.The Chern numbers of the tangent bundle of a complex (or almost complex) manifold are called the Chern numbers of the manifold, and are important invariants.
The Chern character
Chern classes can be used to construct a homomorphism of rings from the topological K-theoryTopological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
of a space to (the completion of) its rational cohomology. For a line bundle L, the Chern character ch is defined by

More generally, if
 is a direct sum of line bundles, with first Chern classes
is a direct sum of line bundles, with first Chern classes 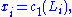 the Chern character is defined additively
the Chern character is defined additively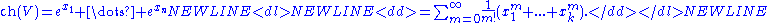
Observe that when V is a sum of line bundles, the Chern classes of V can be expressed as elementary symmetric polynomials in the
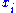 ,
, 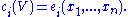
In particular, on the one hand
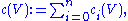
while on the other hand
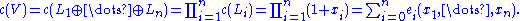
Consequently, Newton's identities may be used to reexpress the power sums in ch(V) above solely in terms of the Chern classes of V, giving
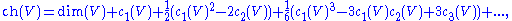
This last expression, justified by invoking the splitting principle
Splitting principle
In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
, is taken as the definition ch(V) for arbitrary vector bundles V.
If a connection is used to define the Chern classes, then the explicit form of the Chern character is
where Ω is the curvature of the connection.
The Chern character is useful in part because it facilitates the computation of the Chern class of a tensor product. Specifically, it obeys the following identities:
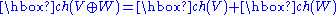
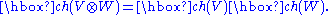
As stated above, using the Grothendieck additivity axiom for Chern classes, the first of these identities can be generalized to state that ch is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of abelian groups from the K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
K(X) into the rational cohomology of X. The second identity establishes the fact that this homomorphism also respects products in K(X), and so ch is a homomorphism of rings.
The Chern character is used in the Hirzebruch-Riemann-Roch theorem
Hirzebruch-Riemann-Roch theorem
In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions...
.
External links
- Vector Bundles & K-Theory - A downloadable book-in-progress by Allen HatcherAllen HatcherAllen Edward Hatcher is an American topologist and also a noted author. His book Algebraic Topology, which is the first in a series, is considered by many to be one of the best introductions to the subject....
. Contains a chapter about characteristic classes. - Dieter Kotschick, Chern numbers of algebraic varieties