
Quantum cohomology
Encyclopedia
In mathematics
, specifically in symplectic topology
and algebraic geometry
, a quantum cohomology ring
is an extension of the ordinary cohomology
ring of a closed
symplectic manifold
. It comes in two versions, called small and big; in general, the latter is more complicated and contains more information than the former. In each, the choice of coefficient ring (typically a Novikov ring, described below) significantly affects its structure, as well.
While the cup product
of ordinary cohomology describes how subspaces of the manifold intersect
each other, the quantum cup product of quantum cohomology describes how subspaces intersect in a "fuzzy", "quantum" way. More precisely, they intersect if they are connected via one or more pseudoholomorphic curve
s. Gromov-Witten invariant
s, which count these curves, appear as coefficients in expansions of the quantum cup product.
Because it expresses a structure or pattern for Gromov-Witten invariants, quantum cohomology has important implications for enumerative geometry
. It also connects to many ideas in mathematical physics
and mirror symmetry
. In particular, it is ring-isomorphic
to Floer homology
.
Throughout this article, X is a closed symplectic manifold with symplectic form .
.
of X. This allows the quantum cup product, defined below, to record information about pseudoholomorphic curves in X. For example, let

be the second homology modulo
its torsion
. Let R be any commutative ring with unit and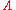 the ring of formal power series of the form
the ring of formal power series of the form

where
The variable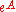 is considered to be of degree
is considered to be of degree 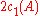 , where
, where 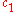 is the first Chern class
is the first Chern class
of the tangent bundle
 , regarded as a complex
, regarded as a complex
vector bundle
by choosing any almost complex structure
compatible with . Thus
. Thus 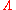 is a graded ring, called the Novikov ring for
is a graded ring, called the Novikov ring for  . (Alternative definitions are common.)
. (Alternative definitions are common.)
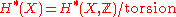
be the cohomology of X modulo torsion. Define the small quantum cohomology with coefficients in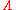 to be
to be
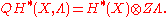
Its elements are finite sums of the form
The small quantum cohomology is a graded R-module with
The ordinary cohomology embeds into
embeds into  via
via  , and
, and  is generated as a
is generated as a  -module by
-module by 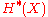 .
.
For any two cohomology classes in
in 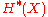 of pure degree, and for any A in
of pure degree, and for any A in 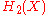 , define
, define 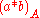 to be the unique element of
to be the unique element of 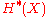 such that
such that
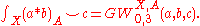
(The right-hand side is a genus- ,
,  -point Gromov-Witten invariant.) Then define
-point Gromov-Witten invariant.) Then define
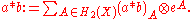
This extends by linearity to a well-defined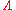 -bilinear map
-bilinear map
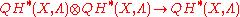
called the small quantum cup product.
 are constant maps, whose images are points. It follows that
are constant maps, whose images are points. It follows that
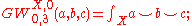
in other words,

Thus the quantum cup product contains the ordinary cup product; it extends the ordinary cup product to nonzero classes A.
In general, the Poincaré dual of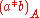 corresponds to the space of pseudoholomorphic curves of class A passing through the Poincaré duals of a and b. So while the ordinary cohomology considers a and b to intersect only when they meet at one or more points, the quantum cohomology records a nonzero intersection for a and b whenever they are connected by one or more pseudoholomorphic curves. The Novikov ring just provides a bookkeeping system large enough to record this intersection information for all classes A.
corresponds to the space of pseudoholomorphic curves of class A passing through the Poincaré duals of a and b. So while the ordinary cohomology considers a and b to intersect only when they meet at one or more points, the quantum cohomology records a nonzero intersection for a and b whenever they are connected by one or more pseudoholomorphic curves. The Novikov ring just provides a bookkeeping system large enough to record this intersection information for all classes A.
with its standard symplectic form (corresponding to the Fubini-Study metric
) and complex structure. Let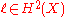 be the Poincaré dual of a line L. Then
be the Poincaré dual of a line L. Then
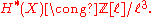
The only nonzero Gromov-Witten invariants are those of class or
or  . It turns out that
. It turns out that
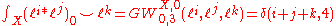
and
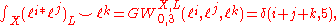
where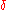 is the Kronecker delta. Therefore
is the Kronecker delta. Therefore


In this case it is convenient to rename as q and use the simpler coefficient ring
as q and use the simpler coefficient ring 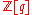 . This q is of degree
. This q is of degree  . Then
. Then

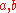 of pure degree,
of pure degree,
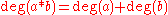
and

The small quantum cup product is distributive
and -bilinear. The identity element
-bilinear. The identity element
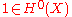 is also the identity element for small quantum cohomology.
is also the identity element for small quantum cohomology.
The small quantum cup product is also associative
. This is a consequence of the gluing law for Gromov-Witten invariants, a difficult technical result. It is tantamount to the fact that the Gromov-Witten potential
(a generating function
for the genus- Gromov-Witten invariants) satisfies a certain third-order differential equation
Gromov-Witten invariants) satisfies a certain third-order differential equation
known as the WDVV equation.
An intersection pairing
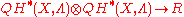
is defined by
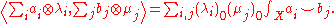
(The subscripts indicate the
indicate the  coefficient.) This pairing satisfies the associativity property
coefficient.) This pairing satisfies the associativity property

 , one can view the evenly-graded part H of the vector space
, one can view the evenly-graded part H of the vector space 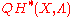 as a complex manifold. The small quantum cup product restricts to a well-defined, commutative product on H. Under mild assumptions, H with the intersection pairing
as a complex manifold. The small quantum cup product restricts to a well-defined, commutative product on H. Under mild assumptions, H with the intersection pairing  is then a Frobenius algebra
is then a Frobenius algebra
.
The quantum cup product can be viewed as a connection
on the tangent bundle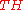 , called the Dubrovin connection. Commutativity and associativity of the quantum cup product then correspond to zero-torsion and zero-curvature
, called the Dubrovin connection. Commutativity and associativity of the quantum cup product then correspond to zero-torsion and zero-curvature
conditions on this connection.
 such that
such that  and the Dubrovin connection give U the structure of a Frobenius manifold
and the Dubrovin connection give U the structure of a Frobenius manifold
. Any a in U defines a quantum cup product
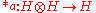
by the formula

Collectively, these products on H are called the big quantum cohomology. All of the genus- Gromov-Witten invariants are recoverable from it; in general, the same is not true of the simpler small quantum cohomology.
Gromov-Witten invariants are recoverable from it; in general, the same is not true of the simpler small quantum cohomology.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a quantum cohomology ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is an extension of the ordinary cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
ring of a closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. It comes in two versions, called small and big; in general, the latter is more complicated and contains more information than the former. In each, the choice of coefficient ring (typically a Novikov ring, described below) significantly affects its structure, as well.
While the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
of ordinary cohomology describes how subspaces of the manifold intersect
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
each other, the quantum cup product of quantum cohomology describes how subspaces intersect in a "fuzzy", "quantum" way. More precisely, they intersect if they are connected via one or more pseudoholomorphic curve
Pseudoholomorphic curve
In mathematics, specifically in topology and geometry, a pseudoholomorphic curve is a smooth map from a Riemann surface into an almost complex manifold that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of...
s. Gromov-Witten invariant
Gromov-Witten invariant
In mathematics, specifically in symplectic topology and algebraic geometry, Gromov–Witten invariants are rational numbers that, in certain situations, count pseudoholomorphic curves meeting prescribed conditions in a given symplectic manifold...
s, which count these curves, appear as coefficients in expansions of the quantum cup product.
Because it expresses a structure or pattern for Gromov-Witten invariants, quantum cohomology has important implications for enumerative geometry
Enumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...
. It also connects to many ideas in mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
and mirror symmetry
Mirror symmetry
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden...
. In particular, it is ring-isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
.
Throughout this article, X is a closed symplectic manifold with symplectic form
 .
.Novikov ring
Various choices of coefficient ring for the quantum cohomology of X are possible. Usually a ring is chosen that encodes information about the second homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of X. This allows the quantum cup product, defined below, to record information about pseudoholomorphic curves in X. For example, let

be the second homology modulo
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
its torsion
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
. Let R be any commutative ring with unit and
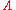 the ring of formal power series of the form
the ring of formal power series of the form
where
- the coefficients
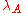 come from R,
come from R, - the
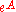 are formal variables subject to the relation
are formal variables subject to the relation  ,
, - for every real number C, only finitely many A with
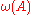 less than or equal to C have nonzero coefficients
less than or equal to C have nonzero coefficients 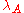 .
.
The variable
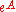 is considered to be of degree
is considered to be of degree 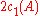 , where
, where 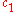 is the first Chern class
is the first Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
 , regarded as a complex
, regarded as a complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
by choosing any almost complex structure
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
compatible with
 . Thus
. Thus 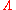 is a graded ring, called the Novikov ring for
is a graded ring, called the Novikov ring for  . (Alternative definitions are common.)
. (Alternative definitions are common.)Small quantum cohomology
Let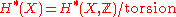
be the cohomology of X modulo torsion. Define the small quantum cohomology with coefficients in
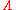 to be
to be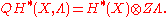
Its elements are finite sums of the form
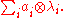
The small quantum cohomology is a graded R-module with
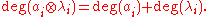
The ordinary cohomology
 embeds into
embeds into  via
via  , and
, and 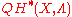 is generated as a
is generated as a 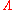 -module by
-module by 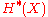 .
.For any two cohomology classes
 in
in 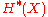 of pure degree, and for any A in
of pure degree, and for any A in 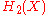 , define
, define 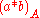 to be the unique element of
to be the unique element of 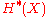 such that
such that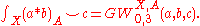
(The right-hand side is a genus-
 ,
,  -point Gromov-Witten invariant.) Then define
-point Gromov-Witten invariant.) Then define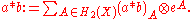
This extends by linearity to a well-defined
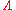 -bilinear map
-bilinear map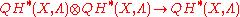
called the small quantum cup product.
Geometric interpretation
The only pseudoholomorphic curves in class are constant maps, whose images are points. It follows that
are constant maps, whose images are points. It follows that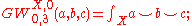
in other words,

Thus the quantum cup product contains the ordinary cup product; it extends the ordinary cup product to nonzero classes A.
In general, the Poincaré dual of
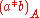 corresponds to the space of pseudoholomorphic curves of class A passing through the Poincaré duals of a and b. So while the ordinary cohomology considers a and b to intersect only when they meet at one or more points, the quantum cohomology records a nonzero intersection for a and b whenever they are connected by one or more pseudoholomorphic curves. The Novikov ring just provides a bookkeeping system large enough to record this intersection information for all classes A.
corresponds to the space of pseudoholomorphic curves of class A passing through the Poincaré duals of a and b. So while the ordinary cohomology considers a and b to intersect only when they meet at one or more points, the quantum cohomology records a nonzero intersection for a and b whenever they are connected by one or more pseudoholomorphic curves. The Novikov ring just provides a bookkeeping system large enough to record this intersection information for all classes A.Example
Let X be the complex projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
with its standard symplectic form (corresponding to the Fubini-Study metric
Fubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
) and complex structure. Let
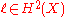 be the Poincaré dual of a line L. Then
be the Poincaré dual of a line L. Then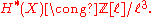
The only nonzero Gromov-Witten invariants are those of class
 or
or  . It turns out that
. It turns out that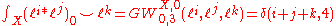
and
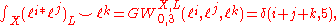
where
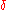 is the Kronecker delta. Therefore
is the Kronecker delta. Therefore

In this case it is convenient to rename
 as q and use the simpler coefficient ring
as q and use the simpler coefficient ring 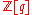 . This q is of degree
. This q is of degree  . Then
. Then
Properties of the small quantum cup product
For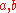 of pure degree,
of pure degree,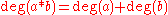
and

The small quantum cup product is distributive
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
and
 -bilinear. The identity element
-bilinear. The identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
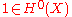 is also the identity element for small quantum cohomology.
is also the identity element for small quantum cohomology.The small quantum cup product is also associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
. This is a consequence of the gluing law for Gromov-Witten invariants, a difficult technical result. It is tantamount to the fact that the Gromov-Witten potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
(a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the genus-
 Gromov-Witten invariants) satisfies a certain third-order differential equation
Gromov-Witten invariants) satisfies a certain third-order differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
known as the WDVV equation.
An intersection pairing
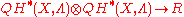
is defined by
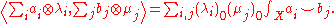
(The subscripts
 indicate the
indicate the  coefficient.) This pairing satisfies the associativity property
coefficient.) This pairing satisfies the associativity property
Dubrovin connection
When the base ring R is , one can view the evenly-graded part H of the vector space
, one can view the evenly-graded part H of the vector space 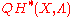 as a complex manifold. The small quantum cup product restricts to a well-defined, commutative product on H. Under mild assumptions, H with the intersection pairing
as a complex manifold. The small quantum cup product restricts to a well-defined, commutative product on H. Under mild assumptions, H with the intersection pairing  is then a Frobenius algebra
is then a Frobenius algebraFrobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
.
The quantum cup product can be viewed as a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on the tangent bundle
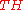 , called the Dubrovin connection. Commutativity and associativity of the quantum cup product then correspond to zero-torsion and zero-curvature
, called the Dubrovin connection. Commutativity and associativity of the quantum cup product then correspond to zero-torsion and zero-curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
conditions on this connection.
Big quantum cohomology
There exists a neighborhood U of such that
such that  and the Dubrovin connection give U the structure of a Frobenius manifold
and the Dubrovin connection give U the structure of a Frobenius manifoldFrobenius manifold
In the mathematical field of differential geometry, a Frobenius manifold is a flat Riemannian manifold with a certain compatible multiplicative structure on the tangent space. The concept generalizes the notion of Frobenius algebra to tangent bundles...
. Any a in U defines a quantum cup product
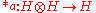
by the formula

Collectively, these products on H are called the big quantum cohomology. All of the genus-
 Gromov-Witten invariants are recoverable from it; in general, the same is not true of the simpler small quantum cohomology.
Gromov-Witten invariants are recoverable from it; in general, the same is not true of the simpler small quantum cohomology.

