
Helmholtz free energy
Encyclopedia
In thermodynamics
, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed
thermodynamic system
at a constant temperature and volume. For such a system, the negative of the difference in the Helmholtz energy is equal to the maximum amount of work extractable from a thermodynamic process in which temperature and volume are held constant. Under these conditions, it is minimized at equilibrium. The Helmholtz free energy was developed by Hermann von Helmholtz
and is usually denoted by the letter A (from the German “Arbeit” or work), or the letter F . The IUPAC recommends the letter A as well as the use of name Helmholtz energy. In physics
, the letter F is usually used to denote the Helmholtz energy, which is often referred to as the Helmholtz function or simply “free energy."
While Gibbs free energy
is most commonly used as a measure of thermodynamic potential, especially in the field of chemistry
, the isobaric
restriction on that quantity is inconvenient for some applications. For example, in explosives research, Helmholtz free energy is often used since explosive reactions by their nature induce pressure changes. It is also frequently used to define fundamental equations of state
in accurate correlations of thermodynamic properties of pure substances.

where
The Helmholtz energy is the negative Legendre transform with respect to the entropy, S, of the fundamental relation in the energy representation, U(S, V, N). The natural variables of A are T, V, N.
we have
 ,
,
where is the internal energy,
is the internal energy,  is the energy added by heating and
is the energy added by heating and 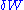 is the work done by the system. From the second law of thermodynamics
is the work done by the system. From the second law of thermodynamics
, for a reversible process
we may say that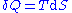 . Also, in case of a reversible change, the work done can be expressed as
. Also, in case of a reversible change, the work done can be expressed as 

Applying the product rule for differentiation to d(TS) = TdS + SdT, we have:
 ,
,
and:
The definition of A = U - TS enables to rewrite this as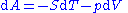
This relation is also valid for a process that is not reversible because A is a thermodynamic function of state.
Since the thermodynamical variables of the system are well defined in the initial state and the final state, the internal energy increase, , the entropy
, the entropy
increase , and the work performed by the system,
, and the work performed by the system,  , are well-defined quantities. Conservation of energy implies:
, are well-defined quantities. Conservation of energy implies:

The volume of the system is kept constant. This means that the volume of the heat bath does not change either and we can conclude that the heat bath does not perform any work. This implies that the amount of heat that flows into the heat bath is given by:

The heat bath remains in thermal equilibrium at temperature T no matter what the system does. Therefore the entropy change of the heat bath is:
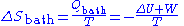
The total entropy change is thus given by:

Since the system is in thermal equilibrium with the heat bath in the initial and the final states, T is also the temperature of the system in these states. The fact that the system's temperature does not change allows us to express the numerator as the free energy change of the system:

Since the total change in entropy must always be larger or equal to zero, we obtain the inequality:

If no work is extracted from the system then
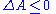
We see that for a system kept at constant temperature and volume, the total free energy during a spontaneous change can only decrease, that the total amount of work that can be extracted is limited by the free energy decrease, and that increasing the free energy requires work to be done on the system.
This result seems to contradict the equation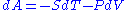 , as keeping T and V constant seems to imply
, as keeping T and V constant seems to imply  and hence
and hence  . In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that
. In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that 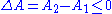 where the
where the  are different thermodynamic functions of state.
are different thermodynamic functions of state.
One can imagine that the spontaneous change is carried out in a sequence of infinitesimally small steps. To describe such a system thermodynamically, one needs to enlarge the thermodynamical state space of the system. In case of a chemical reaction, one must specify the number of particles of each type. The differential of the free energy then generalizes to:

where the are the numbers of particles of type j and the
are the numbers of particles of type j and the  are the corresponding chemical potential
are the corresponding chemical potential
s. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.
In case there are other external parameters the above equation generalizes to:

Here the are the external variables and the
are the external variables and the  the corresponding generalized forces.
the corresponding generalized forces.
. The probability to find the system in some energy eigenstate r is given by:

where



Z is called the partition function
of the system. The fact that the system does not have a unique energy means that the various thermodynamical quantities must be defined as expectation values. In the thermodynamical limit of infinite system size, the relative fluctuations in these averages will go to zero.
The average internal energy of the system is the expectation value of the energy and can be expressed in terms of Z as follows:
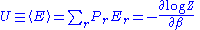
If the system is in state r, then the generalized force corresponding to an external variable x is given by

The thermal average of this can be written as:
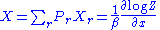
Suppose the system has one external variable x. Then changing the system's temperature parameter by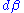 and the external variable by dx will lead to a change in
and the external variable by dx will lead to a change in  :
:
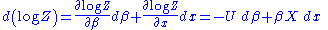
If we write as:
as:

we get:
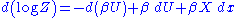
This means that the change in the internal energy is given by:
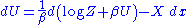
In the thermodynamic limit, the fundamental thermodynamic relation should hold:

This then implies that the entropy of the system is given by:

where c is some constant. The value of c can be determined by considering the limit T → 0. In this limit the entropy becomes where
where  is the ground state degeneracy. The partition function in this limit is
is the ground state degeneracy. The partition function in this limit is  where
where 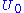 is the ground state energy. Thus, we see that
is the ground state energy. Thus, we see that  and that:
and that:
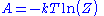
, which is a variational method based on the Bogoliubov inequality. This inequality can be formulated as follows.
Suppose we replace the real Hamiltonian of the model by a trial Hamiltonian
of the model by a trial Hamiltonian  , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
, which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
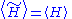
where both averages are taken with respect to the canonical distribution defined by the trial Hamiltonian , then
, then

where is the free energy of the original Hamiltonian and
is the free energy of the original Hamiltonian and 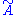 is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
The Bogoliubov inequality is often formulated in a sightly different but equivalent way. If we write the Hamiltonian as:
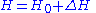
where is exactly solvable, then we can apply the above inequality by defining
is exactly solvable, then we can apply the above inequality by defining

Here we have defined to be the average of X over the canonical ensemble defined by
to be the average of X over the canonical ensemble defined by  . Since
. Since  defined this way differs from
defined this way differs from 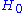 by a constant, we have in general
by a constant, we have in general

Therefore

And thus the inequality
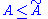
holds. The free energy is the free energy of the model defined by
is the free energy of the model defined by 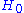 plus
plus  . This means that
. This means that
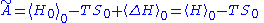
and thus:

 and
and  , respectively. The inequality:
, respectively. The inequality:

then holds. To see this, consider the difference between the left hand side and the right hand side. We can write this as:

Since
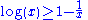
it follows that:

where in the last step we have used that both probability distributions are normalized to 1.
We can write the inequality as:

where the averages are taken with respect to . If we now substitute in here the expressions for the probability distributions:
. If we now substitute in here the expressions for the probability distributions:

and

we get:
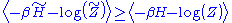
Since the averages of and
and  are, by assumption, identical we have:
are, by assumption, identical we have:

Here we have used that the partition functions are constants with respect to taking averages and that the free energy is proportional to minus the logarithm of the partition function.
We can easily generalize this proof to the case of quantum mechanical models. We denote the eigenstates of by
by 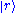 . We denote the diagonal components of the density matrices for the canonical distributions for
. We denote the diagonal components of the density matrices for the canonical distributions for  and
and  in this basis as:
in this basis as:

and

where the are the eigenvalues of
are the eigenvalues of 
We assume again that the averages of H and in the canonical ensemble defined by
in the canonical ensemble defined by 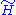 are the same:
are the same:

where
The inequality
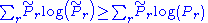
still holds as both the and the
and the  sum to 1. On the l.h.s. we can replace:
sum to 1. On the l.h.s. we can replace:

On the right hand side we can use the inequality

where we have introduced the notation

for the expectation value of the operator Y in the state r. See here for a proof. Taking the logarithm of this inequality gives:

This allows us to write:
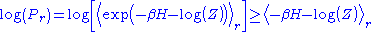
The fact that the averages of H and are the same then leads to the same conclusion as in the classical case:
are the same then leads to the same conclusion as in the classical case:
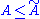
 ) must be replaced by the product of the volume times the stress
) must be replaced by the product of the volume times the stress
times an infinitesimal strain:

where is the stress tensor, and
is the stress tensor, and  is the strain tensor. In the case of linear elastic
is the strain tensor. In the case of linear elastic
materials that obey Hooke's Law
, the stress is related to the strain by:

where we are now using Einstein notation
for the tensors, in which repeated indices in a product are summed. We may integrate the expression for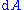 to obtain the Helmholtz energy:
to obtain the Helmholtz energy:


, as given by the IAPWS
in their IAPWS-95 release.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed
Closed system
-In physics:In thermodynamics, a closed system can exchange energy , but not matter, with its surroundings.In contrast, an isolated system cannot exchange any of heat, work, or matter with the surroundings, while an open system can exchange all of heat, work and matter.For a simple system, with...
thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
at a constant temperature and volume. For such a system, the negative of the difference in the Helmholtz energy is equal to the maximum amount of work extractable from a thermodynamic process in which temperature and volume are held constant. Under these conditions, it is minimized at equilibrium. The Helmholtz free energy was developed by Hermann von Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
and is usually denoted by the letter A (from the German “Arbeit” or work), or the letter F . The IUPAC recommends the letter A as well as the use of name Helmholtz energy. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the letter F is usually used to denote the Helmholtz energy, which is often referred to as the Helmholtz function or simply “free energy."
While Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
is most commonly used as a measure of thermodynamic potential, especially in the field of chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, the isobaric
Isobaric
Isobaric may refer to:*in thermodynamics, an isobaric process, i.e. one that is carried out at constant pressure;...
restriction on that quantity is inconvenient for some applications. For example, in explosives research, Helmholtz free energy is often used since explosive reactions by their nature induce pressure changes. It is also frequently used to define fundamental equations of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
in accurate correlations of thermodynamic properties of pure substances.
Definition
The Helmholtz energy is defined as:
where
- A is the Helmholtz free energy (SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
: jouleJouleThe joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s, CGS: ergErgAn erg is the unit of energy and mechanical work in the centimetre-gram-second system of units, symbol "erg". Its name is derived from the Greek ergon, meaning "work"....
s), - U is the internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system (SI: joules, CGS: ergs), - T is the absolute temperature (kelvinKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s), - S is the entropy (SI: joules per kelvin, CGS: ergs per kelvin).
The Helmholtz energy is the negative Legendre transform with respect to the entropy, S, of the fundamental relation in the energy representation, U(S, V, N). The natural variables of A are T, V, N.
Mathematical development
From the first law of thermodynamicsFirst law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
we have
 ,
,where
 is the internal energy,
is the internal energy,  is the energy added by heating and
is the energy added by heating and 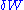 is the work done by the system. From the second law of thermodynamics
is the work done by the system. From the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, for a reversible process
Reversible process (thermodynamics)
In thermodynamics, a reversible process, or reversible cycle if the process is cyclic, is a process that can be "reversed" by means of infinitesimal changes in some property of the system without loss or dissipation of energy. Due to these infinitesimal changes, the system is in thermodynamic...
we may say that
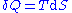 . Also, in case of a reversible change, the work done can be expressed as
. Also, in case of a reversible change, the work done can be expressed as 

Applying the product rule for differentiation to d(TS) = TdS + SdT, we have:
 ,
,and:

The definition of A = U - TS enables to rewrite this as
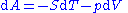
This relation is also valid for a process that is not reversible because A is a thermodynamic function of state.
Minimum free energy and maximum work principles
The laws of thermodynamics are only directly applicable to systems in thermal equilibrium. If we wish to describe phenomena like chemical reactions, then the best we can do is to consider suitably chosen initial and final states in which the system is in (metastable) thermal equilibrium. If the system is kept at fixed volume and is in contact with a heat bath at some constant temperature, then we can reason as follows.Since the thermodynamical variables of the system are well defined in the initial state and the final state, the internal energy increase,
 , the entropy
, the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
increase
 , and the work performed by the system,
, and the work performed by the system,  , are well-defined quantities. Conservation of energy implies:
, are well-defined quantities. Conservation of energy implies:
The volume of the system is kept constant. This means that the volume of the heat bath does not change either and we can conclude that the heat bath does not perform any work. This implies that the amount of heat that flows into the heat bath is given by:

The heat bath remains in thermal equilibrium at temperature T no matter what the system does. Therefore the entropy change of the heat bath is:
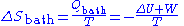
The total entropy change is thus given by:

Since the system is in thermal equilibrium with the heat bath in the initial and the final states, T is also the temperature of the system in these states. The fact that the system's temperature does not change allows us to express the numerator as the free energy change of the system:

Since the total change in entropy must always be larger or equal to zero, we obtain the inequality:

If no work is extracted from the system then
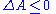
We see that for a system kept at constant temperature and volume, the total free energy during a spontaneous change can only decrease, that the total amount of work that can be extracted is limited by the free energy decrease, and that increasing the free energy requires work to be done on the system.
This result seems to contradict the equation
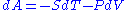 , as keeping T and V constant seems to imply
, as keeping T and V constant seems to imply  and hence
and hence  . In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that
. In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that 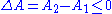 where the
where the  are different thermodynamic functions of state.
are different thermodynamic functions of state.One can imagine that the spontaneous change is carried out in a sequence of infinitesimally small steps. To describe such a system thermodynamically, one needs to enlarge the thermodynamical state space of the system. In case of a chemical reaction, one must specify the number of particles of each type. The differential of the free energy then generalizes to:

where the
 are the numbers of particles of type j and the
are the numbers of particles of type j and the  are the corresponding chemical potential
are the corresponding chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
s. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.
In case there are other external parameters the above equation generalizes to:

Here the
 are the external variables and the
are the external variables and the  the corresponding generalized forces.
the corresponding generalized forces.Relation to the partition function
A system kept at constant volume and temperature is described by the canonical ensembleCanonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
. The probability to find the system in some energy eigenstate r is given by:

where



Z is called the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the system. The fact that the system does not have a unique energy means that the various thermodynamical quantities must be defined as expectation values. In the thermodynamical limit of infinite system size, the relative fluctuations in these averages will go to zero.
The average internal energy of the system is the expectation value of the energy and can be expressed in terms of Z as follows:
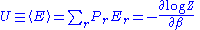
If the system is in state r, then the generalized force corresponding to an external variable x is given by

The thermal average of this can be written as:
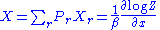
Suppose the system has one external variable x. Then changing the system's temperature parameter by
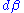 and the external variable by dx will lead to a change in
and the external variable by dx will lead to a change in  :
: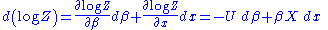
If we write
 as:
as:
we get:
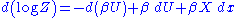
This means that the change in the internal energy is given by:
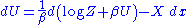
In the thermodynamic limit, the fundamental thermodynamic relation should hold:

This then implies that the entropy of the system is given by:

where c is some constant. The value of c can be determined by considering the limit T → 0. In this limit the entropy becomes
 where
where  is the ground state degeneracy. The partition function in this limit is
is the ground state degeneracy. The partition function in this limit is  where
where 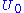 is the ground state energy. Thus, we see that
is the ground state energy. Thus, we see that  and that:
and that: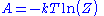
Bogoliubov inequality
Computing the free energy is an intractable problem for all but the simplest models in statistical physics. A powerful approximation method is mean field theoryMean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
, which is a variational method based on the Bogoliubov inequality. This inequality can be formulated as follows.
Suppose we replace the real Hamiltonian
 of the model by a trial Hamiltonian
of the model by a trial Hamiltonian  , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
, which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that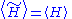
where both averages are taken with respect to the canonical distribution defined by the trial Hamiltonian
 , then
, then
where
 is the free energy of the original Hamiltonian and
is the free energy of the original Hamiltonian and 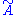 is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.The Bogoliubov inequality is often formulated in a sightly different but equivalent way. If we write the Hamiltonian as:
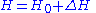
where
 is exactly solvable, then we can apply the above inequality by defining
is exactly solvable, then we can apply the above inequality by defining
Here we have defined
 to be the average of X over the canonical ensemble defined by
to be the average of X over the canonical ensemble defined by  . Since
. Since  defined this way differs from
defined this way differs from 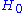 by a constant, we have in general
by a constant, we have in general
Therefore

And thus the inequality
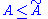
holds. The free energy
 is the free energy of the model defined by
is the free energy of the model defined by 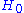 plus
plus  . This means that
. This means that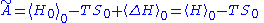
and thus:

Proof
For a classical model we can prove the Bogoliubov inequality as follows. We denote the canonical probability distributions for the Hamiltonian and the trial Hamiltonian by and
and  , respectively. The inequality:
, respectively. The inequality:
then holds. To see this, consider the difference between the left hand side and the right hand side. We can write this as:

Since
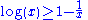
it follows that:

where in the last step we have used that both probability distributions are normalized to 1.
We can write the inequality as:

where the averages are taken with respect to
 . If we now substitute in here the expressions for the probability distributions:
. If we now substitute in here the expressions for the probability distributions:
and

we get:
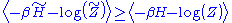
Since the averages of
 and
and  are, by assumption, identical we have:
are, by assumption, identical we have:
Here we have used that the partition functions are constants with respect to taking averages and that the free energy is proportional to minus the logarithm of the partition function.
We can easily generalize this proof to the case of quantum mechanical models. We denote the eigenstates of
 by
by 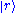 . We denote the diagonal components of the density matrices for the canonical distributions for
. We denote the diagonal components of the density matrices for the canonical distributions for  and
and  in this basis as:
in this basis as:
and

where the
 are the eigenvalues of
are the eigenvalues of 
We assume again that the averages of H and
 in the canonical ensemble defined by
in the canonical ensemble defined by 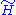 are the same:
are the same:
where

The inequality
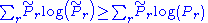
still holds as both the
 and the
and the  sum to 1. On the l.h.s. we can replace:
sum to 1. On the l.h.s. we can replace:
On the right hand side we can use the inequality

where we have introduced the notation

for the expectation value of the operator Y in the state r. See here for a proof. Taking the logarithm of this inequality gives:

This allows us to write:
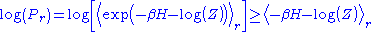
The fact that the averages of H and
 are the same then leads to the same conclusion as in the classical case:
are the same then leads to the same conclusion as in the classical case: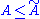
Generalized Helmholtz energy
In the more general case, the mechanical term ( ) must be replaced by the product of the volume times the stress
) must be replaced by the product of the volume times the stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
times an infinitesimal strain:

where
 is the stress tensor, and
is the stress tensor, and  is the strain tensor. In the case of linear elastic
is the strain tensor. In the case of linear elasticElasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
materials that obey Hooke's Law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
, the stress is related to the strain by:

where we are now using Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
for the tensors, in which repeated indices in a product are summed. We may integrate the expression for
 to obtain the Helmholtz energy:
to obtain the Helmholtz energy:

Application to fundamental equations of state
The Helmholtz free energy function for a pure substance (together with its partial derivatives) can be used to determine all other thermodynamic properties for the substance. See, for example, the equations of state for waterWater
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
, as given by the IAPWS
IAPWS
The International Association for the Properties of Water and Steam is an international non-profit association of national organizations concerned with the properties of water and steam, particularly thermophysical properties and other aspects of high-temperature steam, water and aqueous mixtures...
in their IAPWS-95 release.
See also
- Gibbs free energyGibbs free energyIn thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
for thermodynamics history overview and discussion of free energy - Grand potential
- Work contentWork contentIn thermodynamic analysis of chemical reactions, the term free energy denotes either of two related concepts of importance expressing the total amount of energy which is used up or released during a chemical reaction. Both attempt to capture that part of the total energy of a system which is...
- for applications to chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds.... - Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
- This page details the Helmholtz energy from the point of view of thermalThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
and statisticalStatistical physicsStatistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. - Bennett acceptance ratioBennett acceptance ratioThe Bennett acceptance ratio method is an algorithm for estimating the difference in free energy between two systems .It was suggested by Charles H. Bennett in 1976....
for an efficient way to calculate free energy differences, and comparison with other methods.
Further reading
- Atkins' Physical Chemistry, 7th edition, by Peter AtkinsPeter AtkinsPeter William Atkins is a British chemist and former Professor of Chemistry at the University of Oxford and a Fellow of Lincoln College. He is a prolific writer of popular chemistry textbooks, including Physical Chemistry, Inorganic Chemistry, and Molecular Quantum Mechanics...
and Julio de Paula, Oxford University Press
- HyperPhysics Helmholtz Free Energy http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/helmholtz.html

