
Stable map
Encyclopedia
In mathematics
, specifically in symplectic topology
and algebraic geometry
, one can construct the moduli space
of stable maps, satisfying specified conditions, from Riemann surface
s into a given symplectic manifold
. This moduli space is the essence of the Gromov–Witten invariants, which find application in enumerative geometry
and type IIA string theory
. Because the construction is lengthy and difficult, it is carried out here rather than in the Gromov–Witten invariants article itself.
symplectic manifold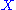 with symplectic form
with symplectic form  . Let
. Let 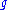 and
and  be natural number
be natural number
s (including zero) and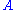 a two-dimensional homology
a two-dimensional homology
class in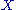 . Then one may consider the set of pseudoholomorphic curve
. Then one may consider the set of pseudoholomorphic curve
s
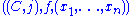
where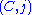 is a smooth, closed Riemann surface
is a smooth, closed Riemann surface
of genus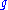 with
with  marked points
marked points  , and
, and
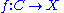
is a function satisfying, for some choice of -tame almost complex structure
-tame almost complex structure
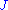 and inhomogeneous term
and inhomogeneous term  , the perturbed Cauchy–Riemann equation
, the perturbed Cauchy–Riemann equation

Typically one admits only those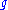 and
and  that make the punctured Euler characteristic
that make the punctured Euler characteristic
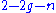 of
of  negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of
negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of  that preserve the marked points.
that preserve the marked points.
The operator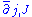 is elliptic
is elliptic
and thus Fredholm
. After significant analytical argument (completing in a suitable Sobolev norm
, applying the implicit function theorem
and Sard's theorem for Banach
manifold
s, and using elliptic regularity to recover smoothness) one can show that, for a generic choice of -tame
-tame 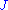 and perturbation
and perturbation  , the set of
, the set of 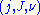 -holomorphic curves of genus
-holomorphic curves of genus 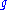 with
with  marked points that represent the class
marked points that represent the class 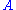 forms a smooth, oriented orbifold
forms a smooth, oriented orbifold
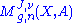
of dimension given by the Atiyah-Singer index theorem,
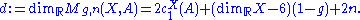
of maps is not compact
, because a sequence of curves can degenerate to a singular curve, which is not in the moduli space as we've defined it. This happens, for example, when the energy of (meaning the L2-norm
(meaning the L2-norm
of the derivative) concentrates at some point on the domain. One can capture the energy by rescaling the map around the concentration point. The effect is to attach a sphere, called a bubble, to the original domain at the concentration point and to extend the map across the sphere. The rescaled map may still have energy concentrating at one or more points, so one must rescale iteratively, eventually attaching an entire bubble tree onto the original domain, with the map well-behaved on each smooth component of the new domain.
In order to make this precise, define a stable map to be a pseudoholomorphic map from a Riemann surface with at worst nodal singularities, such that there are only finitely many automorphisms of the map. Concretely, this means the following. A smooth component of a nodal Riemann surface is said to be stable if there are at most finitely many automorphisms preserving its marked and nodal points. Then a stable map is a pseudoholomorphic map with at least one stable domain component, such that for each of the other domain components
It is significant that the domain of a stable map need not be a stable curve. However, one can contract its unstable components (iteratively) to produce a stable curve, called the stabilization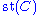 of the domain
of the domain  .
.
The set of all stable maps from Riemann surfaces of genus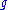 with
with  marked points forms a moduli space
marked points forms a moduli space
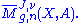
The topology is defined by declaring that a sequence of stable maps converges if and only if
The moduli space of stable maps is compact; that is, any sequence of stable maps converges to a stable map. To show this, one iteratively rescales the sequence of maps. At each iteration there is a new limit domain, possibly singular, with less energy concentration than in the previous iteration. At this step the symplectic form enters in a crucial way. The energy of any smooth map representing the homology class
enters in a crucial way. The energy of any smooth map representing the homology class 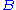 is bounded below by the symplectic area
is bounded below by the symplectic area 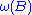 ,
,
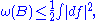
with equality if and only if the map is pseudoholomorphic. This bounds the energy captured in each iteration of the rescaling and thus implies that only finitely many rescalings are needed to capture all of the energy. In the end, the limit map on the new limit domain is stable.
The compactified space is again a smooth, oriented orbifold. Maps with nontrivial automorphisms correspond to points with isotropy in the orbifold.
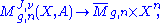

to obtain, under suitable conditions, a rational
homology class
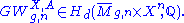
Rational coefficients are necessary because the moduli space is an orbifold. The homology class defined by the evaluation map is independent of the choice of generic -tame
-tame 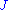 and perturbation
and perturbation  . It is called the Gromov–Witten (GW) invariant of
. It is called the Gromov–Witten (GW) invariant of 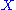 for the given data
for the given data 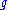 ,
,  , and
, and 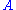 . A cobordism argument can be used to show that this homology class is independent of the choice of
. A cobordism argument can be used to show that this homology class is independent of the choice of  , up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.
, up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.
The "suitable conditions" are rather subtle, primarily because multiply covered maps (maps that factor through a branched covering
of the domain) can form moduli spaces of larger dimension than expected.
The simplest way to handle this is to assume that the target manifold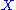 is semipositive or Fano
is semipositive or Fano
in a certain sense. This assumption is chosen exactly so that the moduli space of multiply covered maps has codimension at least two in the space of non-multiply-covered maps. Then the image of the evaluation map forms a pseudocycle, which induces a well-defined homology class of the expected dimension.
Defining Gromov–Witten invariants without assuming some kind of semipositivity requires a difficult, technical construction known as the virtual moduli cycle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, one can construct the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of stable maps, satisfying specified conditions, from Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s into a given symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. This moduli space is the essence of the Gromov–Witten invariants, which find application in enumerative geometry
Enumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...
and type IIA string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. Because the construction is lengthy and difficult, it is carried out here rather than in the Gromov–Witten invariants article itself.
The moduli space of smooth pseudoholomorphic curves
Fix a closedClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
symplectic manifold
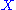 with symplectic form
with symplectic form  . Let
. Let 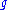 and
and  be natural number
be natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (including zero) and
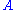 a two-dimensional homology
a two-dimensional homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
class in
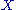 . Then one may consider the set of pseudoholomorphic curve
. Then one may consider the set of pseudoholomorphic curvePseudoholomorphic curve
In mathematics, specifically in topology and geometry, a pseudoholomorphic curve is a smooth map from a Riemann surface into an almost complex manifold that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of...
s
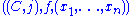
where
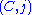 is a smooth, closed Riemann surface
is a smooth, closed Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
of genus
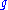 with
with  marked points
marked points  , and
, and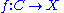
is a function satisfying, for some choice of
 -tame almost complex structure
-tame almost complex structureAlmost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
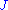 and inhomogeneous term
and inhomogeneous term  , the perturbed Cauchy–Riemann equation
, the perturbed Cauchy–Riemann equation
Typically one admits only those
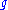 and
and  that make the punctured Euler characteristic
that make the punctured Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
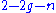 of
of  negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of
negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of  that preserve the marked points.
that preserve the marked points.The operator
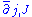 is elliptic
is ellipticElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
and thus Fredholm
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
. After significant analytical argument (completing in a suitable Sobolev norm
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
, applying the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
and Sard's theorem for Banach
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, and using elliptic regularity to recover smoothness) one can show that, for a generic choice of
 -tame
-tame 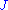 and perturbation
and perturbation  , the set of
, the set of 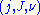 -holomorphic curves of genus
-holomorphic curves of genus 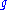 with
with  marked points that represent the class
marked points that represent the class 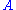 forms a smooth, oriented orbifold
forms a smooth, oriented orbifoldOrbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
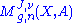
of dimension given by the Atiyah-Singer index theorem,
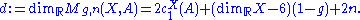
The stable map compactification
This moduli spaceModuli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of maps is not compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, because a sequence of curves can degenerate to a singular curve, which is not in the moduli space as we've defined it. This happens, for example, when the energy of
 (meaning the L2-norm
(meaning the L2-normLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of the derivative) concentrates at some point on the domain. One can capture the energy by rescaling the map around the concentration point. The effect is to attach a sphere, called a bubble, to the original domain at the concentration point and to extend the map across the sphere. The rescaled map may still have energy concentrating at one or more points, so one must rescale iteratively, eventually attaching an entire bubble tree onto the original domain, with the map well-behaved on each smooth component of the new domain.
In order to make this precise, define a stable map to be a pseudoholomorphic map from a Riemann surface with at worst nodal singularities, such that there are only finitely many automorphisms of the map. Concretely, this means the following. A smooth component of a nodal Riemann surface is said to be stable if there are at most finitely many automorphisms preserving its marked and nodal points. Then a stable map is a pseudoholomorphic map with at least one stable domain component, such that for each of the other domain components
- the map is nonconstant on that component, or
- that component is stable.
It is significant that the domain of a stable map need not be a stable curve. However, one can contract its unstable components (iteratively) to produce a stable curve, called the stabilization
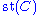 of the domain
of the domain  .
.The set of all stable maps from Riemann surfaces of genus
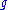 with
with  marked points forms a moduli space
marked points forms a moduli space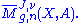
The topology is defined by declaring that a sequence of stable maps converges if and only if
- their (stabilized) domains converge in the Deligne–Mumford moduli space of curves
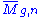 ,
, - they converge uniformly in all derivatives on compact subsets away from the nodes, and
- the energy concentrating at any point equals the energy in the bubble tree attached at that point in the limit map.
The moduli space of stable maps is compact; that is, any sequence of stable maps converges to a stable map. To show this, one iteratively rescales the sequence of maps. At each iteration there is a new limit domain, possibly singular, with less energy concentration than in the previous iteration. At this step the symplectic form
 enters in a crucial way. The energy of any smooth map representing the homology class
enters in a crucial way. The energy of any smooth map representing the homology class 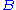 is bounded below by the symplectic area
is bounded below by the symplectic area 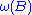 ,
,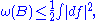
with equality if and only if the map is pseudoholomorphic. This bounds the energy captured in each iteration of the rescaling and thus implies that only finitely many rescalings are needed to capture all of the energy. In the end, the limit map on the new limit domain is stable.
The compactified space is again a smooth, oriented orbifold. Maps with nontrivial automorphisms correspond to points with isotropy in the orbifold.
The Gromov–Witten pseudocycle
To construct Gromov–Witten invariants, one pushes the moduli space of stable maps forward under the evaluation map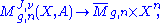

to obtain, under suitable conditions, a rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
homology class
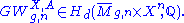
Rational coefficients are necessary because the moduli space is an orbifold. The homology class defined by the evaluation map is independent of the choice of generic
 -tame
-tame 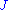 and perturbation
and perturbation  . It is called the Gromov–Witten (GW) invariant of
. It is called the Gromov–Witten (GW) invariant of 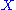 for the given data
for the given data 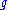 ,
,  , and
, and 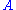 . A cobordism argument can be used to show that this homology class is independent of the choice of
. A cobordism argument can be used to show that this homology class is independent of the choice of  , up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.
, up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.The "suitable conditions" are rather subtle, primarily because multiply covered maps (maps that factor through a branched covering
Branched covering
In mathematics, branched covering is a term mainly used in algebraic geometry, to describe morphisms f from an algebraic variety V to another one W, the two dimensions being the same, and the typical fibre of f being of dimension 0....
of the domain) can form moduli spaces of larger dimension than expected.
The simplest way to handle this is to assume that the target manifold
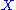 is semipositive or Fano
is semipositive or FanoFano variety
In algebraic geometry, a Fano variety, introduced by , is a non-singular complete variety whose anticanonical bundle is ample.Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces....
in a certain sense. This assumption is chosen exactly so that the moduli space of multiply covered maps has codimension at least two in the space of non-multiply-covered maps. Then the image of the evaluation map forms a pseudocycle, which induces a well-defined homology class of the expected dimension.
Defining Gromov–Witten invariants without assuming some kind of semipositivity requires a difficult, technical construction known as the virtual moduli cycle.

