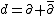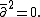Almost complex manifold
Encyclopedia
In mathematics
, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure
on each tangent space
. The existence of this structure is a necessary, but not sufficient, condition for a manifold
to be a complex manifold
. That is, every complex manifold is an almost complex manifold, but not vice-versa. Almost complex structures have important applications in symplectic geometry.
The concept is due to Ehresmann
and Hopf
in the 1940s.
tensor field
J of rank (1,1) such that J 2 = −1 when regarded as a vector bundle
isomorphism
J : TM → TM on the tangent bundle
. A manifold equipped with an almost complex structure is called an almost complex manifold.
If M admits an almost complex structure, it must be even-dimensional. This can be seen as follows. Suppose M is n-dimensional, and let J : TM → TM be an almost complex structure. Then det(J-xI) is a polynomial in x of degree n. If n is odd, then it has a real root, z. Then det(J − zI) = 0, so there exists a vector v in TM with Jv = zv. Hence JJv = z2v which is clearly not equal to −v since z is real. Thus n must be even if M has an almost complex structure. One can show that it must be orientable as well.
An easy exercise in linear algebra
shows that any even dimensional vector space admits a linear complex structure. Therefore an even dimensional manifold always admits a (1, 1) rank tensor pointwise (which is just a linear transformation on each tangent space) such that Jp2 = −1 at each point p. Only when this local tensor can be patched together to be defined globally does the pointwise linear complex structure yield an almost complex structure, which is then uniquely determined. The possibility of this patching, and therefore existence of an almost complex structure on a manifold M is equivalent to a reduction of the structure group
of the tangent bundle from GL(2n, R) to GL(n, C). The existence question is then a purely algebraic topological
one and is fairly well understood.
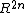 admits an almost complex structure. An example for such an almost complex structure is (
admits an almost complex structure. An example for such an almost complex structure is (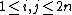 ):
): 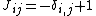 for odd i,
for odd i,
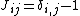 for even i.
for even i.
The only sphere
s which admit almost complex structures are S2 and S6. In the case of S2, the almost complex structure comes from an honest complex structure on the Riemann sphere
. The 6-sphere, S6, when considered as the set of unit norm imaginary octonion
s, inherits an almost complex structure from the octonion multiplication.
Just as we build differential form
s out of exterior powers of the cotangent bundle
, we can build exterior powers of the complexified cotangent bundle (which is canonically isomorphic to the bundle of dual spaces of the complexified tangent bundle). The almost complex structure induces the decomposition of each space of r-forms
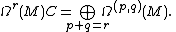
In other words, each Ωr(M)C admits a decomposition into a sum of Ω(p, q)(M), with r = p + q.
As with any direct sum, there is a canonical projection πp,q from Ωr(M)C to Ω(p,q). We also have the exterior derivative
which maps Ωr(M)C to Ωr+1(M)C. Thus we may use the almost complex structure to refine the action of the exterior derivative to the forms of definite type
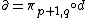
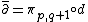
so that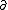 is a map which increases the holomorphic part of the type by one (takes forms of type (p, q) to forms of type (p+1,q)), and
is a map which increases the holomorphic part of the type by one (takes forms of type (p, q) to forms of type (p+1,q)), and 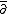 is a map which increases the antiholomorphic part of the type by one. These operators are called the Dolbeault operators.
is a map which increases the antiholomorphic part of the type by one. These operators are called the Dolbeault operators.
Since the sum of all the projections must be the identity map
, we note that the exterior derivative can be written
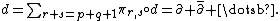
is itself an almost complex manifold. In local holomorphic coordinates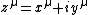 one can define the maps
one can define the maps
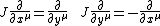
or
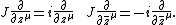
One easily checks that this map defines an almost complex structure. Thus any complex structure on a manifold yields an almost complex structure, which is said to be induced by the complex structure, and the complex structure is said to be compatible with the almost complex structure.
The converse question, whether the almost complex structure implies the existence of a complex structure is much less trivial, and not true in general. On an arbitrary almost complex manifold one can always find coordinates for which the almost complex structure takes the above canonical form at any given point p. In general, however, it is not possible to find coordinates so that J takes the canonical form on an entire neighborhood of p. Such coordinates, if they exist, are called local holomorphic coordinates for J. If M admits local holomorphic coordinates for J around every point then these patch together to form a holomorphic atlas
for M giving it a complex structure, which moreover induces J. J is then said to be integrable. If J is induced by a complex structure, then it is induced by a unique complex structure.
Given any linear map A on each tangent space of M; i.e., A is a tensor field of rank (1, 1), then the Nijenhuis tensor is a tensor field of rank (1,2) given by
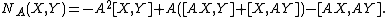
The individual expressions on the right depend on the choice of the smooth vector fields X and Y, but the left side actually depends only on the pointwise values of X and Y, which is why NA is a tensor. This is also clear from the component formula
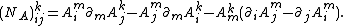
In terms of the Frölicher–Nijenhuis bracket, which generalizes the Lie bracket of vector fields, the Nijenhuis tensor NA is just one-half of [A, A].
The Newlander–Nirenberg theorem states that an almost complex structure J is integrable if and only if NJ = 0. The compatible complex structure is unique, as discussed above. Since the existence of an integrable almost complex structure is equivalent to the existence of a complex structure, this is sometimes taken as the definition of a complex structure.
There are several other criteria which are equivalent to the vanishing of the Nijenhuis tensor, and which therefore furnish methods for checking the integrability of an almost complex structure (and in fact each of these can be found in the literature):
Any of these conditions implies the existence of a unique compatible complex structure.
The existence of an almost complex structure is a topological question and is relatively easy to answer, as discussed above. The existence of an integrable almost complex structure, on the other hand, is a much more difficult analytic question. For example, it has long been known that S6 admits an almost complex structure, but it is still an open question as to whether or not it admits an integrable complex structure.
One should mention that smoothness issues are important. For real-analytic J, the Newlander–Nirenberg theorem follows from the Frobenius theorem
; for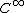 (and less smooth) J, analysis is required (with more difficult techniques as the regularity hypothesis weakens).
(and less smooth) J, analysis is required (with more difficult techniques as the regularity hypothesis weakens).
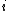 uω = ω(u, •) and the other, denoted φg, is given by the analogous operation for g. With this understood, the three structures (g,ω,J) form a compatible triple when each structure can be specified by the two others as follows:
uω = ω(u, •) and the other, denoted φg, is given by the analogous operation for g. With this understood, the three structures (g,ω,J) form a compatible triple when each structure can be specified by the two others as follows:
In each of these equations, the two structures on the right hand side are called compatible when the corresponding construction yields a structure of the type specified. For example, ω and J are compatible iff ω( •,J • ) is a Riemannian metric. The bundle on M whose sections are the almost complex structures compatible to ω has contractible fibres: the complex structures on the tangent fibres compatible with the restriction to the symplectic forms.
Using elementary properties of the symplectic form ω, one can show that a compatible almost-complex structure J is an almost Kähler structure for the Riemannian metric ω(u,Jv). It is also a fact that if J is integrable, then (M,ω,J) is a Kähler manifold
.
These triples are related to the 2 out of 3 property of the unitary group.
introduced the notion of a generalized almost complex structure on the manifold M, which was elaborated in the doctoral dissertations of his students Marco Gualtieri and Gil Cavalcanti. An ordinary almost complex structure is a choice of a half-dimensional subspace
of each fiber of the complexified tangent bundle
TM. A generalized almost complex structure is a choice of a half-dimensional isotropic subspace of each fiber of the direct sum of the complexified tangent and cotangent bundle
s. In both cases one demands that the direct sum of the subbundle
and its complex conjugate
yield the original bundle.
An almost complex structure integrates to a complex structure if the half-dimensional subspace is closed under the Lie bracket
. A generalized almost complex structure integrates to a generalized complex structure
if the subspace is closed under the Courant bracket
. If furthermore this half-dimensional space is the annihilator of a nowhere vanishing pure spinor
then M is a generalized Calabi–Yau manifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
on each tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
. The existence of this structure is a necessary, but not sufficient, condition for a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to be a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
. That is, every complex manifold is an almost complex manifold, but not vice-versa. Almost complex structures have important applications in symplectic geometry.
The concept is due to Ehresmann
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
and Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
in the 1940s.
Formal definition
Let M be a smooth manifold. An almost complex structure J on M is a linear complex structure (that is, a linear map which squares to −1) on each tangent space of the manifold, which varies smoothly on the manifold. In other words, we have a smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
J of rank (1,1) such that J 2 = −1 when regarded as a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
J : TM → TM on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. A manifold equipped with an almost complex structure is called an almost complex manifold.
If M admits an almost complex structure, it must be even-dimensional. This can be seen as follows. Suppose M is n-dimensional, and let J : TM → TM be an almost complex structure. Then det(J-xI) is a polynomial in x of degree n. If n is odd, then it has a real root, z. Then det(J − zI) = 0, so there exists a vector v in TM with Jv = zv. Hence JJv = z2v which is clearly not equal to −v since z is real. Thus n must be even if M has an almost complex structure. One can show that it must be orientable as well.
An easy exercise in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
shows that any even dimensional vector space admits a linear complex structure. Therefore an even dimensional manifold always admits a (1, 1) rank tensor pointwise (which is just a linear transformation on each tangent space) such that Jp2 = −1 at each point p. Only when this local tensor can be patched together to be defined globally does the pointwise linear complex structure yield an almost complex structure, which is then uniquely determined. The possibility of this patching, and therefore existence of an almost complex structure on a manifold M is equivalent to a reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
of the tangent bundle from GL(2n, R) to GL(n, C). The existence question is then a purely algebraic topological
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
one and is fairly well understood.
Examples
For every integer n, the flat space admits an almost complex structure. An example for such an almost complex structure is (
admits an almost complex structure. An example for such an almost complex structure is (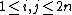 ):
): 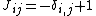 for odd i,
for odd i,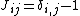 for even i.
for even i.The only sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s which admit almost complex structures are S2 and S6. In the case of S2, the almost complex structure comes from an honest complex structure on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. The 6-sphere, S6, when considered as the set of unit norm imaginary octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, inherits an almost complex structure from the octonion multiplication.
Differential topology of almost complex manifolds
Just as a complex structure on a vector space V allows a decomposition of VC into V+ and V− (the eigenspaces of J corresponding to +i and −i, respectively), so an almost complex structure on M allows a decomposition of the complexified tangent bundle TMC (which is the vector bundle of complexified tangent spaces at each point) into TM+ and TM−. A section of TM+ is called a vector field of type (1,0), while a section of TM− is an vector field of type (0,1). Thus J corresponds to multiplication by i on the (1, 0)-vector fields of the complexified tangent bundle, and multiplication by −i on the (0, 1)-vector fields.Just as we build differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s out of exterior powers of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, we can build exterior powers of the complexified cotangent bundle (which is canonically isomorphic to the bundle of dual spaces of the complexified tangent bundle). The almost complex structure induces the decomposition of each space of r-forms
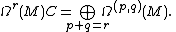
In other words, each Ωr(M)C admits a decomposition into a sum of Ω(p, q)(M), with r = p + q.
As with any direct sum, there is a canonical projection πp,q from Ωr(M)C to Ω(p,q). We also have the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
which maps Ωr(M)C to Ωr+1(M)C. Thus we may use the almost complex structure to refine the action of the exterior derivative to the forms of definite type
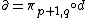
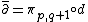
so that
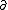 is a map which increases the holomorphic part of the type by one (takes forms of type (p, q) to forms of type (p+1,q)), and
is a map which increases the holomorphic part of the type by one (takes forms of type (p, q) to forms of type (p+1,q)), and 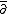 is a map which increases the antiholomorphic part of the type by one. These operators are called the Dolbeault operators.
is a map which increases the antiholomorphic part of the type by one. These operators are called the Dolbeault operators.Since the sum of all the projections must be the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, we note that the exterior derivative can be written
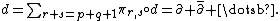
Integrable almost complex structures
Every complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
is itself an almost complex manifold. In local holomorphic coordinates
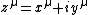 one can define the maps
one can define the maps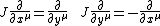
or
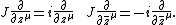
One easily checks that this map defines an almost complex structure. Thus any complex structure on a manifold yields an almost complex structure, which is said to be induced by the complex structure, and the complex structure is said to be compatible with the almost complex structure.
The converse question, whether the almost complex structure implies the existence of a complex structure is much less trivial, and not true in general. On an arbitrary almost complex manifold one can always find coordinates for which the almost complex structure takes the above canonical form at any given point p. In general, however, it is not possible to find coordinates so that J takes the canonical form on an entire neighborhood of p. Such coordinates, if they exist, are called local holomorphic coordinates for J. If M admits local holomorphic coordinates for J around every point then these patch together to form a holomorphic atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
for M giving it a complex structure, which moreover induces J. J is then said to be integrable. If J is induced by a complex structure, then it is induced by a unique complex structure.
Given any linear map A on each tangent space of M; i.e., A is a tensor field of rank (1, 1), then the Nijenhuis tensor is a tensor field of rank (1,2) given by
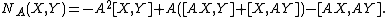
The individual expressions on the right depend on the choice of the smooth vector fields X and Y, but the left side actually depends only on the pointwise values of X and Y, which is why NA is a tensor. This is also clear from the component formula
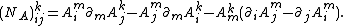
In terms of the Frölicher–Nijenhuis bracket, which generalizes the Lie bracket of vector fields, the Nijenhuis tensor NA is just one-half of [A, A].
The Newlander–Nirenberg theorem states that an almost complex structure J is integrable if and only if NJ = 0. The compatible complex structure is unique, as discussed above. Since the existence of an integrable almost complex structure is equivalent to the existence of a complex structure, this is sometimes taken as the definition of a complex structure.
There are several other criteria which are equivalent to the vanishing of the Nijenhuis tensor, and which therefore furnish methods for checking the integrability of an almost complex structure (and in fact each of these can be found in the literature):
- The Lie bracket of two (1, 0)-vector fields is again of type (1, 0)
Any of these conditions implies the existence of a unique compatible complex structure.
The existence of an almost complex structure is a topological question and is relatively easy to answer, as discussed above. The existence of an integrable almost complex structure, on the other hand, is a much more difficult analytic question. For example, it has long been known that S6 admits an almost complex structure, but it is still an open question as to whether or not it admits an integrable complex structure.
One should mention that smoothness issues are important. For real-analytic J, the Newlander–Nirenberg theorem follows from the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
; for
 (and less smooth) J, analysis is required (with more difficult techniques as the regularity hypothesis weakens).
(and less smooth) J, analysis is required (with more difficult techniques as the regularity hypothesis weakens).Compatible triples
Suppose M is equipped with a symplectic form ω, a Riemannian metric g, and an almost-complex structure J. Since ω and g are nondegenerate, each induces a bundle isomorphism TM → T*M, where the first map, denoted φω, is given by the interior product φω(u) =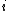 uω = ω(u, •) and the other, denoted φg, is given by the analogous operation for g. With this understood, the three structures (g,ω,J) form a compatible triple when each structure can be specified by the two others as follows:
uω = ω(u, •) and the other, denoted φg, is given by the analogous operation for g. With this understood, the three structures (g,ω,J) form a compatible triple when each structure can be specified by the two others as follows:
- g(u, v) = ω(u, Jv)
- ω(u, v) = g(Ju, v)
- J(u) = φg−1(φω(u)).
In each of these equations, the two structures on the right hand side are called compatible when the corresponding construction yields a structure of the type specified. For example, ω and J are compatible iff ω( •,J • ) is a Riemannian metric. The bundle on M whose sections are the almost complex structures compatible to ω has contractible fibres: the complex structures on the tangent fibres compatible with the restriction to the symplectic forms.
Using elementary properties of the symplectic form ω, one can show that a compatible almost-complex structure J is an almost Kähler structure for the Riemannian metric ω(u,Jv). It is also a fact that if J is integrable, then (M,ω,J) is a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
.
These triples are related to the 2 out of 3 property of the unitary group.
Generalized almost complex structure
Nigel HitchinNigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
introduced the notion of a generalized almost complex structure on the manifold M, which was elaborated in the doctoral dissertations of his students Marco Gualtieri and Gil Cavalcanti. An ordinary almost complex structure is a choice of a half-dimensional subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of each fiber of the complexified tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM. A generalized almost complex structure is a choice of a half-dimensional isotropic subspace of each fiber of the direct sum of the complexified tangent and cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
s. In both cases one demands that the direct sum of the subbundle
Subbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
and its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
yield the original bundle.
An almost complex structure integrates to a complex structure if the half-dimensional subspace is closed under the Lie bracket
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
. A generalized almost complex structure integrates to a generalized complex structure
Generalized complex structure
In the field of mathematics known as differential geometry, a generalized complex structure is a property of a differential manifold that includes as special cases a complex structure and a symplectic structure...
if the subspace is closed under the Courant bracket
Courant bracket
In a field of mathematics known as differential geometry, the Courant bracket is a generalization of the Lie bracket from an operation on the tangent bundle to an operation on the direct sum of the tangent bundle and the vector bundle of p-forms....
. If furthermore this half-dimensional space is the annihilator of a nowhere vanishing pure spinor
Pure spinor
In a field of mathematics known as representation theory pure spinors are spinor representations of the special orthogonal group that are annihilated by the largest possible subspace of the Clifford algebra. They were introduced by Élie Cartan in the 1930s to classify complex structures...
then M is a generalized Calabi–Yau manifold.
See also
- Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
- Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
- Poisson manifoldPoisson manifoldIn mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
- Symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
- Frölicher–Nijenhuis bracket