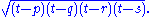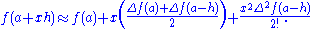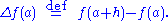Brahmagupta
Encyclopedia
BrahmaguptaBrahmagupta (598–668 CE) was an India
n mathematician
and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta
(Correctly Established Doctrine of Brahma), written in 628 in Bhinmal
. Its 25 chapters contain several unprecedented mathematical results.
city in the state of Rajasthan
of Northwest India. In ancient times Bhillamala was the seat of power of the Gurjars. His father was Jisnugupta. He likely lived most of his life in Bhillamala (modern Bhinmal in Rajasthan
) during the reign (and possibly under the patronage) of King Vyaghramukha. As a result, Brahmagupta is often referred to as Bhillamalacarya, that is, the teacher from Bhillamala. He was the head of the astronomical observatory at Ujjain
, and during his tenure there wrote four texts on mathematics and astronomy: the Cadamekela in 624, the Brahmasphutasiddhanta
in 628, the Khandakhadyaka in 665, and the Durkeamynarda in 672.
The Brahmasphutasiddhanta (Corrected Treatise of Brahma) is arguably his most famous work. The historian al-Biruni
(c. 1050) in his book Tariq al-Hind states that the Abbasid
caliph
al-Ma'mun
had an embassy in India and from India a book was brought to Baghdad which was translated into Arabic as Sindhind. It is generally presumed that Sindhind is none other than Brahmagupta's Brahmasphuta-siddhanta
.
Although Brahmagupta was familiar with the works of astronomers following the tradition of Aryabhatiya
, it is not known if he was familiar with the work of Bhaskara I
, a contemporary. Brahmagupta had a plethora of criticism directed towards the work of rival astronomers, and in his Brahmasphutasiddhanta is found one of the earliest attested schisms among Indian mathematicians. The division was primarily about the application of mathematics to the physical world, rather than about the mathematics itself. In Brahmagupta's case, the disagreements stemmed largely from the choice of astronomical parameters and theories. Critiques of rival theories appear throughout the first ten astronomical chapters and the eleventh chapter is entirely devoted to criticism of these theories, although no criticisms appear in the twelfth and eighteenth chapters.Although we do not know whether Brahmagupta encountered the work of his contemporary Bhaskara, he was certainly aware of the writings of other members of the tradition of the Aryabhatiya, about which he has nothing good to say. This is almost the first trace we possess of the division of Indian astronomer-mathematicians into rival, sometimes antagonistic "schools." [...] it was in the application of mathematical models to the physical world - in this case, the choices of astronomical parameters and theories - that disagreements arose. [...]
Such critiques of rival works appear occasionally throughout the first ten astronomical chapters of the Brahmasphutasiddhanta, and its eleventh chapter is entirely devoted to them. But they do not enter into the mathematical chapters that Brahmagupta devotes respectively to ganita (chapter 12) and the pulverizer (chapter 18). This division of mathematical subjects reflects a different twofold classification from Bhaskara's "mathematics of fields" and "mathematics of quantities." Instead, the first is concerned with arithmetic operations beginning with addition, proportion, interest, series, formulas for finding lengths, areas, and volumes in geometrical figures, and various procedures with fractions - in short, diverse rules for computing with known quantities. The second, on the other hand, deals with what Brahmagupta calls "the pulverizer, zero, negatives, positives, unknowns, elimination of the middle term, reduction to one [variable], bhavita [the product of two unknowns], and the nature of squares [second-degree indeterminate equations]" - that is, techniques for operating with unknown quantities. This distinction is more explicitely presented in later works as mathematics of the "manifest" and "unmanifest," respectively: i.e., what we will henceforth call "arithmetic" manipulations of known quantities and "algebraic" manipulation of so-called "seeds" or unknown quantities. The former, of course, may include geometric problems and other topics not covered by the modern definition of "arithmetic." (Like Aryabhata, Brahmagupta relegates his sine-table to an astronomical chapter where the computations require it, instead of lumping it in with other "mathematical" topics.}}
, and consequently has a poetic ring to it. As no proofs are given, it is not known how Brahmagupta's mathematics was derived.
in chapter eighteen of Brahmasphutasiddhanta,
Which is a solution equivalent to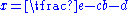
, where rupas represents constants. He further gave two equivalent solutions to the general quadratic equation
,
Which are, respectively, solutions equivalent to,
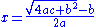
and
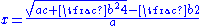
He went on to solve systems of simultaneous indeterminate equations stating that the desired variable must first be isolated, and then the equation must be divided by the desired variable's coefficient
. In particular, he recommended using "the pulverizer" to solve equations with multiple unknowns.
Like the algebra of Diophantus
, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms. The extent of Greek influence on this syncopation
, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.
, 
, 
, 
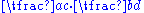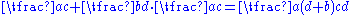, and 
.
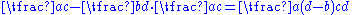It is important to note here Brahmagupta found the result in terms of the sum of the first n integers, rather than in terms of n as is the modern practice.
He gives the sum of the squares of the first n natural numbers as n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as (n(n+1)/2)².
and the Romans
. In chapter eighteen of his Brahmasphutasiddhanta, Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,
He goes on to describe multiplication,
But his description of division by zero
differs from our modern understanding,
Here Brahmagupta states that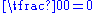
and as for the question of 
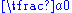where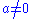 
he did not commit himself. His rules for arithmetic
on negative numbers and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left undefined.
or in other words, for a given length m and an arbitrary multiplier x, let a = mx and b = m + mx/(x + 2). Then m, a, and b form a Pythagorean triple.
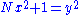(called Pell's equation
) by using the Euclidean algorithm
. The Euclidean algorithm was known to him as the "pulverizer" since it breaks numbers down into ever smaller pieces.
The key to his solution was the identity,
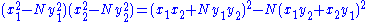
which is a generalization of an identity that was discovered by Diophantus
,
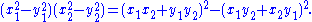
Using his identity and the fact that if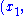
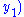and 
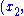
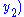are solutions to the equations 
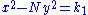and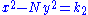 
, respectively, then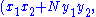 
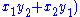is a solution to 
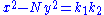, he was able to find integral solutions to the Pell's equation through a series of equations of the form 
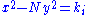. Unfortunately, Brahmagupta was not able to apply his solution uniformly for all possible values of N, rather he was only able to show that if 
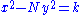has an integral solution for k = ±1, ±2, or ±4, then 
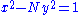has a solution. The solution of the general Pell's equation would have to wait for Bhaskara II in c. 1150 CE.
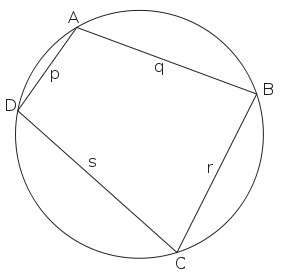Brahmagupta's most famous result in geometry is his formula
for cyclic quadrilaterals. Given the lengths of the sides of any cyclic quadrilateral, Brahmagupta gave an approximate and an exact formula for the figure's area,
So given the lengths p, q, r and s of a cyclic quadrilateral, the approximate area is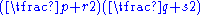
while, letting 
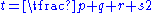, the exact area is
Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is apparent from his rules that this is the case. Heron's formula is a special case of this formula and it can be derived by setting one of the sides equal to zero.
Thus the lengths of the two segments are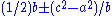
.
He further gives a theorem on rational triangles. A triangle with rational sides a, b, c and rational area is of the form:
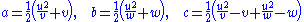
for some rational numbers u, v, and w.
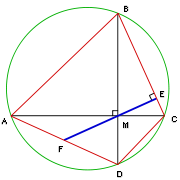Brahmagupta continues,
So, in a "non-unequal" cyclic quadrilateral (that is, an isosceles trapezoid
), the length of each diagonal is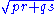
.
He continues to give formulas for the lengths and areas of geometric figures, such as the circumradius of an isosceles trapezoid and a scalene quadrilateral, and the lengths of diagonals in a scalene cyclic quadrilateral. This leads up to Brahmagupta's famous theorem,
,
So Brahmagupta uses 3 as a "practical" value of π, and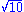
as an "accurate" value of π.
After giving the value of pi, he deals with the geometry of plane figures and solids, such as finding volumes and surface areas (or empty spaces dug out of solids). He finds the volume of rectangular prisms, pyramids, and the frustum of a square pyramid. He further finds the average depth of a series of pits. For the volume of a frustum
of a pyramid, he gives the "pragmatic" value as the depth times the square of the mean of the edges of the top and bottom faces, and he gives the "superficial" volume as the depth times their mean area.
Here Brahmagupta uses names of objects to represent the digits of place-value numerals, as was common with numerical data in Sanskrit treatises. Progenitors represents the 14 Progenitors ("Manu") in Indian cosmology or 14, "twins" means 2, "Ursa Major" represents the seven stars of Ursa Major or 7, "Vedas" refers to the 4 Vedas or 4, dice represents the number of sides of the tradition die or 6, and so on. This information can be translated into the list of sines, 214, 427, 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, and 3270, with the radius being 3270.There are fourteen Progenitors ("Manu") in Indian cosmology; "twins" of course stands for 2; the seven stars of Ursa Major (the "Sages") for 7, the four Vedas, and the four sides of the traditional dice used in gambling, for 6, and so on. Thus Brahmagupta enumerates his first six sine-values as 214, 427, 638, 846, 1051, 1251. (His remaining eighteen sines are 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, 3270. The Paitamahasiddhanta, however, specifies an initial sine-value of 225 (although the rest of its sine-table is lost), implying a trigonometric radius of R = 3438 aprox= C(')/2π: a tradition followed, as we have seen, by Aryabhata. Nobody knows why Brahmagupta chose instead to normalize these values to R = 3270.}}
new values of the sine
function from other values already tabulated. The formula gives an estimate for the value of a function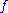
at a value a + xh of its argument (with h > 0 and −1 ≤ x ≤ 1) when its value is already known at a − h, a and a + h.
The formula for the estimate is:
where Δ is the first-order forward-difference operator, i.e.
caliph Al-Mansur
(712–775) founded Baghdad
, which is situated on the banks of the Tigris
, and made it a center of learning. The caliph invited a scholar of Ujjain
by the name of Kankah in 770 A.D. Kankah used the Brahmasphutasiddhanta to explain the Hindu system of arithmetic astronomy. Muhammad al-Fazari
translated Brahmugupta's work into Arabic upon the request of the caliph.
In chapter seven of his Brahmasphutasiddhanta, entitled Lunar Crescent, Brahmagupta rebuts the idea that the Moon is farther from the Earth than the Sun, an idea which is maintained in scriptures. He does this by explaining the illumination of the Moon by the Sun.
He explains that since the Moon is closer to the Earth than the Sun, the degree of the illuminated part of the Moon depends on the relative positions of the Sun and the Moon, and this can be computed from the size of the angle between the two bodies.
Some of the important contributions made by Brahmagupta in astronomy are: methods for calculating the position of heavenly bodies over time (ephemerides
), their rising and setting, conjunction
s, and the calculation of solar and lunar eclipse
s. Brahmagupta criticized the Puranic view that the Earth was flat or hollow. Instead, he observed that the Earth and heaven were spherical and that the Earth is moving. In 1030, the Muslim astronomer
Abu al-Rayhan al-Biruni, in his Ta'rikh al-Hind, later translated into Latin
as Indica, commented on Brahmagupta's work and wrote that critics argued:
According to al-Biruni, Brahmagupta responded to these criticisms with the following argument on gravitation
:
About the Earth's gravity he said: "Bodies fall towards the earth as it is in the nature of the earth to attract bodies, just as it is in the nature of water to flow."
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n mathematician
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
(Correctly Established Doctrine of Brahma), written in 628 in Bhinmal
Bhinmal
Bhinmal is a town in the Jalore District of Rajasthan, India. It is 72 km south of Jalore town. The name Bhinmal is derived from the word Shrimal.Bhinmal was old capital of the kingdom of the Gurjars during medieval period....
. Its 25 chapters contain several unprecedented mathematical results.
Life and work
Brahmagupta is believed to have been born in 598 AD in BhinmalBhinmal
Bhinmal is a town in the Jalore District of Rajasthan, India. It is 72 km south of Jalore town. The name Bhinmal is derived from the word Shrimal.Bhinmal was old capital of the kingdom of the Gurjars during medieval period....
city in the state of Rajasthan
Rajasthan
Rājasthān the land of Rajasthanis, , is the largest state of the Republic of India by area. It is located in the northwest of India. It encompasses most of the area of the large, inhospitable Great Indian Desert , which has an edge paralleling the Sutlej-Indus river valley along its border with...
of Northwest India. In ancient times Bhillamala was the seat of power of the Gurjars. His father was Jisnugupta. He likely lived most of his life in Bhillamala (modern Bhinmal in Rajasthan
Rajasthan
Rājasthān the land of Rajasthanis, , is the largest state of the Republic of India by area. It is located in the northwest of India. It encompasses most of the area of the large, inhospitable Great Indian Desert , which has an edge paralleling the Sutlej-Indus river valley along its border with...
) during the reign (and possibly under the patronage) of King Vyaghramukha. As a result, Brahmagupta is often referred to as Bhillamalacarya, that is, the teacher from Bhillamala. He was the head of the astronomical observatory at Ujjain
Ujjain
Ujjain , is an ancient city of Malwa region in central India, on the eastern bank of the Kshipra River , today part of the state of Madhya Pradesh. It is the administrative centre of Ujjain District and Ujjain Division.In ancient times the city was called Ujjayini...
, and during his tenure there wrote four texts on mathematics and astronomy: the Cadamekela in 624, the Brahmasphutasiddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
in 628, the Khandakhadyaka in 665, and the Durkeamynarda in 672.
The Brahmasphutasiddhanta (Corrected Treatise of Brahma) is arguably his most famous work. The historian al-Biruni
Al-Biruni
Abū al-Rayḥān Muḥammad ibn Aḥmad al-BīrūnīArabic spelling. . The intermediate form Abū Rayḥān al-Bīrūnī is often used in academic literature...
(c. 1050) in his book Tariq al-Hind states that the Abbasid
Abbasid
The Abbasid Caliphate or, more simply, the Abbasids , was the third of the Islamic caliphates. It was ruled by the Abbasid dynasty of caliphs, who built their capital in Baghdad after overthrowing the Umayyad caliphate from all but the al-Andalus region....
caliph
Caliph
The Caliph is the head of state in a Caliphate, and the title for the ruler of the Islamic Ummah, an Islamic community ruled by the Shari'ah. It is a transcribed version of the Arabic word which means "successor" or "representative"...
al-Ma'mun
Al-Ma'mun
Abū Jaʿfar Abdullāh al-Māʾmūn ibn Harūn was an Abbasid caliph who reigned from 813 until his death in 833...
had an embassy in India and from India a book was brought to Baghdad which was translated into Arabic as Sindhind. It is generally presumed that Sindhind is none other than Brahmagupta's Brahmasphuta-siddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
.
Although Brahmagupta was familiar with the works of astronomers following the tradition of Aryabhatiya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
, it is not known if he was familiar with the work of Bhaskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
, a contemporary. Brahmagupta had a plethora of criticism directed towards the work of rival astronomers, and in his Brahmasphutasiddhanta is found one of the earliest attested schisms among Indian mathematicians. The division was primarily about the application of mathematics to the physical world, rather than about the mathematics itself. In Brahmagupta's case, the disagreements stemmed largely from the choice of astronomical parameters and theories. Critiques of rival theories appear throughout the first ten astronomical chapters and the eleventh chapter is entirely devoted to criticism of these theories, although no criticisms appear in the twelfth and eighteenth chapters.Although we do not know whether Brahmagupta encountered the work of his contemporary Bhaskara, he was certainly aware of the writings of other members of the tradition of the Aryabhatiya, about which he has nothing good to say. This is almost the first trace we possess of the division of Indian astronomer-mathematicians into rival, sometimes antagonistic "schools." [...] it was in the application of mathematical models to the physical world - in this case, the choices of astronomical parameters and theories - that disagreements arose. [...]
Such critiques of rival works appear occasionally throughout the first ten astronomical chapters of the Brahmasphutasiddhanta, and its eleventh chapter is entirely devoted to them. But they do not enter into the mathematical chapters that Brahmagupta devotes respectively to ganita (chapter 12) and the pulverizer (chapter 18). This division of mathematical subjects reflects a different twofold classification from Bhaskara's "mathematics of fields" and "mathematics of quantities." Instead, the first is concerned with arithmetic operations beginning with addition, proportion, interest, series, formulas for finding lengths, areas, and volumes in geometrical figures, and various procedures with fractions - in short, diverse rules for computing with known quantities. The second, on the other hand, deals with what Brahmagupta calls "the pulverizer, zero, negatives, positives, unknowns, elimination of the middle term, reduction to one [variable], bhavita [the product of two unknowns], and the nature of squares [second-degree indeterminate equations]" - that is, techniques for operating with unknown quantities. This distinction is more explicitely presented in later works as mathematics of the "manifest" and "unmanifest," respectively: i.e., what we will henceforth call "arithmetic" manipulations of known quantities and "algebraic" manipulation of so-called "seeds" or unknown quantities. The former, of course, may include geometric problems and other topics not covered by the modern definition of "arithmetic." (Like Aryabhata, Brahmagupta relegates his sine-table to an astronomical chapter where the computations require it, instead of lumping it in with other "mathematical" topics.}}
Mathematics
Brahmagupta was the first to use zero as a number. He gave rules to compute with zero. Brahmagupta used negative numbers and zero for computing. The modern rule that two negative numbers multiplied together equals a positive number first appears in Brahmasputa siddhanta. Brahmagupta's most famous work is his Brahmasphutasiddhanta. It is composed in elliptic verse, as was common practice in Indian mathematicsIndian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, and consequently has a poetic ring to it. As no proofs are given, it is not known how Brahmagupta's mathematics was derived.
Algebra
Brahmagupta gave the solution of the general linear equationLinear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
in chapter eighteen of Brahmasphutasiddhanta,
The difference between rupas, when inverted and divided by the difference of the unknowns, is the unknown in the equation. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.
Which is a solution equivalent to
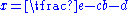, where rupas represents constants. He further gave two equivalent solutions to the general quadratic equationQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
,
18.44. Diminish by the middle [number] the square-root of the rupas multiplied by four times the square and increased by the square of the middle [number]; divide the remainder by twice the square. [The result is] the middle [number].
18.45. Whatever is the square-root of the rupas multiplied by the square [and] increased by the square of half the unknown, diminish that by half the unknown [and] divide [the remainder] by its square. [The result is] the unknown.
Which are, respectively, solutions equivalent to,
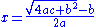
and
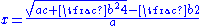
He went on to solve systems of simultaneous indeterminate equations stating that the desired variable must first be isolated, and then the equation must be divided by the desired variable's coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
. In particular, he recommended using "the pulverizer" to solve equations with multiple unknowns.
18.51. Subtract the colors different from the first color. [The remainder] divided by the first [color's coefficient] is the measure of the first. [Terms] two by two [are] considered [when reduced to] similar divisors, [and so on] repeatedly. If there are many [colors], the pulverizer [is to be used].
Like the algebra of Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms. The extent of Greek influence on this syncopation
History of algebra
Algebra is a branch of mathematics concerning the study of structure, relation, and quantity. Elementary algebra is the branch that deals with solving for the operands of arithmetic equations. Modern or abstract algebra has its origins as an abstraction of elementary algebra...
, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.
Arithmetic
Four fundamental operations (addition, subtraction, multiplication and division) were known to many cultures before Brahmagupta. This current system is based on on the Hindu Arabic number system and first appeared in Brahmasputa siddhanta. Contrary to popular opinion, the four fundamental operations (addition, subtraction, multiplication and division) did not appear first in BrahmasputhaSiddhanta, but they were already known by the Sumerians at least 2500 BC. But the sumerian methods are not what we use today. In BrahmasputhaSiddhanta, Multiplication was named Gomutrika. In the beginning of chapter twelve of his Brahmasphutasiddhanta, entitled Calculation, Brahmagupta details operations on fractions. The reader is expected to know the basic arithmetic operations as far as taking the square root, although he explains how to find the cube and cube-root of an integer and later gives rules facilitating the computation of squares and square roots. He then gives rules for dealing with five types of combinations of fractions,, , 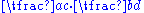, , 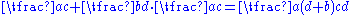and 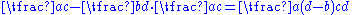.Series
Brahmagupta then goes on to give the sum of the squares and cubes of the first n integers.12.20. The sum of the squares is that [sum] multiplied by twice the [number of] step[s] increased by one [and] divided by three. The sum of the cubes is the square of that [sum] Piles of these with identical balls [can also be computed].
It is important to note here Brahmagupta found the result in terms of the sum of the first n integers, rather than in terms of n as is the modern practice.
He gives the sum of the squares of the first n natural numbers as n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as (n(n+1)/2)².
Zero
Brahmagupta's Brahmasphuṭasiddhanta is the very first book that mentions zero as a number, hence Brahmagupta is considered as the man who found zero. He gave rules of using zero with negative and positive numbers. Zero plus a positive number is the positive number and negative number plus zero is a negative number etc. The Brahmasphutasiddhanta is the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit in representing another number as was done by the Babylonians or as a symbol for a lack of quantity as was done by PtolemyPtolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
and the Romans
Ancient Rome
Ancient Rome was a thriving civilization that grew on the Italian Peninsula as early as the 8th century BC. Located along the Mediterranean Sea and centered on the city of Rome, it expanded to one of the largest empires in the ancient world....
. In chapter eighteen of his Brahmasphutasiddhanta, Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,
18.30. [The sum] of two positives is positives, of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positive, [and that] of two zeros zero.
[...]
18.32. A negative minus zero is negative, a positive [minus zero] positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.
He goes on to describe multiplication,
18.33. The product of a negative and a positive is negative, of two negatives positive, and of positives positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero.
But his description of division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
differs from our modern understanding,
18.34. A positive divided by a positive or a negative divided by a negative is positive; a zero divided by a zero is zero; a positive divided by a negative is negative; a negative divided by a positive is [also] negative.
18.35. A negative or a positive divided by zero has that [zero] as its divisor, or zero divided by a negative or a positive [has that negative or positive as its divisor]. The square of a negative or of a positive is positive; [the square] of zero is zero. That of which [the square] is the square is [its] square-root.
Here Brahmagupta states that
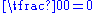and as for the question of 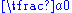where 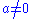he did not commit himself. His rules for arithmeticArithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
on negative numbers and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left undefined.
Pythagorean triples
In chapter twelve of his Brahmasphutasiddhanta, Brahmagupta finds Pythagorean triples,12.39. The height of a mountain multiplied by a given multiplier is the distance to a city; it is not erased. When it is divided by the multiplier increased by two it is the leap of one of the two who make the same journey.
or in other words, for a given length m and an arbitrary multiplier x, let a = mx and b = m + mx/(x + 2). Then m, a, and b form a Pythagorean triple.
Pell's equation
Brahmagupta went on to give a recurrence relation for generating solutions to certain instances of Diophantine equations of the second degree such as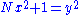 (called Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
) by using the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
. The Euclidean algorithm was known to him as the "pulverizer" since it breaks numbers down into ever smaller pieces.
The nature of squares:
18.64. [Put down] twice the square-root of a given square by a multiplier and increased or diminished by an arbitrary [number]. The product of the first [pair], multiplied by the multiplier, with the product of the last [pair], is the last computed.
18.65. The sum of the thunderbolt products is the first. The additive is equal to the product of the additives. The two square-roots, divided by the additive or the subtractive, are the additive rupas.
The key to his solution was the identity,
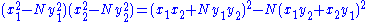
which is a generalization of an identity that was discovered by Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
,
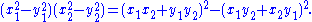
Using his identity and the fact that if
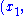
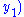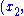
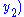and are solutions to the equations 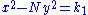and 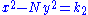, respectively, then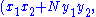 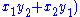is a solution to 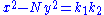, he was able to find integral solutions to the Pell's equation through a series of equations of the form 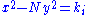. Unfortunately, Brahmagupta was not able to apply his solution uniformly for all possible values of N, rather he was only able to show that if 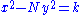has an integral solution for k = ±1, ±2, or ±4, then 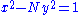has a solution. The solution of the general Pell's equation would have to wait for Bhaskara II in c. 1150 CE.Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
for cyclic quadrilaterals. Given the lengths of the sides of any cyclic quadrilateral, Brahmagupta gave an approximate and an exact formula for the figure's area,
12.21. The approximate area is the product of the halves of the sums of the sides and opposite sides of a triangle and a quadrilateral. The accurate [area] is the square root from the product of the halves of the sums of the sides diminished by [each] side of the quadrilateral.
So given the lengths p, q, r and s of a cyclic quadrilateral, the approximate area is
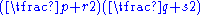while, letting 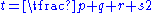, the exact area is
Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is apparent from his rules that this is the case. Heron's formula is a special case of this formula and it can be derived by setting one of the sides equal to zero.
Triangles
Brahmagupta dedicated a substantial portion of his work to geometry. One theorem states that the two lengths of a triangle's base when divided by its altitude then follows,12.22. The base decreased and increased by the difference between the squares of the sides divided by the base; when divided by two they are the true segments. The perpendicular [altitude] is the square-root from the square of a side diminished by the square of its segment.
Thus the lengths of the two segments are
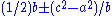.He further gives a theorem on rational triangles. A triangle with rational sides a, b, c and rational area is of the form:
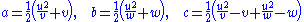
for some rational numbers u, v, and w.
Brahmagupta's theorem
12.23. The square-root of the sum of the two products of the sides and opposite sides of a non-unequal quadrilateral is the diagonal. The square of the diagonal is diminished by the square of half the sum of the base and the top; the square-root is the perpendicular [altitudes].
So, in a "non-unequal" cyclic quadrilateral (that is, an isosceles trapezoid
Trapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
), the length of each diagonal is
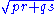.He continues to give formulas for the lengths and areas of geometric figures, such as the circumradius of an isosceles trapezoid and a scalene quadrilateral, and the lengths of diagonals in a scalene cyclic quadrilateral. This leads up to Brahmagupta's famous theorem,
12.30-31. Imaging two triangles within [a cyclic quadrilateral] with unequal sides, the two diagonals are the two bases. Their two segments are separately the upper and lower segments [formed] at the intersection of the diagonals. The two [lower segments] of the two diagonals are two sides in a triangle; the base [of the quadrilateral is the base of the triangle]. Its perpendicular is the lower portion of the [central] perpendicular; the upper portion of the [central] perpendicular is half of the sum of the [sides] perpendiculars diminished by the lower [portion of the central perpendicular].
Pi
In verse 40, he gives values of πPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
,
12.40. The diameter and the square of the radius [each] multiplied by 3 are [respectively] the practical circumference and the area [of a circle]. The accurate [values] are the square-roots from the squares of those two multiplied by ten.
So Brahmagupta uses 3 as a "practical" value of π, and
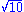as an "accurate" value of π.Measurements and constructions
In some of the verses before verse 40, Brahmagupta gives constructions of various figures with arbitrary sides. He essentially manipulated right triangles to produce isosceles triangles, scalene triangles, rectangles, isosceles trapezoids, isosceles trapezoids with three equal sides, and a scalene cyclic quadrilateral.After giving the value of pi, he deals with the geometry of plane figures and solids, such as finding volumes and surface areas (or empty spaces dug out of solids). He finds the volume of rectangular prisms, pyramids, and the frustum of a square pyramid. He further finds the average depth of a series of pits. For the volume of a frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
of a pyramid, he gives the "pragmatic" value as the depth times the square of the mean of the edges of the top and bottom faces, and he gives the "superficial" volume as the depth times their mean area.
Sine table
In Chapter 2 of his Brahmasphutasiddhanta, entitled Planetary True Longitudes, Brahmagupta presents a sine table:2.2-5. The sines: The Progenitors, twins; Ursa Major, twins, the Vedas; the gods, fires, six; flavors, dice, the gods; the moon, five, the sky, the moon; the moon, arrows, suns [...]
Here Brahmagupta uses names of objects to represent the digits of place-value numerals, as was common with numerical data in Sanskrit treatises. Progenitors represents the 14 Progenitors ("Manu") in Indian cosmology or 14, "twins" means 2, "Ursa Major" represents the seven stars of Ursa Major or 7, "Vedas" refers to the 4 Vedas or 4, dice represents the number of sides of the tradition die or 6, and so on. This information can be translated into the list of sines, 214, 427, 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, and 3270, with the radius being 3270.There are fourteen Progenitors ("Manu") in Indian cosmology; "twins" of course stands for 2; the seven stars of Ursa Major (the "Sages") for 7, the four Vedas, and the four sides of the traditional dice used in gambling, for 6, and so on. Thus Brahmagupta enumerates his first six sine-values as 214, 427, 638, 846, 1051, 1251. (His remaining eighteen sines are 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, 3270. The Paitamahasiddhanta, however, specifies an initial sine-value of 225 (although the rest of its sine-table is lost), implying a trigonometric radius of R = 3438 aprox= C(')/2π: a tradition followed, as we have seen, by Aryabhata. Nobody knows why Brahmagupta chose instead to normalize these values to R = 3270.}}
Interpolation formula
In 665 Brahmagupta devised and used a special case of the Newton–Stirling interpolation formula of the second-order to interpolateInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
new values of the sine
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
function from other values already tabulated. The formula gives an estimate for the value of a function
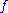at a value a + xh of its argument (with h > 0 and −1 ≤ x ≤ 1) when its value is already known at a − h, a and a + h.The formula for the estimate is:
where Δ is the first-order forward-difference operator, i.e.
Astronomy
It was through the Brahmasphutasiddhanta that the Arabs learned of Indian astronomy. The famous AbbasidAbbasid
The Abbasid Caliphate or, more simply, the Abbasids , was the third of the Islamic caliphates. It was ruled by the Abbasid dynasty of caliphs, who built their capital in Baghdad after overthrowing the Umayyad caliphate from all but the al-Andalus region....
caliph Al-Mansur
Al-Mansur
Al-Mansur, Almanzor or Abu Ja'far Abdallah ibn Muhammad al-Mansur was the second Abbasid Caliph from 136 AH to 158 AH .-Biography:...
(712–775) founded Baghdad
Baghdad
Baghdad is the capital of Iraq, as well as the coterminous Baghdad Governorate. The population of Baghdad in 2011 is approximately 7,216,040...
, which is situated on the banks of the Tigris
Tigris
The Tigris River is the eastern member of the two great rivers that define Mesopotamia, the other being the Euphrates. The river flows south from the mountains of southeastern Turkey through Iraq.-Geography:...
, and made it a center of learning. The caliph invited a scholar of Ujjain
Ujjain
Ujjain , is an ancient city of Malwa region in central India, on the eastern bank of the Kshipra River , today part of the state of Madhya Pradesh. It is the administrative centre of Ujjain District and Ujjain Division.In ancient times the city was called Ujjayini...
by the name of Kankah in 770 A.D. Kankah used the Brahmasphutasiddhanta to explain the Hindu system of arithmetic astronomy. Muhammad al-Fazari
Muhammad al-Fazari
Abu abdallah Muhammad ibn Ibrahim al-Fazari was a Muslim philosopher, mathematician and astronomer. He is not to be confused with his father Ibrāhīm al-Fazārī, also an astronomer and mathematician....
translated Brahmugupta's work into Arabic upon the request of the caliph.
In chapter seven of his Brahmasphutasiddhanta, entitled Lunar Crescent, Brahmagupta rebuts the idea that the Moon is farther from the Earth than the Sun, an idea which is maintained in scriptures. He does this by explaining the illumination of the Moon by the Sun.
7.1. If the moon were above the sun, how would the power of waxing and waning, etc., be produced from calculation of the [longitude of the] moon? the near half [would be] always bright.
7.2. In the same way that the half seen by the sun of a pot standing in sunlight is bright, and the unseen half dark, so is [the illumination] of the moon [if it is] beneath the sun.
7.3. The brightness is increased in the direction of the sun. At the end of a bright [i.e. waxing] half-month, the near half is bright and the far half dark. Hence, the elevation of the horns [of the crescent can be derived] from calculation. [...]
He explains that since the Moon is closer to the Earth than the Sun, the degree of the illuminated part of the Moon depends on the relative positions of the Sun and the Moon, and this can be computed from the size of the angle between the two bodies.
Some of the important contributions made by Brahmagupta in astronomy are: methods for calculating the position of heavenly bodies over time (ephemerides
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
), their rising and setting, conjunction
Conjunction (astronomy)
Conjunction is a term used in positional astronomy and astrology. It means that, as seen from some place , two celestial bodies appear near one another in the sky...
s, and the calculation of solar and lunar eclipse
Eclipse
An eclipse is an astronomical event that occurs when an astronomical object is temporarily obscured, either by passing into the shadow of another body or by having another body pass between it and the viewer...
s. Brahmagupta criticized the Puranic view that the Earth was flat or hollow. Instead, he observed that the Earth and heaven were spherical and that the Earth is moving. In 1030, the Muslim astronomer
Islamic astronomy
Islamic astronomy or Arabic astronomy comprises the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age , and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and...
Abu al-Rayhan al-Biruni, in his Ta'rikh al-Hind, later translated into Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
as Indica, commented on Brahmagupta's work and wrote that critics argued:
According to al-Biruni, Brahmagupta responded to these criticisms with the following argument on gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
:
About the Earth's gravity he said: "Bodies fall towards the earth as it is in the nature of the earth to attract bodies, just as it is in the nature of water to flow."
See also
- Brahmagupta–Fibonacci identity
- Brahmagupta's formulaBrahmagupta's formulaIn Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
- Brahmagupta theoremBrahmagupta theoremBrahmagupta's theorem is a result in geometry. It states that if a cyclic quadrilateral is orthodiagonal , then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side...
- Chakravala methodChakravala methodThe chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
External links
- Brahmagupta's Biography
- Brahmagupta's Brahma-sphuta-siddhanta English introduction, Sanskrit text, Sanskrit and Hindi commentaries (PDF)