Infinite descent
Encyclopedia
In mathematics
, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered
. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that is in some sense 'smaller'. Then one must show, usually with greater ease, that the infinite descent implied by having a whole sequence of solutions that are ever smaller, by our chosen measure, is an impossibility. This is a contradiction
, so no such initial solution can exist.
This illustrative description can be restated in terms of a minimal counterexample
, giving a more common type of formulation of an induction proof. We suppose a 'smallest' solution and then derive a smaller one — thereby getting a contradiction.
The method was developed by and much used for Diophantine equation
s by Fermat. Two typical examples are showing the non-solvability of the Diophantine equation r2 + s4 = t4 and proving that any prime p such that p ≡ 1 (mod. 4) can be expressed as a sum of two squares
. In some cases, to a modern eye, what he was using was (in effect) the doubling mapping on an elliptic curve
. More precisely, his method of infinite descent was an exploitation in particular of the possibility of halving rational points on an elliptic curve E by inversion of the doubling formulae. The context is of a hypothetical rational point on E with large co-ordinates. Doubling a point on E roughly doubles the length of the numbers required to write it (as number of digits): so that a 'halved' point is quite clearly smaller. In this way Fermat was able to show the non-existence of solutions in many cases of Diophantine equations of classical interest (for example, the problem of four perfect squares in arithmetic progression
).
of the twentieth century, the infinite descent method was taken up again, and pushed to a point where it connected with the main thrust of algebraic number theory
and the study of L-function
s. The structural result of Mordell, that the rational points on an elliptic curve E form a finitely-generated abelian group, used an infinite descent argument based on E/2E in Fermat's style.
To extend this to the case of an abelian variety
A, André Weil
had to make more explicit the way of quantifying the size of a solution, by means of a height function - a concept that became foundational. To show that A(Q)/2A(Q) is finite, which is certainly a necessary condition for the finite generation of the group A(Q) of rational points of A, one must do calculations in what later was recognised as Galois cohomology
. In this way, abstractly-defined cohomology groups in the theory become identified with descents in the tradition of Fermat. The Mordell-Weil theorem was at the start of what later became a very extensive theory.
were rational
. Then it could be written as
,
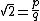for two natural numbers, and . Then,
,
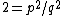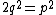, so
.
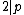We can now write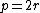
, thus
,
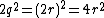, so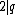
.
Therefore, for both and , smaller natural numbers (which would work equally well to form the rational) can be found by dividing them in half. The same must hold for those smaller numbers, ad infinitum. However, this is impossible in the set of natural numbers
. Since √2 is a real number
, which can be either rational or irrational, the only option left is for √2 to be irrational.
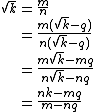
and therefore √k can be expressed in lower terms, which is a contradiction.
Non-solvability of
The non-solvability of 
in integers is sufficient to show the non-solvability of 
in integers, which is a special case of Fermat's Last Theorem
. It can be proven by proving that a Pythagorean triangle cannot have two sides each of which is each either a square or twice a square.
Suppose there exists such a Pythagorean triangle. Then it can be scaled down to give a primitive (i.e., with no common factors) Pythagorean triangle with the same property. Primitive Pythagorean triangles' sides can be written as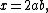
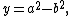
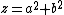, with a and b relatively prime and with a+b odd and hence y and z both odd. But neither y nor z, being odd, can be twice a square; if they are both square, the right triangle with legs 
and 
and 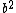hypotenuse 
also would have integer sides including a square leg and a square hypotenuse, and would have a smaller hypotenuse. If y is a square and x is a square or twice a square, then each of a and b is a square or twice a square and the integer right triangle with legs 
and 
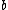and hypotenuse 
would have two sides each of which is a square or twice a square, with a smaller hypotenuse than the original triangle. And if z is a square and x is a square or twice a square, again each of a and b is a square or twice a square and the integer right triangle with legs 
and 
and hypotenuse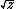 
also would have two sides each of which is a square or twice a square, and a smaller hypotenuse. In any of these cases, one Pythagorean triangle with two sides each of which is a square or twice a square has led to a smaller one, which in turn would lead to a smaller one, etc.; since such a sequence cannot go on infinitely, the original premise that such a triangle exists must be wrong. This implies that 
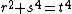cannot have a solution, since if it did then r, s2, and t2 would be the sides of such a Pythagorean triangle.
For other proofs of this by infinite descent, see and .
,
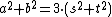other than
.
Suppose there is a nontrivial integer solution of the equation. Then there is a nontrivial nonnegative integer solution obtained by replacing each of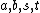
by its absolute value. So it suffices to show that there are no nontrivial nonnegative integer solutions.
Suppose that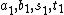
is a nonnegative solution. We have
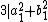
This is only true if both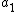
and 
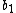are divisible by 3. Let
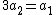and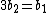 
.
Thus we have
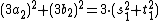
and
,
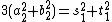which yields a new nontrivial nonnegative integer solution s1, t1, a2, b2. Under a suitable notion of size of the solutions, e.g. the sum of the four integers, this new solution is smaller than the original one. This process can be repeated infinitely, producing an infinite decreasing sequence of positive solution sizes. This is a contradiction, because no such sequence exists. This shows that there are no nonzero solutions for this Diophantine equation
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that is in some sense 'smaller'. Then one must show, usually with greater ease, that the infinite descent implied by having a whole sequence of solutions that are ever smaller, by our chosen measure, is an impossibility. This is a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
, so no such initial solution can exist.
This illustrative description can be restated in terms of a minimal counterexample
Minimal counterexample
In mathematics, the method of considering a minimal counterexample combines the ideas of inductive proof and proof by contradiction. Abstractly, in trying to prove a proposition P, one assumes that it is false, and that therefore there is at least one counterexample...
, giving a more common type of formulation of an induction proof. We suppose a 'smallest' solution and then derive a smaller one — thereby getting a contradiction.
The method was developed by and much used for Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s by Fermat. Two typical examples are showing the non-solvability of the Diophantine equation r2 + s4 = t4 and proving that any prime p such that p ≡ 1 (mod. 4) can be expressed as a sum of two squares
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
. In some cases, to a modern eye, what he was using was (in effect) the doubling mapping on an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
. More precisely, his method of infinite descent was an exploitation in particular of the possibility of halving rational points on an elliptic curve E by inversion of the doubling formulae. The context is of a hypothetical rational point on E with large co-ordinates. Doubling a point on E roughly doubles the length of the numbers required to write it (as number of digits): so that a 'halved' point is quite clearly smaller. In this way Fermat was able to show the non-existence of solutions in many cases of Diophantine equations of classical interest (for example, the problem of four perfect squares in arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
).
Number theory
In the number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
of the twentieth century, the infinite descent method was taken up again, and pushed to a point where it connected with the main thrust of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
and the study of L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s. The structural result of Mordell, that the rational points on an elliptic curve E form a finitely-generated abelian group, used an infinite descent argument based on E/2E in Fermat's style.
To extend this to the case of an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
A, André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
had to make more explicit the way of quantifying the size of a solution, by means of a height function - a concept that became foundational. To show that A(Q)/2A(Q) is finite, which is certainly a necessary condition for the finite generation of the group A(Q) of rational points of A, one must do calculations in what later was recognised as Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
. In this way, abstractly-defined cohomology groups in the theory become identified with descents in the tradition of Fermat. The Mordell-Weil theorem was at the start of what later became a very extensive theory.
Irrationality of √2
Suppose that √2Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
were rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. Then it could be written as
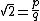,for two natural numbers, and . Then,
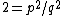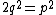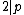,, so.We can now write
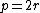, thus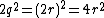,, so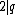.Therefore, for both and , smaller natural numbers (which would work equally well to form the rational) can be found by dividing them in half. The same must hold for those smaller numbers, ad infinitum. However, this is impossible in the set of natural numbers
Well-ordering principle
The "well-ordering principle" is a property of ordered sets. A set X is well ordered if every subset of X has a least element. An example of a well ordered set is the set of natural numbers. An example of set that is not well ordered is the set of integers...
. Since √2 is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, which can be either rational or irrational, the only option left is for √2 to be irrational.
Irrationality of √k if it is not an integer
For positive integer k, suppose that √k is not an integer, but is rational. Then express it in lowest possible terms (i.e., as a fully reduced fraction) as m⁄n for natural numbers m and n, and let q be the largest integer no greater than √k. Then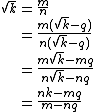and therefore √k can be expressed in lower terms, which is a contradiction.
Non-solvability of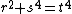 
The non-solvability of in integers is sufficient to show the non-solvability of in integers, which is a special case of Fermat's Last TheoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
. It can be proven by proving that a Pythagorean triangle cannot have two sides each of which is each either a square or twice a square.
Suppose there exists such a Pythagorean triangle. Then it can be scaled down to give a primitive (i.e., with no common factors) Pythagorean triangle with the same property. Primitive Pythagorean triangles' sides can be written as
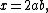
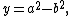
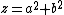, with a and b relatively prime and with a+b odd and hence y and z both odd. But neither y nor z, being odd, can be twice a square; if they are both square, the right triangle with legs and and 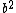hypotenuse also would have integer sides including a square leg and a square hypotenuse, and would have a smaller hypotenuse. 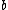If y is a square and x is a square or twice a square, then each of a and b is a square or twice a square and the integer right triangle with legs and and hypotenuse would have two sides each of which is a square or twice a square, with a smaller hypotenuse than the original triangle. And if z is a square and x is a square or twice a square, again each of a and b is a square or twice a square and the integer right triangle with legs and and hypotenuse 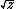also would have two sides each of which is a square or twice a square, and a smaller hypotenuse. In any of these cases, one Pythagorean triangle with two sides each of which is a square or twice a square has led to a smaller one, which in turn would lead to a smaller one, etc.; since such a sequence cannot go on infinitely, the original premise that such a triangle exists must be wrong. This implies that 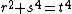cannot have a solution, since if it did then r, s2, and t2 would be the sides of such a Pythagorean triangle.For other proofs of this by infinite descent, see and .
Non-solvability of a2 + b2 = 3(s2 + t2)
Infinite descent can be used to show that there are no integer solutions to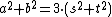,other than
.Suppose there is a nontrivial integer solution of the equation. Then there is a nontrivial nonnegative integer solution obtained by replacing each of
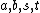by its absolute value. So it suffices to show that there are no nontrivial nonnegative integer solutions.Suppose that
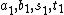is a nonnegative solution. We have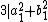This is only true if both
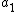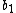and are divisible by 3. Let 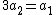and 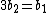.Thus we have
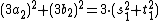
and
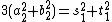,which yields a new nontrivial nonnegative integer solution s1, t1, a2, b2. Under a suitable notion of size of the solutions, e.g. the sum of the four integers, this new solution is smaller than the original one. This process can be repeated infinitely, producing an infinite decreasing sequence of positive solution sizes. This is a contradiction, because no such sequence exists. This shows that there are no nonzero solutions for this Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
.