
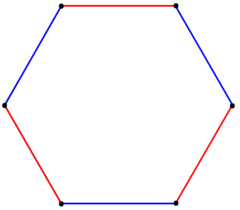
Hexagon
Encyclopedia
{2}t^2
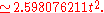
| angle = 120°
| dual =
| properties = convex
, cyclic, equilateral
, isogonal, isotoxal
}}
In geometry
, a hexagon (from Greek
ἕξ hex, 'six') is a polygon
with six edges and six vertices
. A regular hexagon has Schläfli symbol {6}. The total of the internal angles of any hexagon is 720 degrees.
s are 120°
. A regular hexagon has 6 rotational symmetries
(rotational symmetry of order six) and 6 reflection symmetries
(six lines of symmetry), making up the dihedral group
D6. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle
with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.
Like square
s and equilateral
triangle
s, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellation
s.
The cells of a beehive
honeycomb
are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram
of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.
The area of a regular hexagon of side length is given by
is given by
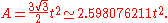
An alternative formula for area is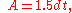 where the length d is the distance between the parallel sides, or the height of the hexagon when it sits on one side as base, or the diameter of the inscribed circle.
where the length d is the distance between the parallel sides, or the height of the hexagon when it sits on one side as base, or the diameter of the inscribed circle.
The area can also be found by the formulas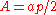 and
and 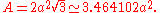 , where a is the apothem
, where a is the apothem
and p is the perimeter.
The perimeter of a regular hexagon of side length is
is  , its maximal diameter
, its maximal diameter  , and its minimal diameter
, and its minimal diameter 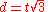 .
.
If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumscribing circle between B and C, then PE + PF = PA + PB + PC + PD.
(also known as the Hexagrammum Mysticum Theorem) states that if an arbitrary hexagon is inscribed in any conic section
, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.
states that the three main diagonals AD, BE, and CF intersect at a single point.
for these regular
and uniform polytope
s, shown in these skew orthogonal projections:
made of regular hexagons, because the hexagons tesselate, not allowing the result to "fold up". The Archimedean solid
s with some hexagonal faces are the truncated tetrahedron
, truncated octahedron
, truncated icosahedron
(of soccer ball and fullerene
fame), truncated cuboctahedron
and the truncated icosidodecahedron
.
And 9 Johnson solid
s:
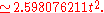
| angle = 120°
| dual =
| properties = convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
, cyclic, equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
, isogonal, isotoxal
}}
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hexagon (from Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
ἕξ hex, 'six') is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with six edges and six vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. A regular hexagon has Schläfli symbol {6}. The total of the internal angles of any hexagon is 720 degrees.
Regular hexagon
A regular hexagon has all sides of the same length, and all internal angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are 120°
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
. A regular hexagon has 6 rotational symmetries
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
(rotational symmetry of order six) and 6 reflection symmetries
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
(six lines of symmetry), making up the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D6. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.
Like square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s and equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s.
The cells of a beehive
Beehive (beekeeping)
A beehive is an enclosed structure in which some honey bee species of the subgenus Apis live and raise their young. Natural beehives are naturally occurring structures occupied by honeybee colonies, while domesticated honeybees live in man-made beehives, often in an apiary. These man-made...
honeycomb
Honeycomb
A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...
are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.
The area of a regular hexagon of side length
 is given by
is given by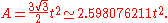
An alternative formula for area is
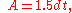 where the length d is the distance between the parallel sides, or the height of the hexagon when it sits on one side as base, or the diameter of the inscribed circle.
where the length d is the distance between the parallel sides, or the height of the hexagon when it sits on one side as base, or the diameter of the inscribed circle.The area can also be found by the formulas
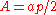 and
and 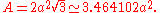 , where a is the apothem
, where a is the apothemApothem
The apothem of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides. The word "apothem" can also refer to the length of that line segment. Regular polygons...
and p is the perimeter.
The perimeter of a regular hexagon of side length
 is
is  , its maximal diameter
, its maximal diameter  , and its minimal diameter
, and its minimal diameter 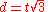 .
.If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumscribing circle between B and C, then PE + PF = PA + PB + PC + PD.
Cyclic hexagon
A cyclic hexagon is any hexagon inscribed in a circle. If the successive sides of the cyclic hexagon are a, b, c, d, e, f, then the three main diagonals intersect in a single point if and only if ace=bdf.Hexagon inscribed in a conic section
Pascal's theoremPascal's theorem
In projective geometry, Pascal's theorem states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.- Related results :This theorem...
(also known as the Hexagrammum Mysticum Theorem) states that if an arbitrary hexagon is inscribed in any conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.
Hexagon tangential to a conic section
Let ABCDEF be a hexagon formed by six tangent lines of a conic section. Then Brianchon's theoremBrianchon's theorem
In geometry, Brianchon's theorem, named after Charles Julien Brianchon , is as follows. Let ABCDEF be a hexagon formed by six tangent lines of a conic section...
states that the three main diagonals AD, BE, and CF intersect at a single point.
Related figures
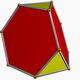
 A regular hexagon can also be created as a truncated Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... equilateral triangle, with Schläfli symbol t{3}. This form only has D3 symmetry. In this figure, the remaining edges of the original triangle are drawn blue, and new edges from the truncation are red. |
 The hexagram can be created as a stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... process: extending the 6 edges of a regular hexagon until they meet at 6 new vertices. |
A concave hexagon |
A self-intersecting hexagon (star polygon) |
A (nonplanar) skew regular hexagon, within the edges of a cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
Petrie polygons
The regular hexagon is the Petrie polygonPetrie polygon
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...
for these regular
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
and uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s, shown in these skew orthogonal projections:
| (3D) | (5D) | |||
|---|---|---|---|---|
Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
5-simplex |
Rectified 5-simplex |
Birectified 5-simplex |
Polyhedra with hexagons
There is no platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
made of regular hexagons, because the hexagons tesselate, not allowing the result to "fold up". The Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s with some hexagonal faces are the truncated tetrahedron
Truncated tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
, truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
, truncated icosahedron
Truncated icosahedron
In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
(of soccer ball and fullerene
Fullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
fame), truncated cuboctahedron
Truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
and the truncated icosidodecahedron
Truncated icosidodecahedron
In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
.
| Archimedean solid Archimedean solid In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices... s |
||||
|---|---|---|---|---|
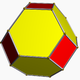
 truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
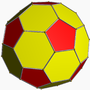 truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
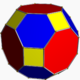 truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
 truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
And 9 Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s:
- triangular cupolaTriangular cupolaIn geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
, elongated triangular cupolaElongated triangular cupolaIn geometry, the elongated triangular cupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a triangular cupola by attaching a hexagonal prism to its base....
, gyroelongated triangular cupolaGyroelongated triangular cupolaIn geometry, the gyroelongated triangular cupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a triangular cupola by attaching a hexagonal antiprism to its base. It can also be seen as a gyroelongated triangular bicupola with one triangular cupola...
, augmented hexagonal prismAugmented hexagonal prismIn geometry, the augmented hexagonal prism is one of the Johnson solids . As the name suggests, it can be constructed by augmenting a hexagonal prism by attaching a square pyramid to one of its equatorial faces....
, parabiaugmented hexagonal prismParabiaugmented hexagonal prismIn geometry, the parabiaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**...
, metabiaugmented hexagonal prismMetabiaugmented hexagonal prismIn geometry, the metabiaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**...
, triaugmented hexagonal prismTriaugmented hexagonal prismIn geometry, the triaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**...
, augmented truncated tetrahedronAugmented truncated tetrahedronIn geometry, the augmented truncated tetrahedron is one of the Johnson solids . It is created by attaching a triangular cupola to one hexagonal face of an truncated tetrahedron.-External links:**...
, triangular hebesphenorotundaTriangular hebesphenorotundaIn geometry, the triangular hebesphenorotunda is one of the Johnson solids . It is one of the elementary Johnson solids, which do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. However, it does have a strong relationship to the icosidodecahedron, an Archimedean...
| Prismoids | ||
|---|---|---|
 Hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
 Hexagonal antiprism Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... |
 Hexagonal pyramid Hexagonal pyramid In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six triangular faces that meet at a point... |
| Other symmetric polyhedra | |||
|---|---|---|---|
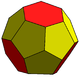 Truncated triakis tetrahedron Truncated triakis tetrahedron The truncated triakis tetrahedron is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps. It is constructed from taking a triakis tetrahedron by truncating the order-6 vertices... |
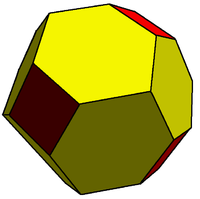 Truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... |
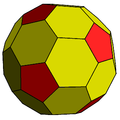 Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... |
 |
Regular and uniform tilings with hexagons
 The hexagon can form a regular tessellate the plane with a Schläfli symbol {6,3}, having 3 hexagons around every vertex. |
 A second hexagonal tessellation of the plane can be formed as a truncated triangular tiling or rhombille tiling, with one of three hexagons colored differently. |
 A third tessellation of the plane can be formed with three colored hexagons around every vertex. |
 Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
|
 Rhombitrihexagonal tiling |
 Truncated trihexagonal tiling |
See also
- Hexagram: 6-sided star within a regular hexagon
- Unicursal hexagramUnicursal HexagramThe unicursal hexagram is a hexagram or six-pointed star that can be traced or drawn unicursally, in one continuous line rather than by two overlaid triangles...
: single path, 6-sided star, within a hexagon - Hexagonal tiling: a regular tiling of hexagons in a plane
- Hexagonal numberHexagonal numberA hexagonal number is a figurate number. The nth hexagonal number will be the number of points in a hexagon with n regularly spaced points on a side.The formula for the nth hexagonal number...
- Hexagonal crystal systemHexagonal crystal systemIn crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families...
- Icositetrachoron: a four-dimensional figure which, like the hexagon, has orthoplex facets and is self-dual
External links
- Definition and properties of a hexagon With interactive animation and construction with compass and straightedge.
- Cymatics - Hexagonal shapes occurring within water sound images
- Cassini Images Bizarre Hexagon on Saturn
- Saturn's Strange Hexagon
- A hexagonal feature around Saturn's North Pole
- "Bizarre Hexagon Spotted on Saturn" - from Space.comSpace.comSpace.com is a space and astronomy news website. Its stories are often syndicated to other media outlets, including CNN, MSNBC, Yahoo!, and USA Today.Space.com was founded by former CNN anchor Lou Dobbs and Rich Zahradnik, in July 1999...
(27 March 2007)

