Degree (angle) - AbsoluteAstronomy.com

This article describes the unit of angle. For other meanings and some specific usages, see degree
Degree
-As a unit of measurement:* Degree symbol, , a notation used in science, engineering and mathematics* Degree , a unit of angle measurement* Degree in geographic coordinate system* Degree , a unit of temperature measurement...

.

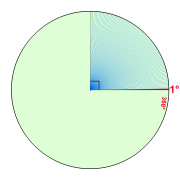
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol

Degree symbol

The degree symbol is a typographical symbol that is used, among other things, to represent degrees of arc or degrees of temperature...

), is a measurement of plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

, representing ¹⁄₃₆₀ of a full rotation

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

; one degree is equivalent to π/180 radian

Radian

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...

s. It is not an SI unit, as the SI unit for angles is radian

Radian

, but it is mentioned in the SI brochure as an accepted unit.

History

The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the stars in the sky, which circle the celestial pole

Celestial pole

The north and south celestial poles are the two imaginary points in the sky where the Earth's axis of rotation, indefinitely extended, intersects the imaginary rotating sphere of stars called the celestial sphere...

every day, seem to advance in that circle by approximately one-360th of a circle, i.e., one degree, each day. Some ancient calendar

Calendar

A calendar is a system of organizing days for social, religious, commercial, or administrative purposes. This is done by giving names to periods of time, typically days, weeks, months, and years. The name given to each day is known as a date. Periods in a calendar are usually, though not...

s, such as the Persian calendar

Iranian calendar

The Iranian calendars or sometimes called Persian calendars are a succession of calendars invented or used for over two millennia in Greater Iran...

, used 360 days for a year. The use of a calendar with 360 days may be related to the use of sexagesimal numbers.

Another theory is that the Babylonians subdivided the circle using the angle of an equilateral triangle as the basic unit and further subdivided the latter into 60 parts following their sexagesimal numeric system. The earliest trigonometry, used by the Babylonian astronomers and their Greek

Greek astronomy

Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the...

successors, was based on chord

Chord (geometry)

A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...

s of a circle. A chord of length equal to the radius made a natural base quantity. One sixtieth of this, using their standard sexagesimal divisions, was a degree.

Aristarchus of Samos

Aristarchus of Samos

Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...

and Hipparchos

Hipparchus

Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...

seem to have been among the first Hellenic scientists to exploit Babylonian astronomical knowledge and techniques systematically. Timocharis

Timocharis

Timocharis of Alexandria was a Greek astronomer and philosopher. Likely born in Alexandria, he was a contemporary of Euclid....

, Aristarchus, Aristillus

Aristillus

Aristillus was a Greek astronomer, presumably of the school of Timocharis . He was among the earliest meridian-astronomy observers....

, Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

, and Hipparchus were the first Greeks known to divide the circle in 360 degrees of 60 arc minutes (DIO 14 ‡2 p.19 n.24). Eratosthenes

Eratosthenes

Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...

used a simpler sexagesimal system dividing a circle into 60 parts.

The division of the circle into 360 parts also occurred in ancient India

India

India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...

, as evidenced in the Rigveda

Rigveda

The Rigveda is an ancient Indian sacred collection of Vedic Sanskrit hymns...

:
Another motivation for choosing the number 360 may have been that it is readily divisible: 360 has 24 divisor

Divisor

In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

s, including every number from 1 to 10 except 7 . This property has many useful applications, such as dividing the world into 24 time zone

Time zone

A time zone is a region on Earth that has a uniform standard time for legal, commercial, and social purposes. In order for the same clock time to always correspond to the same portion of the day as the Earth rotates , different places on the Earth need to have different clock times...

s, each of which is nominally 15° of longitude

Longitude

Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....

, to correlate with the established 24-hour

Hour

The hour is a unit of measurement of time. In modern usage, an hour comprises 60 minutes, or 3,600 seconds...

day

Day

A day is a unit of time, commonly defined as an interval equal to 24 hours. It also can mean that portion of the full day during which a location is illuminated by the light of the sun...

convention.

Finally, it may be the case that more than one of these factors has come into play. According to that theory, the number is approximately 365 because of the apparent movement of the sun against the celestial sphere and that it was rounded to 360 for some of the mathematical reasons cited above.

Subdivisions

For many practical purposes, a degree is a small enough angle that whole degrees provide sufficient precision. When this is not the case, as in astronomy

Astronomy

Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...

or for latitude

Latitude

In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...

s and longitude

Longitude

s on the Earth, degree measurements may be written with decimal

Decimal

The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....

places like 40.1875° with the degree symbol behind the decimals.

Alternatively, the traditional sexagesimal unit

Units of measurement

A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...

subdivision can be used. One degree is divided into 60 minutes (of arc), and one minute into 60 seconds (of arc). These units, also called the arcminute and arcsecond, are respectively represented as a single and double prime

Prime (symbol)

The prime symbol , double prime symbol , and triple prime symbol , etc., are used to designate several different units, and for various other purposes in mathematics, the sciences and linguistics...

: for example, 40.1875° = 40° 11′ 15″ . Sometimes single and double quotation marks are used instead: 40° 11' 15" .

If still more accuracy is required, current practice is to use decimal divisions of the second like 40° 11′ 15.4″ . The older system of thirds, fourths, etc., which continues the sexagesimal unit subdivision, was used by al-Kashi and other ancient astronomers, but is rarely used today. These subdivisions were denoted by writing the Roman numeral for the number of sixtieths in superscript: 1^I for a "prime" (minute of arc), 1^II for a second, 1^III for a third, 1^IV for a fourth, etc. Hence the modern symbols for the minute and second of arc, and the word "second" also refer to this system.

Alternative units

In most mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

work beyond practical geometry, angles are typically measured in radian

Radian

s rather than degrees. This is for a variety of reasons; for example, the trigonometric function

Trigonometric function

In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...

s have simpler and more "natural" properties when their arguments are expressed in radians. These considerations outweigh the convenient divisibility of the number 360. One complete turn

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

(360°) is equal to 2π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

radians, so 180° is equal to π radians, or equivalently, the degree is a mathematical constant

Mathematical constant

A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...

: 1° = ^π⁄₁₈₀.

The turn

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

(or revolution, full circle, full rotation, cycle) is used in technology and science. 1 turn = 360°.

With the invention of the metric system

Metric system

The metric system is an international decimalised system of measurement. France was first to adopt a metric system, in 1799, and a metric system is now the official system of measurement, used in almost every country in the world...

, based on powers of ten, there was an attempt to define a "decimal degree" (grad
Grad (angle)
The gradian is a unit of plane angle, equivalent to of a turn. It is also known as gon, grad, or grade . One grad equals of a degree or of a radian...

or gon), so that the number of decimal degrees in a right angle would be 100 gon, and there would be 400 gon in a circle. Although this idea was abandoned already by Napoleon, some groups have continued to use it and many scientific calculator

Calculator

An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...

s still support it.

An angular mil

Angular mil

An angular mil, also mil, is a unit of angle. All versions of the angular mil are approximately the same size as a trigonometric milliradian.-History:The milliradian was first identified in the mid nineteenth Century...

, which is most used in military applications, has at least three specific variants, ranging from to , each approximately equal to one milliradian. However, used by the Russian Army originated in Imperial Russia, where an equilateral chord was divided into tenths to give a circle of 600 units (this may be seen on a uglomer, circa 1900, in the St Petersberg Museum of Artillery).

Conversion of some common angles

Units	\| Values
Turns Turn (geometry) A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....	0							1
Degrees	0°	30°	45°	60°	90°	180°	270°	360°
Radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... s	0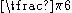
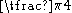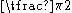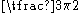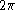Grads Grad (angle) The gradian is a unit of plane angle, equivalent to of a turn. It is also known as gon, grad, or grade . One grad equals of a degree or of a radian...	0^g	33⅓^g	50^g	66⅔^g	100^g	200^g	300^g	400^g

External links

Degrees as an angle measure, with interactive animation
Degree at MathWorld
MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Subdivisions

Alternative units

Conversion of some common angles

See also

External links