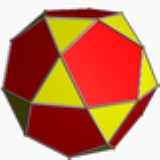
Truncated icosidodecahedron
Encyclopedia
In geometry
, the truncated icosidodecahedron is an Archimedean solid
, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon
face
s.
It has 30 square
faces, 20 regular hexagonal faces, 12 regular decagon
al faces, 120 vertices and 180 edges – more than any other nonprismatic uniform polyhedron
. Since each of its faces has point symmetry (equivalently, 180° rotation
al symmetry), the truncated icosidodecahedron is a zonohedron
.
The name truncated icosidodecahedron, originally given by Johannes Kepler
, is somewhat misleading. If one truncates
an icosidodecahedron
by cutting the corners off, one does not get this uniform figure: instead of square
s the truncation has golden rectangles. However, the resulting figure is topologically
equivalent to this and can always be deformed until the faces are regular.
The alternative name great rhombicosidodecahedron (as well as rhombitruncated icosidodecahedron) refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron
which is dual to the icosidodecahedron
. Compare to small rhombicosidodecahedron.
One unfortunate point of confusion is that there is a nonconvex uniform polyhedron of the same name. See nonconvex great rhombicosidodecahedron.
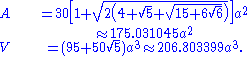
Truncated icosidodecahedron is the largest solid among all 13 Archimedean solids with the same side lengths.
where τ = (1 + √5)/2 is the golden ratio
.
. This projection is conformal
, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated icosidodecahedron is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s.
It has 30 square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
faces, 20 regular hexagonal faces, 12 regular decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
al faces, 120 vertices and 180 edges – more than any other nonprismatic uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
. Since each of its faces has point symmetry (equivalently, 180° rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
al symmetry), the truncated icosidodecahedron is a zonohedron
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
.
Other names
Alternate interchangeable names include:- Truncated icosidodecahedron (Johannes KeplerJohannes KeplerJohannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
) - Rhombitruncated icosidodecahedron (Magnus WenningerMagnus WenningerFather Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...
) - Great rhombicosidodecahedron (Robert WilliamsRobert Williams (geometer)Robert Edward Williams is an American designer, mathematician, and architect. He is noted for books on the geometry of natural structure, the discovery of a new space-filling polyhedron, the development of theoretical principles of Catenatic Geometry, and the invention of the Ars-Vivant Wild-life...
, Peter Cromwell) - OmnitruncatedOmnitruncation (geometry)In geometry, an omnitruncation is an operation applied to a regular polytope in a Wythoff construction that creates a maximum number of facets...
dodecahedron or icosahedron (Norman Johnson)
The name truncated icosidodecahedron, originally given by Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, is somewhat misleading. If one truncates
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
an icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
by cutting the corners off, one does not get this uniform figure: instead of square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s the truncation has golden rectangles. However, the resulting figure is topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
equivalent to this and can always be deformed until the faces are regular.
 Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
A literal geometric truncation Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... of the icosidodecahedron produces rectangular Rectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... faces rather than squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... . |
The alternative name great rhombicosidodecahedron (as well as rhombitruncated icosidodecahedron) refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
which is dual to the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
. Compare to small rhombicosidodecahedron.
One unfortunate point of confusion is that there is a nonconvex uniform polyhedron of the same name. See nonconvex great rhombicosidodecahedron.
Area and volume
The surface area A and the volume V of the truncated icosidodecahedron of edge length a are: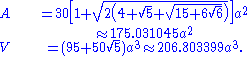
Truncated icosidodecahedron is the largest solid among all 13 Archimedean solids with the same side lengths.
Cartesian coordinates
Cartesian coordinates for the vertices of a truncated icosidodecahedron with edge length 2τ − 2, centered at the origin, are all the even permutations of:- (±1/τ, ±1/τ, ±(3+τ)),
- (±2/τ, ±τ, ±(1+2τ)),
- (±1/τ, ±τ2, ±(−1+3τ)),
- (±(-1+2τ), ±2, ±(2+τ)) and
- (±τ, ±3, ±2τ),
where τ = (1 + √5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Orthogonal projections
The truncated icosidodecahedron has seven special orthogonal projections, centered on a vertex, on three types of edges, and three types of faces: square, hexagonal and decagonal. The last two correspond to the A2 and H2 Coxeter planes.| Centered by | Vertex | Edge 4-6 |
Edge 4-10 |
Edge 6-10 |
Face square |
Face hexagon |
Face decagon |
|---|---|---|---|---|---|---|---|
| Image | |||||||
| Projective symmetry |
[2]+ | [2] | [2] | [2] | [2] | [6] | [10] |
Spherical tiling
The truncated icosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. This projection is conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |
Decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... -centered |
Hexagon-centered |
square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... -centered |
| Spherical tiling | Stereographic projections (face-centered) | ||
|---|---|---|---|
See also
- Spinning great rhombicosidodecahedron
- dodecahedron
- great truncated icosidodecahedron
- icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- truncated cuboctahedronTruncated cuboctahedronIn geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
External links
- http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=jyCXwNVGKYhjPzSzHvH6BpWB1nxUllNUTutfUmnrdPCqgG9BfDHVz13yDxyy8ZbPXPYfuhjBgLDKLplZooNgdJytRWTgG9MGZ8jxB7DiK3wuGdDOyavgu12Y4kH9OibG0rtX2DxQy5UK9aRX0DuHn6C1VbRigFvqYXIbanO5FNXQHLTDE6mNNCh9aISfiW559Lk750AhuxmgOLuCn6UNixmnpE2QfOkJbL4PCYRmRpuIUS0QvLwkNqJ9q1F0I9vC5Fnjymc5wvWKYexxMjFeaqDG6Yg8zVPDADeEwOZJJqDpNXsl8m0ggt16OUXDFGtYHoyt5xQaq4zUpO9kofXCerjc8dVJiwH5uspTLVvp43GjR5TmfrHHfP8FxW7BmzeyeRYmAMMbpgYCcjc69XJG9F4owdKUZw7JkSSc1C3n2PAnZdeniInNLUEzmrLH4g4t9zH1R47Ebu57xji7f1sagyoPR6NiY8YZcN5a7oosgqpJSLouSkkJrPMnr5OOaB5NrI5tExTmzZzhIhCbZu8ywPdIW16i3nqv8rLgHaARBptR1nFHzKbepGzxiXCHlID2zJxCCHyYtiQtuI1oAUNNvoqb3oYNogIfxUD5JBb0noHc4n0O4wT3FGqfahAH6P7hPzmpEzTJvXL2klxvqZDFbNIAnMGj5nBvVbgNEjKyaBKcjNTGGbGRROZBn0bdEsPaDdd1WNmT1GAMXZMSw8TnBvk3UuRIcKGut2lijq3I2pkBIwjSMPsb2PMoWriRjzGLMW3G6uQaSCFV66d9LJSg5jOwaQEAsXsOO0fQLurlEfcRb4fK7zfYx01CcGc2cjaYvQvQtKvFQ4eLB9TMs05EaHtbXXJ4NNHXD27zh0jd9TO16gSBgSwwO1bDBp3bVZerWTc9p4wecUpEOW0jbQRQvEXdDmxZ8ABN7rVNJ6lkiRDQlIzpnL3Isus0VzwN8FHLEkdhV7gzFbQr7vrstMacKS5vN26ggaSgJ4PwWjQPOVQBsqY0H8V4DTUuUZ3vojV5jD8cehrj8KSjr71Zqxu&name=Truncated+Icosidodecahedron#appletEditable printable net of a truncated icosidodecahedron with interactive 3D view]
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra

