
Vertex (geometry)
Encyclopedia
In geometry
, a vertex (plural vertices) is a special kind of point
that describes the corner
s or intersection
s of geometric shapes.
is the point where two rays begin or meet, where two line segments join or meet, where two lines intersect (cross), or any appropriate combination of rays, segments and lines that result in two straight "sides" meeting at one place.
, polyhedron
, or other higher dimensional polytope
, formed by the intersection of edges
, faces
or facets of the object.
In a polygon, a vertex is called "convex
" if the internal angle
of the polygon, that is, the angle
formed by the two edges at the vertex, with the polygon inside the angle, is less than π radians; otherwise, it is called "concave" or "reflex". More generally, a vertex of a polyhedron or polytope is convex if the intersection of the polyhedron or polytope with a sufficiently small sphere
centered at the vertex is convex, and concave otherwise.
Polytope vertices are related to vertices of graphs
, in that the 1-skeleton of a polytope is a graph, the vertices of which correspond to the vertices of the polytope, and in that a graph can be viewed as a 1-dimensional simplicial complex the vertices of which are the graph's vertices. However, in graph theory, vertices may have fewer than two incident edges, which is usually not allowed for geometric vertices. There is also a connection between geometric vertices and the vertices of a curve
, its points of extreme curvature: in some sense the vertices of a polygon are points of infinite curvature, and if a polygon is approximated by a smooth curve there will be a point of extreme curvature near each polygon vertex. However, a smooth curve approximation to a polygon will also have additional vertices, at the points where its curvature is minimal.
is a point where three or more tiles meet; generally, but not always, the tiles of a tessellation are polygons and the vertices of the tessellation are also vertices of its tiles. More generally, a tessellation can be viewed as a kind of topological cell complex, as can the faces of a polyhedron or polytope; the vertices of other kinds of complexes such as simplicial complex
es are its zero-dimensional faces.
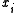 of a simple polygon P is a principal polygon vertex if the diagonal
of a simple polygon P is a principal polygon vertex if the diagonal 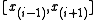 intersects the boundary of P only at
intersects the boundary of P only at 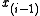 and
and 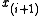 .
.
There are two types of principal vertices: ears and mouths.
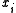 of a simple polygon P is called an ear if the diagonal
of a simple polygon P is called an ear if the diagonal 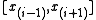 that bridges
that bridges 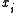 lies entirely in P. (see also convex polygon
lies entirely in P. (see also convex polygon
)
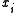 of a simple polygon P is called a mouth if the diagonal
of a simple polygon P is called a mouth if the diagonal  lies outside the boundary of P. (see also concave polygon)
lies outside the boundary of P. (see also concave polygon)
, objects are often represented as triangulated polyhedra
in which the object vertices
are associated not only with three spatial coordinates but also with other graphical information necessary to render the object correctly, such as colors, reflectance properties, textures, and surface normals; these properties are used in rendering by a vertex shader, part of the vertex pipeline
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a vertex (plural vertices) is a special kind of point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
that describes the corner
Corner
A corner is the place where two lines meet at an angle, and a concave corner of intersecting walls is generally thought to be the least beneficial position to be in a life-or-death situation. From this notion was born the verb to corner, which is used to mean "to back into a corner" and usually...
s or intersection
Intersection
Intersection has various meanings in different contexts:*In mathematics and geometry**Intersection , the set of elements common to some collection of sets.**Line-line intersection**Line-plane intersection**Line–sphere intersection...
s of geometric shapes.
Of an angle
The vertex of an angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
is the point where two rays begin or meet, where two line segments join or meet, where two lines intersect (cross), or any appropriate combination of rays, segments and lines that result in two straight "sides" meeting at one place.
Of a polytope
A vertex is a corner point of a polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, or other higher dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
, formed by the intersection of edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
, faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
or facets of the object.
In a polygon, a vertex is called "convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
" if the internal angle
Internal angle
In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon...
of the polygon, that is, the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
formed by the two edges at the vertex, with the polygon inside the angle, is less than π radians; otherwise, it is called "concave" or "reflex". More generally, a vertex of a polyhedron or polytope is convex if the intersection of the polyhedron or polytope with a sufficiently small sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
centered at the vertex is convex, and concave otherwise.
Polytope vertices are related to vertices of graphs
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, in that the 1-skeleton of a polytope is a graph, the vertices of which correspond to the vertices of the polytope, and in that a graph can be viewed as a 1-dimensional simplicial complex the vertices of which are the graph's vertices. However, in graph theory, vertices may have fewer than two incident edges, which is usually not allowed for geometric vertices. There is also a connection between geometric vertices and the vertices of a curve
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
, its points of extreme curvature: in some sense the vertices of a polygon are points of infinite curvature, and if a polygon is approximated by a smooth curve there will be a point of extreme curvature near each polygon vertex. However, a smooth curve approximation to a polygon will also have additional vertices, at the points where its curvature is minimal.
Of a plane tiling
A vertex of a plane tiling or tessellationTessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
is a point where three or more tiles meet; generally, but not always, the tiles of a tessellation are polygons and the vertices of the tessellation are also vertices of its tiles. More generally, a tessellation can be viewed as a kind of topological cell complex, as can the faces of a polyhedron or polytope; the vertices of other kinds of complexes such as simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es are its zero-dimensional faces.
Principal vertex
A polygon vertex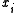 of a simple polygon P is a principal polygon vertex if the diagonal
of a simple polygon P is a principal polygon vertex if the diagonal 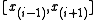 intersects the boundary of P only at
intersects the boundary of P only at 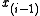 and
and 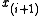 .
.There are two types of principal vertices: ears and mouths.
Ears
A principal vertex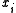 of a simple polygon P is called an ear if the diagonal
of a simple polygon P is called an ear if the diagonal 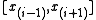 that bridges
that bridges 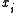 lies entirely in P. (see also convex polygon
lies entirely in P. (see also convex polygonConvex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
)
Mouths
A principal vertex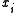 of a simple polygon P is called a mouth if the diagonal
of a simple polygon P is called a mouth if the diagonal  lies outside the boundary of P. (see also concave polygon)
lies outside the boundary of P. (see also concave polygon)Vertices in computer graphics
In computer graphicsComputer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, objects are often represented as triangulated polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
in which the object vertices
Vertex (computer graphics)
A vertex in computer graphics is a data structure that describes a point in 2D or 3D space. Display objects are composed of arrays of flat surfaces and vertices define the location and other attributes of the corners of the surfaces.-Application to object models:In computer graphics, objects are...
are associated not only with three spatial coordinates but also with other graphical information necessary to render the object correctly, such as colors, reflectance properties, textures, and surface normals; these properties are used in rendering by a vertex shader, part of the vertex pipeline
Vertex pipeline
The function of the vertex pipeline in any GPU is to take geometry data , work with it if needed with either fixed function processes , or a vertex shader program , and create all of the 3D data points in a scene to a 2D plane for display on a computer monitor.It is possible to eliminate unneeded...
.

