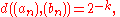Formal power series
Encyclopedia
In mathematics
, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates. This perspective contrasts with that of power series, whose variables designate numerical values, and which series therefore only have a definite value if convergence can be established. Formal power series are often used merely to represent the whole collection of their coefficients. In combinatorics
they provide representations of numerical sequence
s and of multiset
s, and for instance allow giving concise expressions for recursively
defined sequences regardless of whether the recursion can be explicitly solved; this is known as the method of generating function
s.
, but with infinitely many terms. Alternatively, for those familiar with power series (or Taylor series
), one may think of a formal power series as a power series in which we ignore questions of convergence
by not assuming that x denotes any numerical value (not even an unknown value). For example, consider the series

If we studied this as a power series, its properties would include, for example, that its radius of convergence is 1. However, as a formal power series, we may ignore this completely; all that is relevant is the sequence of coefficient
s [1, −3, 5, −7, 9, −11, ...]. In other words, a formal power series is an object that just records a sequence of coefficients. It is perfectly acceptable to consider a formal power series with as coefficients [1, 1, 2, 6 , 24, 120, 720, 5040, … ] (the factorial
s), even though the corresponding power series diverges for any nonzero value of x.
Arithmetic on formal power series is carried out by simply pretending that the series are polynomials. For example, if

then we add A and B term by term:

We can multiply formal power series, again just by treating them as polynomials (see in particular Cauchy product):

Notice that each coefficient in the product AB only depends on a finite number of coefficients of A and B. For example, the x5 term is given by
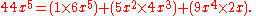
For this reason, one may multiply formal power series without worrying about the usual questions of absolute
, conditional and uniform convergence which arise in dealing with power series in the setting of analysis
.
Once we have defined multiplication for formal power series, we can define multiplicative inverses as follows. The multiplicative inverse of a formal power series A is a formal power series C such that AC = 1, provided that such a formal power series exists. It turns out that if A has a multiplicative inverse, it is unique, and we denote it by A −1. Now we can define division of formal power series by defining B / A to be the product B A −1, provided that the inverse of A exists. For example, one can use the definition of multiplication above to verify the familiar formula
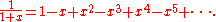
An important operation on formal power series is coefficient extraction. In its most basic form, the coefficient extraction operator for a formal power series in one variable extracts the coefficient of xn, and is written e.g. [xn] A, so that [x2] A = 5 and [x5] A = −11. Other examples include
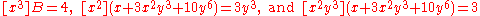
and

Similarly, many other operations that are carried out on polynomials can be extended to the formal power series setting, as explained below.
R form another ring that is written R
ring R[X] equipped with a particular metric
. This automatically gives R
It is possible to describe R
s (taken to include 0). Designating a sequence whose term at index n is an by , one defines addition of two such sequences by
, one defines addition of two such sequences by
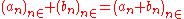
and multiplication by
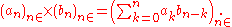
This type of product is called the Cauchy product of the two sequences of coefficients, and is a sort of discrete convolution
. With these operations, RN becomes a commutative ring with zero element (0, 0, 0, ...) and multiplicative identity (1, 0, 0,...).
The product is in fact the same one used to define the product of polynomials in one indeterminate, which suggests using a similar notation. One embeds R into R
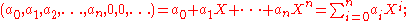
these are precisely the polynomials in X. Given this, it is quite natural and convenient to designate a general sequence an by by the formal expression
by the formal expression 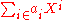 , even though the latter is not an expression formed by the operations of addition and multiplication defined above (from which only finite sums can be constructed). This notational convention allows reformulation the above definitions as
, even though the latter is not an expression formed by the operations of addition and multiplication defined above (from which only finite sums can be constructed). This notational convention allows reformulation the above definitions as
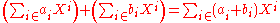
and
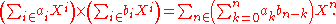
which is quite convenient, but one must be aware of the distinction between formal summation (a mere convention) and actual addition.

one would like to also give a meaning to the right hand side as an infinite summation. For that, one needs a notion of convergence in RN, in other words one must introduce a topology
on RN. There are several equivalent ways to define the appropriate topology.
Informally, two sequences (an) and (bn) become closer and closer if (and only if!) more and more of their terms agree exactly. Formally, the sequence of partial sums of some infinite summation converges if for every fixed power of X the coefficient stabilizes: there is a point beyond which all further partial sums have the same coefficient. This is clearly the case for the right hand side of (1), regardless of the values an, since inclusion of the term for i = n gives the last (and in fact only) change to the coefficient of Xn. It is also obvious that the limit
of the sequence of partial sums is equal to the left hand side.
This topological structure, together with the ring operations described above, form a topological ring
. This is called the ring of formal power series over R and is denoted by R
The topological structure allows much more flexible use of infinite summations. For instance the rule for multiplication can be restated simply as
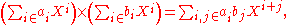
since only finitely many terms on the right affect any fixed Xn. Infinite products are also defined by the topological structure; it can be seen that an infinite product converges if and only if the sequence of its factors converges to 1.
for which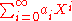 always converges as a summation to the formal power series designated by the same expression, and it often suffices to give a meaning to infinite sums and products, or other kinds of limits that one wishes to use to designate particular formal power series. It can however happen occasionally that one wishes to use a coarser topology, so that certain expressions become convergent that would otherwise diverge. This applies in particular when the base ring R already comes with a topology other than the discrete one, for instance if it is also a ring of formal power series.
always converges as a summation to the formal power series designated by the same expression, and it often suffices to give a meaning to infinite sums and products, or other kinds of limits that one wishes to use to designate particular formal power series. It can however happen occasionally that one wishes to use a coarser topology, so that certain expressions become convergent that would otherwise diverge. This applies in particular when the base ring R already comes with a topology other than the discrete one, for instance if it is also a ring of formal power series.
Consider the ring of formal power series

then the topology of above construction only relates to the indeterminate Y, since the topology that was put on has been replaced by the discrete topology when defining the topology of the whole ring. So
has been replaced by the discrete topology when defining the topology of the whole ring. So
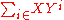
converges to the power series suggested, which can be written as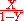 ; however the summation
; however the summation
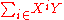
would be considered to be divergent, since every term affects the coefficient of Y (which coefficient is itself a power series in X). This asymmetry disappears if the power series ring in Y is given the product topology where each copy of is given its topology as a ring of formal power series rather than the discrete topology. As a consequence, for convergence of a sequence of elements of
is given its topology as a ring of formal power series rather than the discrete topology. As a consequence, for convergence of a sequence of elements of 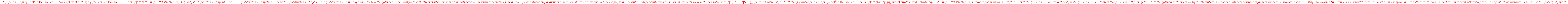 it then suffices that the coefficient of each power of Y converges to a formal power series in X, a weaker condition that stabilizing entirely; for instance in the second example given here the coefficient of Y converges to
it then suffices that the coefficient of each power of Y converges to a formal power series in X, a weaker condition that stabilizing entirely; for instance in the second example given here the coefficient of Y converges to  , so the whole summation converges to
, so the whole summation converges to  .
.
This way of defining the topology is in fact the standard one for repeated constructions of rings of formal power series, and gives the same topology as one would get by taking formal power series in all inderteminates at once. In the above example that would mean constructing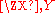 , and here a sequence converges if and only if the coefficient of every monomial XiYj stabilizes. This topology, which is also the I-adic topology, where I = (X,Y) is the ideal generated by X and Y, still enjoys the property that a summation converges if and only if its terms tend to 0.
, and here a sequence converges if and only if the coefficient of every monomial XiYj stabilizes. This topology, which is also the I-adic topology, where I = (X,Y) is the ideal generated by X and Y, still enjoys the property that a summation converges if and only if its terms tend to 0.
The same principle could be used to make other divergent limits converge. For instance in the limit
the limit
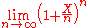
does not exist, so in particular it does not converge to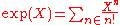 . This is because for i≥2 the coefficient
. This is because for i≥2 the coefficient  of Xidoes not stabilize as n goes to infinity. It does however converge in the usual topology of R, and in fact to the coefficient
of Xidoes not stabilize as n goes to infinity. It does however converge in the usual topology of R, and in fact to the coefficient  of exp(X). Therefore, if one would give
of exp(X). Therefore, if one would give  the product topology of RN where the topology of R is the usual topology rather than the discrete one, then the above limit would converge to exp(X). This more permissive approach is not however the standard when considering formal power series, as it would lead to convergence considerations that are as subtle as they are in analysis, while the philosophy of formal power series is on the contrary to make convergence questions as trivial as they can possibly be. With this topology it would not be the case that a summation converges if and only if its terms tend to 0.
the product topology of RN where the topology of R is the usual topology rather than the discrete one, then the above limit would converge to exp(X). This more permissive approach is not however the standard when considering formal power series, as it would lead to convergence considerations that are as subtle as they are in analysis, while the philosophy of formal power series is on the contrary to make convergence questions as trivial as they can possibly be. With this topology it would not be the case that a summation converges if and only if its terms tend to 0.
. If S is a commutative associative algebra over R, if I is an ideal of S such that the I-adic topology on S is complete, and if x is an element of I, then there is a unique Φ : R
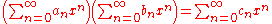
where
The sequence is the Cauchy product of the sequences
is the Cauchy product of the sequences 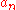 and
and 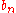 .
.
we have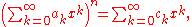
where
for . (This formula can only be used if
. (This formula can only be used if  and
and  are invertible in the ring of scalars.)
are invertible in the ring of scalars.)
In the case of formal power series with complex coefficients, the complex powers are well defined at least for series with constant term equal to
with constant term equal to  . In this case,
. In this case,  can be defined either by composition with the binomial series
can be defined either by composition with the binomial series
 , or by composition with the exponential and the logarithmic series,
, or by composition with the exponential and the logarithmic series, 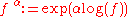 , or as the solution of the differential equation
, or as the solution of the differential equation  with constant term
with constant term 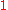 , the three definitions being equivalent. The rules of calculus
, the three definitions being equivalent. The rules of calculus  and
and 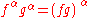 easily follow.
easily follow.
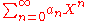
in R
This is necessary, as the constant term
of the product is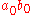 ,
,
and sufficient, via the explicit formula: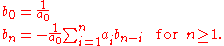
An important special case is that the geometric series formula is valid in R

If R=K is a field, then a series is invertible if and only if the constant term is non-zero, i.e., if and only if it is not divisible by X. This says that is a discrete valuation ring
is a discrete valuation ring
with uniformizing parameter X.
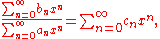
assuming the denominator is invertible (that is, is invertible in the ring of scalars), can be performed as a product f and the inverse of g, or directly equating the coefficients in f = gh:
is invertible in the ring of scalars), can be performed as a product f and the inverse of g, or directly equating the coefficients in f = gh:
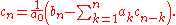

in is written
is written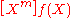
and extracts the coefficient of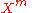 , so that
, so that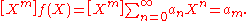
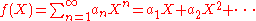
and
one may form the composition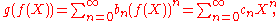
where the coefficients cn are determined by "expanding out" the powers of f(X):
Here the sum is extended over all (k,j) with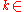 and
and 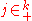 with
with 
A more explicit description of these coefficients is provided by Faà di Bruno's formula, at least in the case where the coefficient ring is a field of characteristic 0
.
A point here is that this operation is only valid when f(X) has no constant term, so that the series for g(f(X)) converges in the topology of R
If we denote by exp(X) the formal power series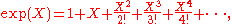
then the expression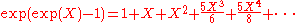
makes perfect sense as a formal power series. However, the statement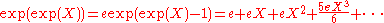
is not a valid application of the composition operation for formal power series. Rather, it is confusing the notions of convergence in R
 with
with  has a composition inverse
has a composition inverse 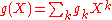 provided
provided  is an invertible element of R. The coefficients are found recursively from the above formula for the coefficients of a composition, equating them with those of the composition identity X (that is 1 at degree 1 and 0 at every degree greater than 1) . In the case when the coefficient ring is a field of characteristic 0, the Lagrange inversion formula provides a powerful tool to compute the coefficients of g, as well as the coefficients of the (multiplicative) powers of g.
is an invertible element of R. The coefficients are found recursively from the above formula for the coefficients of a composition, equating them with those of the composition identity X (that is 1 at degree 1 and 0 at every degree greater than 1) . In the case when the coefficient ring is a field of characteristic 0, the Lagrange inversion formula provides a powerful tool to compute the coefficients of g, as well as the coefficients of the (multiplicative) powers of g.
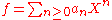
in R
, denoted Df or , by
, by
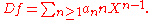
The symbol D is called the formal differentiation operator. The motivation behind this definition is that it simply mimics term-by-term differentiation of a polynomial.
This operation is R-linear:

for any a, b in R and any f, g in R
of calculus. For example, the product rule
is valid:

and the chain rule
works as well:
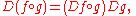
whenever the appropriate compositions of series are defined (see above under composition of series).
In a sense, all formal power series are Taylor series
. Indeed, for the f defined above, we find that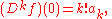
where Dk denotes the kth formal derivative (that is, the result of formally differentiating k times).
over R which contains the ring R[X] of polynomials over R; the polynomials correspond to the sequences which end in zeros.
The Jacobson radical
of R
generated by X and the Jacobson radical of R; this is implied by the element invertibility criterion discussed above.
The maximal ideal
s of R
Several algebraic properties of R are inherited by R
The ring R
if and only if R is finite. This follows from Tychonoff's theorem
and the characterisation of the topology on R
s, see the article on Examples of generating functions
.
One can use formal power series to prove several relations familiar from analysis in a purely algebraic setting. Consider for instance the following elements of Q
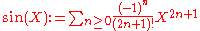

Then one can show that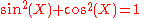
and

as well as

(the latter being valid in the ring Q
In algebra, the ring K
, every convergent power series defines a function
with values in the real
or complex
numbers. Formal power series can also be interpreted as functions, but one has to be careful with the domain and codomain
. If f = ∑an Xn is an element of R

This latter series is guaranteed to converge in S given the above assumptions on x. Furthermore, we have
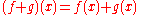
and
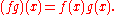
Unlike in the case of bona fide functions, these formulas are not definitions but have to be proved.
Since the topology on R
(so that they belong to the ideal (X)): f(0), f(X2−X) and f( (1 − X)−1 − 1) are all well defined for any formal power series f∈R
With this formalism, we can give an explicit formula for the multiplicative inverse of a power series f whose constant coefficient a = f(0) is invertible in R:
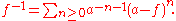
If the formal power series g with g(0) = 0 is given implicitly by the equation

where f is a known power series with f(0) = 0, then the coefficients of g can be explicitly computed using the Lagrange inversion formula.
), that is series of the form
where for all but finitely many negative indices n. Multiplication of such series can be defined. Indeed, similarly to the definition for formal power series, the coefficient of
for all but finitely many negative indices n. Multiplication of such series can be defined. Indeed, similarly to the definition for formal power series, the coefficient of 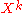 of two series with respective sequences of coefficients
of two series with respective sequences of coefficients 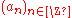 and
and  is
is
which sum is effectively finite because of the assumed vanishing of coefficients at sufficiently negative indices, and which sum zero for sufficiently negative k for the same reason.
For a non-zero formal Laurent series, the minimal integer n such that an≠0 is called the order of f, denoted ord(f). (The order of the zero series is +∞.) The formal Laurent series form the ring of formal Laurent series over R, denoted by R((X)). It is equal to the localization
of R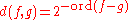 .
.
If R = K is a field
, then K((X)) is in fact a field, which may alternatively be obtained as the field of fractions
of the integral domain K
One may define formal differentiation for formal Laurent series in a natural way (term-by-term). Precisely, the formal derivative of the formal Laurent series f above is
which is again an element of K((X)). Notice that if f is a non-constant formal Laurent series, and K is a field of characteristic 0, then one has
However, in general this is not the case since the factor n for the lowest order term could be equal to 0 in R.
0. Then the map

is a K-derivation
that verifies

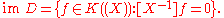
The latter shows that the coefficient of X−1 in ƒ is of particular interest; it is called formal residue of ƒ and denoted Res(ƒ). The map
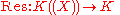
is K-linear, and by the above observation one has an exact sequence
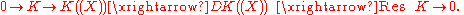
Some rules of calculus. As a quite direct consequence of the above definition, and of the rules of formal derivation, one has, for any ƒ and g in K((X))
Property (i) is part of the exact sequence above. Property (ii) follows from (i) as applied to (ƒg)' = ƒg' + ƒ'g. Property (iii): any ƒ can be written in the form ƒ = xm g, with m = ord(ƒ) and ord(g) = 0: then ƒ'/ƒ = mX −1 + g'/g. Since ord(g) = 0, the element g is invertible in K g) g' = f−1 g−1 g' + (F'
g) g' = f−1 g−1 g' + (F'  g) g' = ƒ−1 g'/g + (F
g) g' = ƒ−1 g'/g + (F  g)' and (iv) follows from (i) and (iii). Property (v) is clear from the definition.
g)' and (iv) follows from (i) and (iii). Property (v) is clear from the definition.
 with
with  and
and  has a composition inverse
has a composition inverse  . The following relation between the coefficients of
. The following relation between the coefficients of  and
and 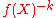 holds (""):
holds (""):
In particular, for n = 1 and all k ≥ 1,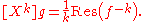
Since the proof of the Lagrange inversion formula is a very short computation, it is worth reporting it here. By the above rules of calculus,

Generalizations. One may observe that the above computation can be repeated plainly in more general settings than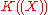 : a generalization of the Lagrange inversion formula is already available working in the
: a generalization of the Lagrange inversion formula is already available working in the  -modules
-modules 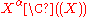 , where
, where  is a complex exponent. As a consequence, if f and g are as above, with
is a complex exponent. As a consequence, if f and g are as above, with 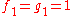 , we can relate the complex powers of f/X and g/X: precisely, if
, we can relate the complex powers of f/X and g/X: precisely, if  and
and  are non-zero complex numbers with negative integer sum,
are non-zero complex numbers with negative integer sum, 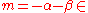 , then
, then
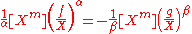 .
.
For instance, this way one finds the power series for complex powers of the Lambert function.
Xα is any finite product of elements of XI (repetitions allowed); a formal power series in XI with coefficients in a ring R is determined by any mapping from the set of monomials Xα to a corresponding coefficient cα, and is denoted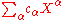 . The set of all such formal power series is denoted R
. The set of all such formal power series is denoted R
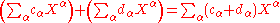
and
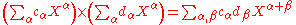
As remarked above, the topology on a repeated formal power series ring like R
to R
In the case of the formal derivative, there are now separate partial derivative
operators, which differentiate with respect to each of the indeterminates. They all commute with each other.
Suppose G is an ordered abelian group, meaning an abelian group with a total ordering "<" respecting the group's addition, so that a < b if and only if a + c < b + c for all c. Let I be a well-ordered subset of G, meaning I contains no infinite descending chain. Consider the set consisting of
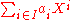
for all such I, with ai in a commutative ring R, where we assume that for any index set, if all of the ai are zero then the sum is zero. Then R((G)) is the ring of formal power series on G; because of the condition that the indexing set be well-ordered the product is well-defined, and we of course assume that two elements which differ by zero are the same.
Various properties of R transfer to R((G)). If R is a field, then so is R((G)). If R is an ordered field, we can order R((G)) by setting any element to have the same sign as its leading coefficient, defined as the least element of the index set I associated to a non-zero coefficient. Finally if G is a divisible group
and R is a real closed field
, then R((G)) is a real closed field, and if R is algebraically closed, then so is R((G)).
This theory is due to Hans Hahn
, who also showed that one obtains subfields when the number of (non-zero) terms is bounded by some fixed infinite cardinality.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates. This perspective contrasts with that of power series, whose variables designate numerical values, and which series therefore only have a definite value if convergence can be established. Formal power series are often used merely to represent the whole collection of their coefficients. In combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
they provide representations of numerical sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s and of multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s, and for instance allow giving concise expressions for recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
defined sequences regardless of whether the recursion can be explicitly solved; this is known as the method of generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s.
Introduction
A formal power series can be loosely thought of as an object that is like a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, but with infinitely many terms. Alternatively, for those familiar with power series (or Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
), one may think of a formal power series as a power series in which we ignore questions of convergence
Convergence (series)
Convergence is a series of books edited by Ruth Nanda Anshen and published by the Columbia University Press dealing with ideas that changed, or that are changing the world....
by not assuming that x denotes any numerical value (not even an unknown value). For example, consider the series

If we studied this as a power series, its properties would include, for example, that its radius of convergence is 1. However, as a formal power series, we may ignore this completely; all that is relevant is the sequence of coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s [1, −3, 5, −7, 9, −11, ...]. In other words, a formal power series is an object that just records a sequence of coefficients. It is perfectly acceptable to consider a formal power series with as coefficients [1, 1, 2, 6 , 24, 120, 720, 5040, … ] (the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s), even though the corresponding power series diverges for any nonzero value of x.
Arithmetic on formal power series is carried out by simply pretending that the series are polynomials. For example, if

then we add A and B term by term:

We can multiply formal power series, again just by treating them as polynomials (see in particular Cauchy product):

Notice that each coefficient in the product AB only depends on a finite number of coefficients of A and B. For example, the x5 term is given by
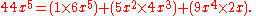
For this reason, one may multiply formal power series without worrying about the usual questions of absolute
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, conditional and uniform convergence which arise in dealing with power series in the setting of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Once we have defined multiplication for formal power series, we can define multiplicative inverses as follows. The multiplicative inverse of a formal power series A is a formal power series C such that AC = 1, provided that such a formal power series exists. It turns out that if A has a multiplicative inverse, it is unique, and we denote it by A −1. Now we can define division of formal power series by defining B / A to be the product B A −1, provided that the inverse of A exists. For example, one can use the definition of multiplication above to verify the familiar formula
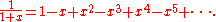
An important operation on formal power series is coefficient extraction. In its most basic form, the coefficient extraction operator for a formal power series in one variable extracts the coefficient of xn, and is written e.g. [xn] A, so that [x2] A = 5 and [x5] A = −11. Other examples include
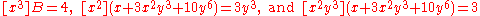
and

Similarly, many other operations that are carried out on polynomials can be extended to the formal power series setting, as explained below.
The ring of formal power series
The set of all formal power series in X with coefficients in a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R form another ring that is written R
Definition of the formal power series ring
One can characterize RPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
ring R[X] equipped with a particular metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. This automatically gives R
It is possible to describe R
Ring structure
As a set, RNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (taken to include 0). Designating a sequence whose term at index n is an by
 , one defines addition of two such sequences by
, one defines addition of two such sequences by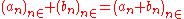
and multiplication by
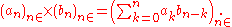
This type of product is called the Cauchy product of the two sequences of coefficients, and is a sort of discrete convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. With these operations, RN becomes a commutative ring with zero element (0, 0, 0, ...) and multiplicative identity (1, 0, 0,...).
The product is in fact the same one used to define the product of polynomials in one indeterminate, which suggests using a similar notation. One embeds R into R
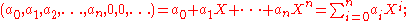
these are precisely the polynomials in X. Given this, it is quite natural and convenient to designate a general sequence an by
 by the formal expression
by the formal expression 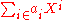 , even though the latter is not an expression formed by the operations of addition and multiplication defined above (from which only finite sums can be constructed). This notational convention allows reformulation the above definitions as
, even though the latter is not an expression formed by the operations of addition and multiplication defined above (from which only finite sums can be constructed). This notational convention allows reformulation the above definitions as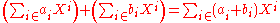
and
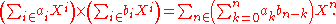
which is quite convenient, but one must be aware of the distinction between formal summation (a mere convention) and actual addition.
Topological structure
Having decreed as a convention that
one would like to also give a meaning to the right hand side as an infinite summation. For that, one needs a notion of convergence in RN, in other words one must introduce a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on RN. There are several equivalent ways to define the appropriate topology.
- We may give RN the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, where each copy of R is given the discrete topology. - We may give RN the I-adic topology, where I = (X) is the ideal generated by X, which consists of all sequences whose first term a0 is zero.
- For those not acquainted with general topology, the desired topology can also be derived from the following metricMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(or "distance function"). The distance between distinct sequences (an) and (bn) in RN, is defined to be
-
- where k is the smallest natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
such that ak ≠ bk; the distance between two equal sequences is of course zero.
Informally, two sequences (an) and (bn) become closer and closer if (and only if!) more and more of their terms agree exactly. Formally, the sequence of partial sums of some infinite summation converges if for every fixed power of X the coefficient stabilizes: there is a point beyond which all further partial sums have the same coefficient. This is clearly the case for the right hand side of (1), regardless of the values an, since inclusion of the term for i = n gives the last (and in fact only) change to the coefficient of Xn. It is also obvious that the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of the sequence of partial sums is equal to the left hand side.
This topological structure, together with the ring operations described above, form a topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
. This is called the ring of formal power series over R and is denoted by R
The topological structure allows much more flexible use of infinite summations. For instance the rule for multiplication can be restated simply as
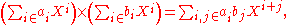
since only finitely many terms on the right affect any fixed Xn. Infinite products are also defined by the topological structure; it can be seen that an infinite product converges if and only if the sequence of its factors converges to 1.
Alternative topologies
The above topology is the finest topologyComparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
for which
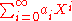 always converges as a summation to the formal power series designated by the same expression, and it often suffices to give a meaning to infinite sums and products, or other kinds of limits that one wishes to use to designate particular formal power series. It can however happen occasionally that one wishes to use a coarser topology, so that certain expressions become convergent that would otherwise diverge. This applies in particular when the base ring R already comes with a topology other than the discrete one, for instance if it is also a ring of formal power series.
always converges as a summation to the formal power series designated by the same expression, and it often suffices to give a meaning to infinite sums and products, or other kinds of limits that one wishes to use to designate particular formal power series. It can however happen occasionally that one wishes to use a coarser topology, so that certain expressions become convergent that would otherwise diverge. This applies in particular when the base ring R already comes with a topology other than the discrete one, for instance if it is also a ring of formal power series.Consider the ring of formal power series

then the topology of above construction only relates to the indeterminate Y, since the topology that was put on
 has been replaced by the discrete topology when defining the topology of the whole ring. So
has been replaced by the discrete topology when defining the topology of the whole ring. So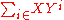
converges to the power series suggested, which can be written as
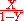 ; however the summation
; however the summation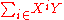
would be considered to be divergent, since every term affects the coefficient of Y (which coefficient is itself a power series in X). This asymmetry disappears if the power series ring in Y is given the product topology where each copy of
 is given its topology as a ring of formal power series rather than the discrete topology. As a consequence, for convergence of a sequence of elements of
is given its topology as a ring of formal power series rather than the discrete topology. As a consequence, for convergence of a sequence of elements of 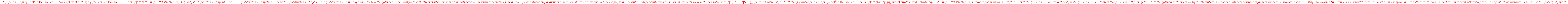 it then suffices that the coefficient of each power of Y converges to a formal power series in X, a weaker condition that stabilizing entirely; for instance in the second example given here the coefficient of Y converges to
it then suffices that the coefficient of each power of Y converges to a formal power series in X, a weaker condition that stabilizing entirely; for instance in the second example given here the coefficient of Y converges to  , so the whole summation converges to
, so the whole summation converges to  .
.This way of defining the topology is in fact the standard one for repeated constructions of rings of formal power series, and gives the same topology as one would get by taking formal power series in all inderteminates at once. In the above example that would mean constructing
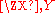 , and here a sequence converges if and only if the coefficient of every monomial XiYj stabilizes. This topology, which is also the I-adic topology, where I = (X,Y) is the ideal generated by X and Y, still enjoys the property that a summation converges if and only if its terms tend to 0.
, and here a sequence converges if and only if the coefficient of every monomial XiYj stabilizes. This topology, which is also the I-adic topology, where I = (X,Y) is the ideal generated by X and Y, still enjoys the property that a summation converges if and only if its terms tend to 0.The same principle could be used to make other divergent limits converge. For instance in
 the limit
the limit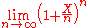
does not exist, so in particular it does not converge to
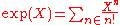 . This is because for i≥2 the coefficient
. This is because for i≥2 the coefficient  of Xidoes not stabilize as n goes to infinity. It does however converge in the usual topology of R, and in fact to the coefficient
of Xidoes not stabilize as n goes to infinity. It does however converge in the usual topology of R, and in fact to the coefficient  of exp(X). Therefore, if one would give
of exp(X). Therefore, if one would give  the product topology of RN where the topology of R is the usual topology rather than the discrete one, then the above limit would converge to exp(X). This more permissive approach is not however the standard when considering formal power series, as it would lead to convergence considerations that are as subtle as they are in analysis, while the philosophy of formal power series is on the contrary to make convergence questions as trivial as they can possibly be. With this topology it would not be the case that a summation converges if and only if its terms tend to 0.
the product topology of RN where the topology of R is the usual topology rather than the discrete one, then the above limit would converge to exp(X). This more permissive approach is not however the standard when considering formal power series, as it would lead to convergence considerations that are as subtle as they are in analysis, while the philosophy of formal power series is on the contrary to make convergence questions as trivial as they can possibly be. With this topology it would not be the case that a summation converges if and only if its terms tend to 0.Universal property
The ring RUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. If S is a commutative associative algebra over R, if I is an ideal of S such that the I-adic topology on S is complete, and if x is an element of I, then there is a unique Φ : R
- Φ is an R-algebra homomorphism
- Φ is continuous
- Φ(X) = x.
Operations on formal power series
One can perform algebraic operations on power series to generate new power series.Multiplying series
The product of two series is given by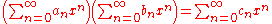
where

The sequence
 is the Cauchy product of the sequences
is the Cauchy product of the sequences 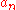 and
and 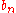 .
.Power series raised to powers
If n is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
we have
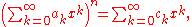
where

for
 . (This formula can only be used if
. (This formula can only be used if  and
and  are invertible in the ring of scalars.)
are invertible in the ring of scalars.)In the case of formal power series with complex coefficients, the complex powers are well defined at least for series
 with constant term equal to
with constant term equal to  . In this case,
. In this case,  can be defined either by composition with the binomial series
can be defined either by composition with the binomial seriesBinomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
 , or by composition with the exponential and the logarithmic series,
, or by composition with the exponential and the logarithmic series, 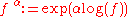 , or as the solution of the differential equation
, or as the solution of the differential equation  with constant term
with constant term 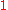 , the three definitions being equivalent. The rules of calculus
, the three definitions being equivalent. The rules of calculus  and
and 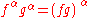 easily follow.
easily follow.Inverting series
The series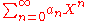
in R
This is necessary, as the constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
of the product is
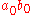 ,
,and sufficient, via the explicit formula:
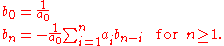
An important special case is that the geometric series formula is valid in R

If R=K is a field, then a series is invertible if and only if the constant term is non-zero, i.e., if and only if it is not divisible by X. This says that
 is a discrete valuation ring
is a discrete valuation ringDiscrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
with uniformizing parameter X.
Dividing series
The computation of a quotient f/g = h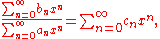
assuming the denominator is invertible (that is,
 is invertible in the ring of scalars), can be performed as a product f and the inverse of g, or directly equating the coefficients in f = gh:
is invertible in the ring of scalars), can be performed as a product f and the inverse of g, or directly equating the coefficients in f = gh: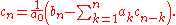
Extracting coefficients
The coefficient extraction operator applied to a formal power series
in
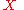 is written
is written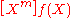
and extracts the coefficient of
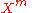 , so that
, so that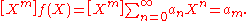
Composition of series
Given formal power series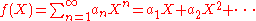
and

one may form the composition
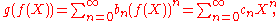
where the coefficients cn are determined by "expanding out" the powers of f(X):

Here the sum is extended over all (k,j) with
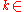 and
and 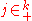 with
with 
A more explicit description of these coefficients is provided by Faà di Bruno's formula, at least in the case where the coefficient ring is a field of characteristic 0
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
.
A point here is that this operation is only valid when f(X) has no constant term, so that the series for g(f(X)) converges in the topology of R
Example
(We assume in this example that the ring R has characteristic 0.)If we denote by exp(X) the formal power series
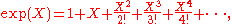
then the expression
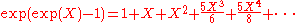
makes perfect sense as a formal power series. However, the statement
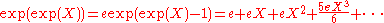
is not a valid application of the composition operation for formal power series. Rather, it is confusing the notions of convergence in R
Composition inverse
Any formal series with
with  has a composition inverse
has a composition inverse 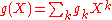 provided
provided 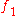 is an invertible element of R. The coefficients are found recursively from the above formula for the coefficients of a composition, equating them with those of the composition identity X (that is 1 at degree 1 and 0 at every degree greater than 1) . In the case when the coefficient ring is a field of characteristic 0, the Lagrange inversion formula provides a powerful tool to compute the coefficients of g, as well as the coefficients of the (multiplicative) powers of g.
is an invertible element of R. The coefficients are found recursively from the above formula for the coefficients of a composition, equating them with those of the composition identity X (that is 1 at degree 1 and 0 at every degree greater than 1) . In the case when the coefficient ring is a field of characteristic 0, the Lagrange inversion formula provides a powerful tool to compute the coefficients of g, as well as the coefficients of the (multiplicative) powers of g.Formal differentiation of series
Given a formal power series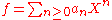
in R
Formal derivative
In mathematics, the formal derivative is an operation on elements of a polynomial ring or a ring of formal power series that mimics the form of the derivative from calculus. Though they appear similar, the algebraic advantage of a formal derivative is that it does not rely on the notion of a...
, denoted Df or
 , by
, by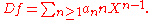
The symbol D is called the formal differentiation operator. The motivation behind this definition is that it simply mimics term-by-term differentiation of a polynomial.
This operation is R-linear:

for any a, b in R and any f, g in R
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of calculus. For example, the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
is valid:

and the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
works as well:
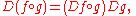
whenever the appropriate compositions of series are defined (see above under composition of series).
In a sense, all formal power series are Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. Indeed, for the f defined above, we find that
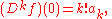
where Dk denotes the kth formal derivative (that is, the result of formally differentiating k times).
Algebraic properties of the formal power series ring
RAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over R which contains the ring R[X] of polynomials over R; the polynomials correspond to the sequences which end in zeros.
The Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of R
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by X and the Jacobson radical of R; this is implied by the element invertibility criterion discussed above.
The maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s of R
Several algebraic properties of R are inherited by R
- if R is a local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, then so is RX - if R is NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, then so is RX ; this is a version of the Hilbert basis theorem - if R is an integral domain, then so is R
X - if R = K is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then KX is a discrete valuation ring Discrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
.
Topological properties of the formal power series ring
The metric space (RThe ring R
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
if and only if R is finite. This follows from Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
and the characterisation of the topology on R
Applications
Formal power series can be used to solve recurrences occurring in number theory and combinatorics. For an example involving finding a closed form expression for the Fibonacci numberFibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, see the article on Examples of generating functions
Examples of generating functions
The following examples are in the spirit of George Pólya, who advocated learning mathematics by doing and re-capitulating as many examples and proofs as possible...
.
One can use formal power series to prove several relations familiar from analysis in a purely algebraic setting. Consider for instance the following elements of Q
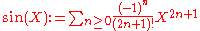

Then one can show that
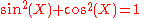
and

as well as

(the latter being valid in the ring Q
In algebra, the ring K
Interpreting formal power series as functions
In mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, every convergent power series defines a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with values in the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers. Formal power series can also be interpreted as functions, but one has to be careful with the domain and codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. If f = ∑an Xn is an element of R

This latter series is guaranteed to converge in S given the above assumptions on x. Furthermore, we have
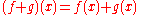
and
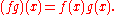
Unlike in the case of bona fide functions, these formulas are not definitions but have to be proved.
Since the topology on R
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
(so that they belong to the ideal (X)): f(0), f(X2−X) and f( (1 − X)−1 − 1) are all well defined for any formal power series f∈R
With this formalism, we can give an explicit formula for the multiplicative inverse of a power series f whose constant coefficient a = f(0) is invertible in R:
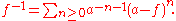
If the formal power series g with g(0) = 0 is given implicitly by the equation

where f is a known power series with f(0) = 0, then the coefficients of g can be explicitly computed using the Lagrange inversion formula.
Formal Laurent series
A formal Laurent series over a ring R is defined in a similar way to a formal power series, except that we also allow finitely many terms of negative degree (this is different from the classical Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
), that is series of the form

where
 for all but finitely many negative indices n. Multiplication of such series can be defined. Indeed, similarly to the definition for formal power series, the coefficient of
for all but finitely many negative indices n. Multiplication of such series can be defined. Indeed, similarly to the definition for formal power series, the coefficient of 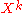 of two series with respective sequences of coefficients
of two series with respective sequences of coefficients 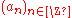 and
and  is
is
which sum is effectively finite because of the assumed vanishing of coefficients at sufficiently negative indices, and which sum zero for sufficiently negative k for the same reason.
For a non-zero formal Laurent series, the minimal integer n such that an≠0 is called the order of f, denoted ord(f). (The order of the zero series is +∞.) The formal Laurent series form the ring of formal Laurent series over R, denoted by R((X)). It is equal to the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of R
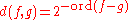 .
.If R = K is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then K((X)) is in fact a field, which may alternatively be obtained as the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the integral domain K
One may define formal differentiation for formal Laurent series in a natural way (term-by-term). Precisely, the formal derivative of the formal Laurent series f above is

which is again an element of K((X)). Notice that if f is a non-constant formal Laurent series, and K is a field of characteristic 0, then one has

However, in general this is not the case since the factor n for the lowest order term could be equal to 0 in R.
Formal residue
Assume that R is a field K of characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0. Then the map

is a K-derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
that verifies

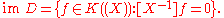
The latter shows that the coefficient of X−1 in ƒ is of particular interest; it is called formal residue of ƒ and denoted Res(ƒ). The map
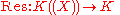
is K-linear, and by the above observation one has an exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
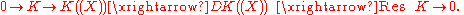
Some rules of calculus. As a quite direct consequence of the above definition, and of the rules of formal derivation, one has, for any ƒ and g in K((X))
- i.

- ii.
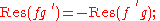
- iii.

- iv.

- v.

Property (i) is part of the exact sequence above. Property (ii) follows from (i) as applied to (ƒg)' = ƒg' + ƒ'g. Property (iii): any ƒ can be written in the form ƒ = xm g, with m = ord(ƒ) and ord(g) = 0: then ƒ'/ƒ = mX −1 + g'/g. Since ord(g) = 0, the element g is invertible in K
 g) g' = f−1 g−1 g' + (F'
g) g' = f−1 g−1 g' + (F'  g) g' = ƒ−1 g'/g + (F
g) g' = ƒ−1 g'/g + (F  g)' and (iv) follows from (i) and (iii). Property (v) is clear from the definition.
g)' and (iv) follows from (i) and (iii). Property (v) is clear from the definition.The Lagrange inversion formula
As mentioned above, any formal series with
with  and
and  has a composition inverse
has a composition inverse  . The following relation between the coefficients of
. The following relation between the coefficients of  and
and 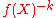 holds (""):
holds (""):
In particular, for n = 1 and all k ≥ 1,
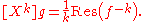
Since the proof of the Lagrange inversion formula is a very short computation, it is worth reporting it here. By the above rules of calculus,

Generalizations. One may observe that the above computation can be repeated plainly in more general settings than
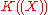 : a generalization of the Lagrange inversion formula is already available working in the
: a generalization of the Lagrange inversion formula is already available working in the  -modules
-modules 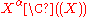 , where
, where  is a complex exponent. As a consequence, if f and g are as above, with
is a complex exponent. As a consequence, if f and g are as above, with 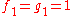 , we can relate the complex powers of f/X and g/X: precisely, if
, we can relate the complex powers of f/X and g/X: precisely, if  and
and  are non-zero complex numbers with negative integer sum,
are non-zero complex numbers with negative integer sum, 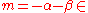 , then
, then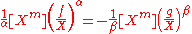 .
.For instance, this way one finds the power series for complex powers of the Lambert function.
Power series in several variables
Formal power series in any number of indeterminates (even infinitely many) can be defined. If I is an index set and XI is the set of indeterminates Xi for i∈I, then a monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
Xα is any finite product of elements of XI (repetitions allowed); a formal power series in XI with coefficients in a ring R is determined by any mapping from the set of monomials Xα to a corresponding coefficient cα, and is denoted
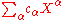 . The set of all such formal power series is denoted R
. The set of all such formal power series is denoted R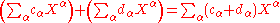
and
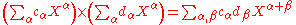
Topology
The topology on RAs remarked above, the topology on a repeated formal power series ring like R
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
to R
Operations
All of the operations defined for series in one variable may be extended to the several variables case.- A series is invertible if and only if its constant term is invertible in R.
- The composition f(g(X)) of two series f and g is defined if f is a series in a single indeterminate, and the constant term of g is zero. For a series f in several indeterminates a form of "composition" can similarly be defined, with as many separate series in the place of g as there are indeterminates.
In the case of the formal derivative, there are now separate partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
operators, which differentiate with respect to each of the indeterminates. They all commute with each other.
Universal property
In the several variables case, the universal property characterizing R- Φ is an R-algebra homomorphism
- Φ is continuous
- Φ(Xi) = xi for i = 1, ..., r.
Replacing the index set by an ordered abelian group
- (Main article: Hahn seriesHahn seriesIn mathematics, Hahn series are a type of formal infinite series. They are a generalization of Puiseux series and were first introduced by Hans Hahn in 1907...
)
Suppose G is an ordered abelian group, meaning an abelian group with a total ordering "<" respecting the group's addition, so that a < b if and only if a + c < b + c for all c. Let I be a well-ordered subset of G, meaning I contains no infinite descending chain. Consider the set consisting of
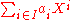
for all such I, with ai in a commutative ring R, where we assume that for any index set, if all of the ai are zero then the sum is zero. Then R((G)) is the ring of formal power series on G; because of the condition that the indexing set be well-ordered the product is well-defined, and we of course assume that two elements which differ by zero are the same.
Various properties of R transfer to R((G)). If R is a field, then so is R((G)). If R is an ordered field, we can order R((G)) by setting any element to have the same sign as its leading coefficient, defined as the least element of the index set I associated to a non-zero coefficient. Finally if G is a divisible group
Divisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
and R is a real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
, then R((G)) is a real closed field, and if R is algebraically closed, then so is R((G)).
This theory is due to Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
, who also showed that one obtains subfields when the number of (non-zero) terms is bounded by some fixed infinite cardinality.
Examples and related topics
- Bell seriesBell seriesIn mathematics, the Bell series is a formal power series used to study properties of arithmetical functions. Bell series were introduced and developed by Eric Temple Bell....
are used to study the properties of multiplicative arithmetic functionsMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...