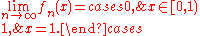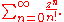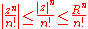
Uniform convergence
Encyclopedia
In the mathematical
field of analysis
, uniform convergence is a type of convergence
stronger than pointwise convergence
. A sequence
{fn} of functions
converges uniformly to a limiting function f if the speed of convergence of fn(x) to f(x) does not depend on x.
The concept is important because several properties of the functions fn, such as continuity
and Riemann integrability
, are transferred to the limit
f if the convergence is uniform.
in 1821 published a false statement, but with a purported proof, that the pointwise limit of a sequence of continuous functions is always continuous; however, Lakatos offers a re-assessment of Cauchy's approach. Niels Henrik Abel
in 1826 found purported counterexamples to this statement in the context of Fourier series
, arguing that Cauchy's proof had to be incorrect. Cauchy ultimately responded in 1853 with a clarification of his 1821 formulation.
The term uniform convergence was probably first used by Christoph Gudermann
, in an 1838 paper on elliptic functions, where he employed the phrase "convergence in a uniform way" when the "mode of convergence" of a series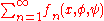
is independent of the variables 
and 
While he thought it a "remarkable fact" when a series converged in this way, he did not give a formal definition, nor use the property in any of his proofs.
Later Gudermann's pupil Karl Weierstrass
, who attended his course on elliptic functions in 1839–1840, coined the term gleichmäßig konvergent which he used in his 1841 paper Zur Theorie der Potenzreihen, published in 1894. Independently a similar concept was used by Philipp Ludwig von Seidel
and George Gabriel Stokes
but without having any major impact on further development. G. H. Hardy
compares the three definitions in his paper Sir George Stokes and the concept of uniform convergence and remarks: Weierstrass's discovery was the earliest, and he alone fully realized its far-reaching importance as one of the fundamental ideas of analysis.
Under the influence of Weierstrass and Bernhard Riemann
this concept and related questions were intensely studied at the end of the 19th century by Hermann Hankel
, Paul du Bois-Reymond, Ulisse Dini, Cesare Arzelà
and others.
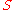is a set and is a real
-valued function for every natural number
. We say that the sequence is uniformly convergent with limit if for every , there exists a natural number such that for all and all we have .
Consider the sequence where the supremum
is taken over all . Clearly converges to uniformly if and only if
tends to 0.
The sequence is said to be locally uniformly convergent with limit if for every in some metric space , there exists an such that converges uniformly on .
, by replacing |fn(x) − f(x)| with d(fn(x), f(x)).
The most general setting is the uniform convergence of net
s of functions S → X, where X is a uniform space
. We say that the net (fα) converges uniformly with limit f : S → X if and only if
The above mentioned theorem, stating that the uniform limit of continuous functions is continuous, remains correct in these settings.
X, we can equip the space of bounded
real
or complex
-valued functions over X with the uniform norm topology. Then uniform convergence simply means convergence
in the uniform norm topology.
The sequence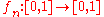
with 
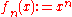converges pointwise but not uniformly:
In this example one can easily see that pointwise convergence does not preserve differentiability or continuity. While each function of the sequence is smooth, that is to say that for all n,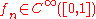
, the limit 
is not even continuous.
can be shown to be uniformly convergent on any bounded subset S of
using the Weierstrass M-test.
Here is the series:
Any bounded subset is a subset of some disc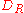
of radius R, centered on the origin in the complex plane
. The Weierstrass M-test requires us to find an upper bound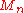
on the terms of the series, with 
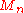independent of the position in the disc:
This is trivial:
If
is convergent, then the M-test asserts that the original series is uniformly convergent.
The ratio test can be used here:
which means the series over
is convergent.
Thus the original series converges uniformly for all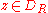
, and since 
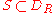, the series is also uniformly convergent on S.
If 
is a real interval
(or indeed any topological space
), we can talk about the continuity of the functions
and 
. The following is the more important result about uniform convergence:
This theorem is proved by the "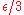
trick", and is the archetypal example of this trick: to prove a given inequality (
), one uses the definitions of continuity and uniform convergence to produce 3 inequalities (
), and then combines them via the triangle inequality
to produce the desired inequality.
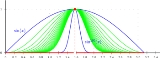
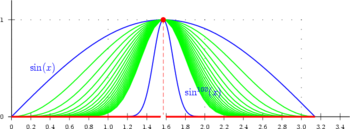
This theorem is important, since pointwise convergence of continuous functions is not enough to guarantee continuity of the limit function as the image illustrates.
More precisely, this theorem states that the uniform limit of uniformly continuous functions is uniformly continuous; for a locally compact space, continuity is equivalent to local uniform continuity, and thus the uniform limit of continuous functions is continuous.
is an interval and all the functions 
are differentiable
and converge to a limit
, it is often desirable to differentiate the limit function 
by taking the limit of the derivatives of 
. This is however in general not possible: even if the convergence is uniform, the limit function need not be differentiable, and even if it is differentiable, the derivative of the limit function need not be equal to the limit of the derivatives. Consider for instance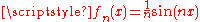 
with uniform limit 0, but the derivatives do not approach 0. The precise statement covering this situation is as follows:
, this can be done if uniform convergence is assumed:
Much stronger theorems in this respect, which require not much more than pointwise convergence, can be obtained if one abandons the Riemann integral and uses the Lebesgue integral
instead.
Note that almost uniform convergence of a sequence does not mean that the sequence converges uniformly almost everywhere
as might be inferred from the name.
Egorov's theorem
guarantees that on a finite measure space, a sequence of functions that converges almost everywhere also converges almost uniformly on the same set.
Almost uniform convergence implies almost everywhere convergence and convergence in measure
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, uniform convergence is a type of convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
stronger than pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. A sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
{fn} of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
converges uniformly to a limiting function f if the speed of convergence of fn(x) to f(x) does not depend on x.
The concept is important because several properties of the functions fn, such as continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and Riemann integrability
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, are transferred to the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
f if the convergence is uniform.
History
Some historians claim that Augustin Louis CauchyAugustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
in 1821 published a false statement, but with a purported proof, that the pointwise limit of a sequence of continuous functions is always continuous; however, Lakatos offers a re-assessment of Cauchy's approach. Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
in 1826 found purported counterexamples to this statement in the context of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, arguing that Cauchy's proof had to be incorrect. Cauchy ultimately responded in 1853 with a clarification of his 1821 formulation.
The term uniform convergence was probably first used by Christoph Gudermann
Christoph Gudermann
Christoph Gudermann was born in Vienenburg. He was the son of a school teacher and became a teacher himself after studying at the University of Göttingen, where his advisor was Karl Friedrich Gauss...
, in an 1838 paper on elliptic functions, where he employed the phrase "convergence in a uniform way" when the "mode of convergence" of a series
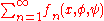is independent of the variables and While he thought it a "remarkable fact" when a series converged in this way, he did not give a formal definition, nor use the property in any of his proofs.Later Gudermann's pupil Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, who attended his course on elliptic functions in 1839–1840, coined the term gleichmäßig konvergent which he used in his 1841 paper Zur Theorie der Potenzreihen, published in 1894. Independently a similar concept was used by Philipp Ludwig von Seidel
Philipp Ludwig von Seidel
Philipp Ludwig von Seidel was a German mathematician. His mother was Julie Reinhold and his father was Justus Christian Felix Seidel.Lakatos credits von Seidel with discovering, in 1847, the crucial analytic concept of uniform convergence, while analyzing an incorrect proof of Cauchy's.In 1857,...
and George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
but without having any major impact on further development. G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
compares the three definitions in his paper Sir George Stokes and the concept of uniform convergence and remarks: Weierstrass's discovery was the earliest, and he alone fully realized its far-reaching importance as one of the fundamental ideas of analysis.
Under the influence of Weierstrass and Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
this concept and related questions were intensely studied at the end of the 19th century by Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
, Paul du Bois-Reymond, Ulisse Dini, Cesare Arzelà
Cesare Arzelà
Cesare Arzelà was an Italian mathematician who taught at the University of Bologna and is recognized for his contributions in the theory of functions, particularly for his characterization of sequences of continuous functions, generalizing the one given earlier by Giulio Ascoli in the famous...
and others.
Definition
Suppose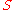 is a set and is a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function for every natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. We say that the sequence is uniformly convergent with limit if for every , there exists a natural number such that for all and all we have .Consider the sequence where the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over all . Clearly converges to uniformly if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
tends to 0.
The sequence is said to be locally uniformly convergent with limit if for every in some metric space , there exists an such that converges uniformly on .
Generalizations
One may straightforwardly extend the concept to functions S → M, where (M, d) is a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, by replacing |fn(x) − f(x)| with d(fn(x), f(x)).
The most general setting is the uniform convergence of net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
s of functions S → X, where X is a uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
. We say that the net (fα) converges uniformly with limit f : S → X if and only if
- for every entourage V in X, there exists an α0, such that for every x in I and every α ≥ α0: (fα(x), f(x)) is in V.
The above mentioned theorem, stating that the uniform limit of continuous functions is continuous, remains correct in these settings.
Examples
Given a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, we can equip the space of bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions over X with the uniform norm topology. Then uniform convergence simply means convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in the uniform norm topology.
The sequence
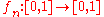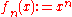with converges pointwise but not uniformly:
In this example one can easily see that pointwise convergence does not preserve differentiability or continuity. While each function of the sequence is smooth, that is to say that for all n,
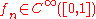, the limit is not even continuous.Exponential function
The series expansion of the exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
can be shown to be uniformly convergent on any bounded subset S of
using the Weierstrass M-test.Here is the series:
Any bounded subset is a subset of some disc
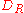of radius R, centered on the origin in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. The Weierstrass M-test requires us to find an upper bound
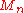on the terms of the series, with 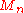independent of the position in the disc:
This is trivial:
If
is convergent, then the M-test asserts that the original series is uniformly convergent.The ratio test can be used here:
which means the series over
is convergent.Thus the original series converges uniformly for all
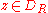, and since 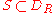, the series is also uniformly convergent on S.Properties
- Every uniformly convergent sequence is locally uniformly convergent.
- Every locally uniformly convergent sequence is compactly convergent.
- For locally compact spaceLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
s local uniform convergence and compact convergence coincide. - A sequence of continuous functions on metric spaces, with the image metric space being complete, is uniformly convergent if and only if it is uniformly Cauchy.
To continuity
is a real intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(or indeed any topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
), we can talk about the continuity of the functions
and . The following is the more important result about uniform convergence:
- Uniform convergence theorem. If
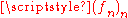is a sequence of continuous functions which converges uniformly towards the function 
on an interval 
, then 
is continuous on 
as well.
This theorem is proved by the "
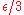trick", and is the archetypal example of this trick: to prove a given inequality (), one uses the definitions of continuity and uniform convergence to produce 3 inequalities (), and then combines them via the triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
to produce the desired inequality.
This theorem is important, since pointwise convergence of continuous functions is not enough to guarantee continuity of the limit function as the image illustrates.
More precisely, this theorem states that the uniform limit of uniformly continuous functions is uniformly continuous; for a locally compact space, continuity is equivalent to local uniform continuity, and thus the uniform limit of continuous functions is continuous.
To differentiability
If is an interval and all the functions are differentiableDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and converge to a limit
, it is often desirable to differentiate the limit function by taking the limit of the derivatives of . This is however in general not possible: even if the convergence is uniform, the limit function need not be differentiable, and even if it is differentiable, the derivative of the limit function need not be equal to the limit of the derivatives. Consider for instance 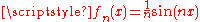with uniform limit 0, but the derivatives do not approach 0. The precise statement covering this situation is as follows:
- If
converges uniformly to 
, and if all the 
are differentiable, and if the derivatives 
converge uniformly to g, then 
is differentiable and its derivative is g.
To integrability
Similarly, one often wants to exchange integrals and limit processes. For the Riemann integralRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, this can be done if uniform convergence is assumed:
- If
is a sequence of Riemann integrable functions which uniformly converge with limit 
, then 
is Riemann integrable and its integral can be computed as the limit of the integrals of the 
.
Much stronger theorems in this respect, which require not much more than pointwise convergence, can be obtained if one abandons the Riemann integral and uses the Lebesgue integral
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
instead.
- If
is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
interval (or in general a compact topological space), and
is a monotone increasing sequence (meaning 
for all n and x) of continuous functions with a pointwise limit 
which is also continuous, then the convergence is necessarily uniform (Dini's theorem). Uniform convergence is also guaranteed if 
is a compact interval and 
is an equicontinuousEquicontinuityIn mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein...
sequence that converges pointwise.
Almost uniform convergence
If the domain of the functions is a measure space then the related notion of almost uniform convergence can be defined. We say a sequence of functions converges almost uniformly on E if there is a measurable subset F of E with arbitrarily small measure such that the sequence converges uniformly on the complement E \ F.Note that almost uniform convergence of a sequence does not mean that the sequence converges uniformly almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
as might be inferred from the name.
Egorov's theorem
Egorov's theorem
In measure theory, an area of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions...
guarantees that on a finite measure space, a sequence of functions that converges almost everywhere also converges almost uniformly on the same set.
Almost uniform convergence implies almost everywhere convergence and convergence in measure
Convergence in measure
Convergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
.
External links
- Graphic examples of uniform convergence of Fourier series from the University of Colorado