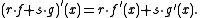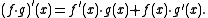Formal derivative
Encyclopedia
In mathematics
, the formal derivative is an operation on elements of a polynomial ring
or a ring of formal power series
that mimics the form of the derivative from calculus
. Though they appear similar, the algebraic advantage of a formal derivative is that it does not rely on the notion of a limit
, which is in general impossible to define for a ring
. Many of the properties of the derivative are true of the formal derivative, but some, especially those that make numerical statements, are not. The primary use of formal differentiation in algebra is to test for multiple roots of a polynomial.
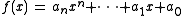
then its formal derivative is
just as for polynomials over the real or complex numbers.
These two properties make D a derivation
on A (see also module of relative differential forms for a discussion of a generalization).
, and in this situation we can define multiplicity of roots; namely, for every polynomial f(x) and every element r of R, there exists a nonnegative integer mr and a polynomial g(x) such that
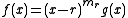
where g(r) is not equal to 0. mr is the multiplicity of r as a root of f. It follows from the Leibniz rule that in this situation, mr is also the number of differentiations that must be performed on f(x) before r is not a root of the resulting polynomial. The utility of this observation is that although in general not every polynomial of degree n in R[x] has n roots counting multiplicity (this is the maximum, by the above theorem), we may pass to field extension
s in which this is true (namely, algebraic closure
s). Once we do, we may uncover a multiple root that was not a root at all simply over R. For example, if R is the field with three elements, the polynomial
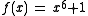
has no roots in R; however, its formal derivative is zero since 3 = 0 in R and in any extension of R, so when we pass to the algebraic closure it has a multiple root that could not have been detected by factorization in R itself. Thus, formal differentiation allows an effective
notion of multiplicity. This is important in Galois theory
, where the distinction is made between separable field extensions (defined by polynomials with no multiple roots) and inseparable ones.
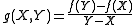
then it is not hard to verify that g(X,X) (in R[X]) coincides with the formal derivative of f as it was defined above.
This formulation of the derivative works equally well for a formal power series, assuming only that the ring of scalars is commutative.
Actually, if the division in this definition is carried out in the class of functions of
continuous at 
, it will recapture the classical definition of the derivative. If it is carried out in the class of functions continuous in both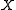 
and 
, we get uniform differentiability, and our function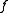 
will be continuously differentiable. Likewise, by choosing different classes of functions (say, the Lipschitz class), we get different flavors of differentiability. This way differentiation becomes a part of algebra of functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the formal derivative is an operation on elements of a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
or a ring of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
that mimics the form of the derivative from calculus
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. Though they appear similar, the algebraic advantage of a formal derivative is that it does not rely on the notion of a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, which is in general impossible to define for a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. Many of the properties of the derivative are true of the formal derivative, but some, especially those that make numerical statements, are not. The primary use of formal differentiation in algebra is to test for multiple roots of a polynomial.
Definition
The definition of a formal derivative is as follows: fix a ring R (not necessarily commutative) and let A = R[x] be the ring of polynomials over R. Then the formal derivative is an operation on elements of A, where if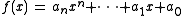then its formal derivative is
just as for polynomials over the real or complex numbers.
Properties
It can be verified that:- Formal differentiation is linear: for any two polynomials f(x), g(x) and elements r, s of R, we have
- When R is not commutative there is another, different linearity property in which r and s appear on the right rather than on the left. When R does not contain an identity element then neither of these reduces to the case of simply a sum of polynomials or the sum of a polynomial with a multiple of another polynomial, which must also be included as a "linearity" property.
- The formal derivative satisfies the Leibniz ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, or product rule:
- Note the order of the factors; when R is not commutative this is important.
These two properties make D a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on A (see also module of relative differential forms for a discussion of a generalization).
Application to finding repeated factors
As in calculus, the derivative detects multiple roots: if R is a field then R[x] is a Euclidean domainEuclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
, and in this situation we can define multiplicity of roots; namely, for every polynomial f(x) and every element r of R, there exists a nonnegative integer mr and a polynomial g(x) such that
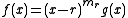
where g(r) is not equal to 0. mr is the multiplicity of r as a root of f. It follows from the Leibniz rule that in this situation, mr is also the number of differentiations that must be performed on f(x) before r is not a root of the resulting polynomial. The utility of this observation is that although in general not every polynomial of degree n in R[x] has n roots counting multiplicity (this is the maximum, by the above theorem), we may pass to field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s in which this is true (namely, algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
s). Once we do, we may uncover a multiple root that was not a root at all simply over R. For example, if R is the field with three elements, the polynomial
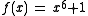
has no roots in R; however, its formal derivative is zero since 3 = 0 in R and in any extension of R, so when we pass to the algebraic closure it has a multiple root that could not have been detected by factorization in R itself. Thus, formal differentiation allows an effective
Computability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
notion of multiplicity. This is important in Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, where the distinction is made between separable field extensions (defined by polynomials with no multiple roots) and inseparable ones.
Correspondence to analytic derivative
When the ring R of scalars is commutative, there is an alternative and equivalent definition of the formal derivative, which resembles the one seen in differential calculus. The element Y-X of the ring R[X,Y] divides Yn - Xn for any nonnegative integer n, and therefore divides f(Y) - f(X) for any polynomial f in one indeterminate. If we denote the quotient (in R[X,Y]) by g: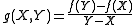then it is not hard to verify that g(X,X) (in R[X]) coincides with the formal derivative of f as it was defined above.
This formulation of the derivative works equally well for a formal power series, assuming only that the ring of scalars is commutative.
Actually, if the division in this definition is carried out in the class of functions of
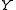continuous at 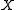, it will recapture the classical definition of the derivative. If it is carried out in the class of functions continuous in both 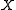and , we get uniform differentiability, and our function 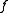will be continuously differentiable. Likewise, by choosing different classes of functions (say, the Lipschitz class), we get different flavors of differentiability. This way differentiation becomes a part of algebra of functions.See also
- DerivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
- Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
- Module of relative differential forms
- Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
- Formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
- Pincherle derivative