
Decimal
Encyclopedia
- This article aims to be an accessible introduction. For the mathematical definition, see Decimal representation.
The decimal numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
(also called base ten or occasionally denary) has ten
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
as its base. It is the numerical base most widely used by modern civilizations.
Decimal notation often refers to a base-10 positional notation
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
such as the Hindu-Arabic numeral system
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
; however, it can also be used more generally to refer to non-positional systems such as Roman
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
or Chinese numerals
Chinese numerals
Chinese numerals are characters for writing numbers in Chinese. Today speakers of Chinese use three numeral systems:the ubiquitous Arabic numerals and two indigenous systems....
which are also based on powers of ten.
Decimals also refer to decimal fractions, either separately or in contrast to vulgar fractions. In this context, a decimal is a tenth part, and decimals become a series of nested tenths. There was a notation in use like 'tenth-metre', meaning the tenth decimal of the metre, currently an Angstrom. The contrast here is between decimals and vulgar fractions, and decimal divisions and other divisions of measures, like the inch. It is possible to follow a decimal expansion with a vulgar fraction; this is done with the recent divisions of the troy ounce, which has three places of decimals, followed by a trinary place.
Decimal notation
Decimal notation is the writing of numberNumber
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s in a base-10 numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
. Examples are Roman numerals
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
, Brahmi numerals, and Chinese numerals
Chinese numerals
Chinese numerals are characters for writing numbers in Chinese. Today speakers of Chinese use three numeral systems:the ubiquitous Arabic numerals and two indigenous systems....
, as well as the Hindu-Arabic numerals used by speakers of many European languages. Roman numerals have symbols for the decimal powers (1, 10, 100, 1000) and secondary symbols for half these values (5, 50, 500). Brahmi numerals have symbols for the nine numbers 1–9, the nine decades 10–90, plus a symbol for 100 and another for 1000. Chinese numerals have symbols for 1–9, and additional symbols for powers of 10, which in modern usage reach 1044.
However, when people who use Hindu-Arabic numerals speak of decimal notation, they often mean not just decimal numeration, as above, but also decimal fractions, all conveyed as part of a positional
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
system. Positional decimal systems include a zero and use symbols (called digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
) for the ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent any number, no matter how large or how small. These digits are often used with a decimal separator
Decimal separator
Different symbols have been and are used for the decimal mark. The choice of symbol for the decimal mark affects the choice of symbol for the thousands separator used in digit grouping. Consequently the latter is treated in this article as well....
which indicates the start of a fractional part, and with a symbol such as the plus sign + (for positive) or minus sign − (for negative) adjacent to the numeral to indicate whether it is greater or less than zero, respectively.
Positional notation uses positions for each power of ten: units, tens, hundreds, thousands, etc. The position of each digit within a number denotes the multiplier (power of ten) multiplied with that digit—each position has a value ten times that of the position to its right. There were at least two presumably independent sources of positional decimal systems in ancient civilization: the Chinese counting rod
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
system and the Hindu-Arabic numeral system
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
(the latter descended from Brahmi numerals).
Ten
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
is the number which is the count of fingers and thumbs on both hands (or toes on the feet). The English word digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
as well as its translation in many languages is also the anatomical term for fingers and toes. In English, decimal (decimus < Lat.
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
) means tenth, decimate means reduce by a tenth, and denary (denarius < Lat.) means the unit of ten.
The symbols for the digits in common use around the globe
Globe
A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...
today are called Arabic numerals by Europeans and Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Arabs, the two groups' terms both referring to the culture from which they learned the system. However, the symbols used in different areas are not identical; for instance, Western Arabic numerals (from which the European numerals
European numerals
-Old-style numerals:The numerals used by Western countries have two forms: lining figures as seen on a typewriter and taught in North America, and old-style figures, in which numerals 0, 1, and 2 are at x-height; numerals 6 and 8 have bowls within x-height, and ascenders; numerals 3, 5, 7, and 9...
are derived) differ from the forms used by other Arab cultures.
Decimal fractions
A decimal fraction is a fractionFraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
whose denominator is a power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of ten.
Decimal fractions are commonly expressed without a denominator, the decimal separator being inserted into the numerator (with leading zero
Leading zero
A leading zero is any 0 digits, that lead a number string in a positional notation. For example, James Bond's famous identifier, 007, has two leading zeros. Leading zeros occupy most significant digits, which could be left blank or omitted for the same numeric value...
s added if needed) at the position from the right corresponding to the power of ten of the denominator; e.g., 8/10, 83/100, 83/1000, and 8/10000 are expressed as 0.8, 0.83, 0.083, and 0.0008. In English-speaking and many Asian countries, a period (.) or raised period (·) is used as the decimal separator; in many other countries, a comma is used.
The integer part or integral part of a decimal number is the part to the left of the decimal separator (see also truncation
Truncation
In mathematics and computer science, truncation is the term for limiting the number of digits right of the decimal point, by discarding the least significant ones.For example, consider the real numbersThe result would be:- Truncation and floor function :...
). The part from the decimal separator to the right is the fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
; if considered as a separate number, a zero is often written in front. Especially for negative numbers, we have to distinguish between the fractional part of the notation and the fractional part of the number itself, because the latter gets its own decimal sign. It is usual for a decimal number whose absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
is less than one to have a leading zero.
Trailing zero
Trailing zero
In mathematics, trailing zeros are a sequence of 0s in the decimal representation of a number, after which no other digits follow....
s after the decimal point are not necessary, although in science, engineering and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
they can be retained to indicate a required precision or to show a level of confidence in the accuracy of the number: Although 0.080 and 0.08 are numerically equal, in engineering 0.080 suggests a measurement with an error of up to one part in two thousand (±0.0005), while 0.08 suggests a measurement with an error of up to one in two hundred (see significant figures
Significant figures
The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
).
Other rational numbers
Any rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
with a denominator whose only prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s are 2 and/or 5 may be precisely expressed as a decimal fraction and has a finite decimal expansion.
- 1/2 = 0.5
- 1/20 = 0.05
- 1/5 = 0.2
- 1/50 = 0.02
- 1/4 = 0.25
- 1/40 = 0.025
- 1/25 = 0.04
- 1/8 = 0.125
- 1/125= 0.008
- 1/10 = 0.1
If the rational number's denominator has any prime factors other than 2 or 5, it cannot be expressed as a finite decimal fraction, and has a unique infinite decimal expansion ending with recurring decimals.
- 1/3 = 0.333333… (with 3 repeating)
- 1/9 = 0.111111… (with 1 repeating)
100-1=99=9×11
- 1/11 = 0.090909… (with 09 repeating)
1000-1=9×111=27×37
- 1/27 = 0.037037037…
- 1/37 = 0.027027027…
- 1/111 = 0 .009009009…
also:
- 1/81= 0.012345679012… (with 012345679 repeating)
Other prime factors in the denominator will give longer recurring sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s; see for instance 1/7, and 1/13.
That a rational number must have a finite or recurring decimal expansion can be seen to be a consequence of the long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, in that there are only q-1 possible nonzero remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
s on division by q, so that the recurring pattern will have a period less than q. For instance, to find 3/7 by long division:
0.4 2 8 5 7 1 4 ...
7 ) 3.0 0 0 0 0 0 0 0
2 8 30/7 = 4 r 2
2 0
1 4 20/7 = 2 r 6
6 0
5 6 60/7 = 8 r 4
4 0
3 5 40/7 = 5 r 5
5 0
4 9 50/7 = 7 r 1
1 0
7 10/7 = 1 r 3
3 0
2 8 30/7 = 4 r 2
2 0
etc.
The converse to this observation is that every recurring decimal represents a rational number p/q. This is a consequence of the fact that the recurring part of a decimal representation is, in fact, an infinite geometric series which will sum to a rational number. For instance,

Real numbers
Every real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
has a (possibly infinite) decimal representation; i.e., it can be written as

where
- sign is the sign functionSign functionIn mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
, and - ai ∈ { 0,1,…,9 } for all i ∈ Z are its decimal digits, equal to zero for all i greater than some number (that number being the common logarithmCommon logarithmThe common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L...
of |x|).
Such a sum converges as i increases, even if there are infinitely many non-zero ai.
Rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (e.g., p/q) with prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s in the denominator other than 2 and 5 (when reduced to simplest terms) have a unique recurring decimal representation.
Non-uniqueness of decimal representation
Consider those rational numbers which have only the factors 2 and 5 in the denominator, i.e., which can be written as p/(2a5b). In this case there is a terminating decimal representation. For instance, 1/1 = 1, 1/2 = 0.5, 3/5 = 0.6, 3/25 = 0.12 and 1306/1250 = 1.0448. Such numbers are the only real numbers which do not have a unique decimal representation, as they can also be written as a representation that has a recurring 9, for instance 1 = 0.99999…0.999...
In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
, 1/2 = 0.499999…, etc. The number 0
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
= 0/1 is special in that it has no representation with recurring 9.
This leaves the irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s. They also have unique infinite decimal representations, and can be characterised as the numbers whose decimal representations neither terminate nor recur.
So in general the decimal representation is unique, if one excludes representations that end in a recurring 9.
The same trichotomy holds for other base-n positional numeral systems
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
:
- Terminating representation: rational where the denominator divides some nk
- Recurring representation: other rational
- Non-terminating, non-recurring representation: irrational
A version of this even holds for irrational-base numeration systems, such as golden mean base representation.
Decimal computation
Decimal computation was carried out in ancient times in many ways, typically on sand tables or with a variety of abaciAbacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
.
Modern computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
hardware and software systems commonly use a binary representation
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
internally (although many early computers, such as the ENIAC
ENIAC
ENIAC was the first general-purpose electronic computer. It was a Turing-complete digital computer capable of being reprogrammed to solve a full range of computing problems....
or the IBM 650
IBM 650
The IBM 650 was one of IBM’s early computers, and the world’s first mass-produced computer. It was announced in 1953, and over 2000 systems were produced between the first shipment in 1954 and its final manufacture in 1962...
, used decimal representation internally).
For external use by computer specialists, this binary representation is sometimes presented in the related octal
Octal
The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three...
or hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
systems.
For most purposes, however, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; computer programs express literals in decimal by default. (123.1, for example, is written as such in a computer program, even though many computer languages are unable to encode that number precisely.)
Both computer hardware and software also use internal representations which are effectively decimal for storing decimal values and doing arithmetic. Often this arithmetic is done on data which are encoded using some variant of binary-coded decimal
Binary-coded decimal
In computing and electronic systems, binary-coded decimal is a digital encoding method for numbers using decimal notation, with each decimal digit represented by its own binary sequence. In BCD, a numeral is usually represented by four bits which, in general, represent the decimal range 0 through 9...
,
especially in database implementations, but there are other decimal representations in use (such as in the new IEEE 754 Standard for Floating-Point Arithmetic).
Decimal arithmetic is used in computers so that decimal fractional results can be computed exactly, which is not possible using a binary fractional representation.
This is often important for financial and other calculations.
History
Many ancient cultures calculated from early on with numerals based on ten: Egyptian hieroglyphsEgyptian hieroglyphs
Egyptian hieroglyphs were a formal writing system used by the ancient Egyptians that combined logographic and alphabetic elements. Egyptians used cursive hieroglyphs for religious literature on papyrus and wood...
, in evidence since around 3000 BC, used a purely decimal system, just as the Cretan hieroglyphs
Cretan hieroglyphs
Cretan hieroglyphs are hieroglyphs found on artifacts of Bronze Age Minoan Crete . Symbol inventories have been compiled by Evans , Meijer , Olivier/Godart...
(ca. 1625−1500 BC) of the Minoans whose numerals are closely based on the Egyptian model. The decimal system was handed down to the consecutive Bronze Age cultures of Greece, including Linear A
Linear A
Linear A is one of two scripts used in ancient Crete before Mycenaean Greek Linear B; Cretan hieroglyphs is the second script. In Minoan times, before the Mycenaean Greek dominion, Linear A was the official script for the palaces and religious activities, and hieroglyphs were mainly used on seals....
(ca. 18th century BC−1450 BC) and Linear B
Linear B
Linear B is a syllabic script that was used for writing Mycenaean Greek, an early form of Greek. It pre-dated the Greek alphabet by several centuries and seems to have died out with the fall of Mycenaean civilization...
(ca. 1375−1200 BC) — the number system of classical Greece
Classical Greece
Classical Greece was a 200 year period in Greek culture lasting from the 5th through 4th centuries BC. This classical period had a powerful influence on the Roman Empire and greatly influenced the foundation of Western civilizations. Much of modern Western politics, artistic thought, such as...
also used powers of ten, including, like the Roman numerals
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
did, an intermediate base of 5. Notably, the polymath Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
(c. 287–212 BC) invented a decimal positional system in his Sand Reckoner
The Sand Reckoner
The Sand Reckoner is a work by Archimedes in which he set out to determine an upper bound for the number of grains of sand that fit into the universe. In order to do this, he had to estimate the size of the universe according to the then-current model, and invent a way to talk about extremely...
which was based on 108 and later led the German mathematician Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
to lament what heights science would have already reached in his days if Archimedes had fully realized the potential of his ingenious discovery. The Hittites
Hittites
The Hittites were a Bronze Age people of Anatolia.They established a kingdom centered at Hattusa in north-central Anatolia c. the 18th century BC. The Hittite empire reached its height c...
hieroglyphs (since 15th century BC), just like the Egyptian and early numerals in Greece, was strictly decimal.
The Egyptian herratic numerals, the Greek alphabet numerals, the Roman numerals, the Chinese numerals and early Indian Brahmi numerals are all non-positional decimal systems, and required large numbers of symbols. For instance, Egyptian numerals used different symbols for 10, 20, through 90, 100, 200, through 900, 1000, 2000, 3000, 4000, to 10,000.
History of decimal fractions
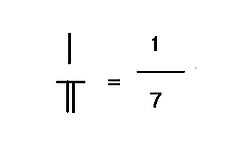
Joseph Needham
Noel Joseph Terence Montgomery Needham, CH, FRS, FBA , also known as Li Yuese , was a British scientist, historian and sinologist known for his scientific research and writing on the history of Chinese science. He was elected a fellow of the Royal Society in 1941, and as a fellow of the British...
, decimal fractions were first developed and used by the Chinese in the 1st century BC, and then spread to the Middle East and from there to Europe. The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional.
Qin Jiushao in his book Mathematical Treatise in Nine Sections
Mathematical Treatise in Nine Sections
The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
(1247) denoted 0.96644 by
-
-
-
-
- 寸





 , meaning
, meaning
-
-
-
-
-
-
-
- 寸
- 096644
-
-
-
Immanuel Bonfils invented decimal fractions around 1350, anticipating Simon Stevin
Simon Stevin
Simon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...
, but did not develop any notation to represent them.
The Persian mathematician Jamshīd al-Kāshī
Jamshid al-Kashi
Ghiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
claimed to have discovered decimal fractions himself in the 15th century, though J. Lennart Berggren notes that positional decimal fractions were used five centuries before him by Arab mathematician Abu'l-Hasan al-Uqlidisi
Abu'l-Hasan al-Uqlidisi
Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
as early as the 10th century.
Khwarizmi
Muhammad ibn Musa al-Khwarizmi
'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
introduced fractions to Islamic countries in the early 9th century. His representation of fractions was taken from traditional Chinese mathematical fractions. This form of fraction with the numerator on top and the denominator on the bottom, without a horizontal bar, was also used in the 10th century by Abu'l-Hasan al-Uqlidisi
Abu'l-Hasan al-Uqlidisi
Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
and again in the 15th century work "Arithmetic Key" by Jamshīd al-Kāshī
Jamshid al-Kashi
Ghiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
.
A forerunner of modern European decimal notation was introduced by Simon Stevin
Simon Stevin
Simon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...
in the 16th century.
Natural languages
A straightforward decimal rank system with a word for each order 10十,100百,1000千,10000万, and in which 11 is expressed as ten-one and 23 as two-ten-three, and 89345 is expressed as 8万9千3百4十5 is found in Chinese languageChinese language
The Chinese language is a language or language family consisting of varieties which are mutually intelligible to varying degrees. Originally the indigenous languages spoken by the Han Chinese in China, it forms one of the branches of Sino-Tibetan family of languages...
s, and in Vietnamese
Vietnamese language
Vietnamese is the national and official language of Vietnam. It is the mother tongue of 86% of Vietnam's population, and of about three million overseas Vietnamese. It is also spoken as a second language by many ethnic minorities of Vietnam...
with a few irregularities. Japanese
Japanese language
is a language spoken by over 130 million people in Japan and in Japanese emigrant communities. It is a member of the Japonic language family, which has a number of proposed relationships with other languages, none of which has gained wide acceptance among historical linguists .Japanese is an...
, Korean
Korean language
Korean is the official language of the country Korea, in both South and North. It is also one of the two official languages in the Yanbian Korean Autonomous Prefecture in People's Republic of China. There are about 78 million Korean speakers worldwide. In the 15th century, a national writing...
, and Thai
Thai language
Thai , also known as Central Thai and Siamese, is the national and official language of Thailand and the native language of the Thai people, Thailand's dominant ethnic group. Thai is a member of the Tai group of the Tai–Kadai language family. Historical linguists have been unable to definitively...
have imported the Chinese decimal system. Many other languages with a decimal system have special words for the numbers between 10 and 20, and decades. For example in English 11 is "eleven" not "ten-one".
Incan languages such as Quechua
Quechua languages
Quechua is a Native South American language family and dialect cluster spoken primarily in the Andes of South America, derived from an original common ancestor language, Proto-Quechua. It is the most widely spoken language family of the indigenous peoples of the Americas, with a total of probably...
and Aymara
Aymara language
Aymara is an Aymaran language spoken by the Aymara people of the Andes. It is one of only a handful of Native American languages with over three million speakers. Aymara, along with Quechua and Spanish, is an official language of Peru and Bolivia...
have an almost straightforward decimal system, in which 11 is expressed as ten with one and 23 as two-ten with three.
Some psychologists suggest irregularities of the English names of numerals may hinder children's counting ability.
Other bases
Some cultures do, or did, use other bases of numbers.- Pre-ColumbianPre-ColumbianThe pre-Columbian era incorporates all period subdivisions in the history and prehistory of the Americas before the appearance of significant European influences on the American continents, spanning the time of the original settlement in the Upper Paleolithic period to European colonization during...
MesoamericaMesoamericaMesoamerica is a region and culture area in the Americas, extending approximately from central Mexico to Belize, Guatemala, El Salvador, Honduras, Nicaragua, and Costa Rica, within which a number of pre-Columbian societies flourished before the Spanish colonization of the Americas in the 15th and...
n cultures such as the MayaMaya numeralsMaya Numerals were a vigesimal numeral system used by the Pre-Columbian Maya civilization.The numerals are made up of three symbols; zero , one and five...
used a base-20VigesimalThe vigesimal or base 20 numeral system is based on twenty .- Places :...
system (using all twenty fingers and toeToeToes are the digits of the foot of a tetrapod. Animal species such as cats that walk on their toes are described as being digitigrade. Humans, and other animals that walk on the soles of their feet, are described as being plantigrade; unguligrade animals are those that walk on hooves at the tips of...
s). - The BabyloniaBabyloniaBabylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...
ns used a combination of decimal with base 60. - Many or all of the Chumashan languagesChumashan languagesChumashan is a family of languages that were spoken on the southern California coast by Native American Chumash people.From the Coastal plains and valleys of San Luis Obispo to Malibu), neighboring inland and Transverse Ranges valleys and canyons east to bordering the San Joaquin Valley; and on...
originally used a base-4 counting system, in which the names for numbers were structured according to multiples of 4 and 16. - Many languages use quinary number systems, including Gumatj, Nunggubuyu, Kuurn Kopan Noot and Saraveca. Of these, Gumatj is the only true 5–25 language known, in which 25 is the higher group of 5.
- Some NigeriaNigeriaNigeria , officially the Federal Republic of Nigeria, is a federal constitutional republic comprising 36 states and its Federal Capital Territory, Abuja. The country is located in West Africa and shares land borders with the Republic of Benin in the west, Chad and Cameroon in the east, and Niger in...
ns use base-12 systems - The Huli languageHuli languageHuli is a Trans–New Guinea language spoken by the Huli people of the Southern Highlands province of Papua New Guinea. It features a quindecimal numeral system.-External links:***, Brian Cheetam. Papua New Guinea Journal of Education...
of Papua New GuineaPapua New GuineaPapua New Guinea , officially the Independent State of Papua New Guinea, is a country in Oceania, occupying the eastern half of the island of New Guinea and numerous offshore islands...
is reported to have base-15 numbers. Ngui means 15, ngui ki means 15×2 = 30, and ngui ngui means 15×15 = 225. - Umbu-Ungu, also known as Kakoli, is reported to have base-24 numbers. Tokapu means 24, tokapu talu means 24×2 = 48, and tokapu tokapu means 24×24 = 576.
- Ngiti is reported to have a base-32 number system with base-4 cycles.

