
Prime factor
Encyclopedia
In number theory
, the prime factors of a positive integer
are the prime number
s that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization
, or prime factorization. A prime factor can be visualized by understanding Euclid's geometric position. He saw a whole number as a line segment, which has a smallest line segment greater than 1 that can divide equally into it.
For a prime factor p of n, the multiplicity of p is the largest exponent a for which pa divides n. The prime factorization
of a positive integer is a list of the integer's prime factors, together with their multiplicity. The fundamental theorem of arithmetic
says that every positive integer has a unique prime factorization.
To shorten prime factorization, numbers are often expressed in powers, so

For a positive integer n, the number of prime factors of n and the sum of the prime factors of n (not counting multiplicity) are examples of arithmetic function
s of n that are additive
but not completely additive.
Determining the prime factors of a number is an example of a problem frequently used to ensure cryptographic security in encryption
systems; this problem is believed to require super-polynomial time in the number of digits- it is relatively easy to construct a problem that would take longer than the known age of the Universe
to calculate on current computers using current algorithms.
Two positive integers are coprime
if and only if
they have no prime factors in common. The integer 1 is coprime to every positive integer, including itself. This is because it has no prime factors; it is the empty product
. It also follows from defining a and b as coprime if gcd(a,b)=1, so that gcd(1,b)=1 for any b>=1. Euclid's algorithm can be used to determine whether two integers are coprime without knowing their prime factors; the algorithm runs in a time that is polynomial in the number of digits involved.
The function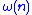 represents the number of distinct prime factors of n, while
represents the number of distinct prime factors of n, while  represents the total number of prime factors.
represents the total number of prime factors.
If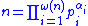 ,
,
then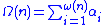 .
.
For example,
 , so:
, so: 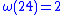 and
and 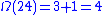 .
.
ω(n) for n = 1, 2, 3, ... is 0, 1, 1, 1, 1, 2, 1, 1, 1, ...
Ω(n) for n = 1, 2, 3, ... is 0, 1, 1, 2, 1, 2, 1, 3, 2, ...
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the prime factors of a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
are the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
, or prime factorization. A prime factor can be visualized by understanding Euclid's geometric position. He saw a whole number as a line segment, which has a smallest line segment greater than 1 that can divide equally into it.
For a prime factor p of n, the multiplicity of p is the largest exponent a for which pa divides n. The prime factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of a positive integer is a list of the integer's prime factors, together with their multiplicity. The fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
says that every positive integer has a unique prime factorization.
To shorten prime factorization, numbers are often expressed in powers, so

For a positive integer n, the number of prime factors of n and the sum of the prime factors of n (not counting multiplicity) are examples of arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
s of n that are additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
but not completely additive.
Determining the prime factors of a number is an example of a problem frequently used to ensure cryptographic security in encryption
Encryption
In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
systems; this problem is believed to require super-polynomial time in the number of digits- it is relatively easy to construct a problem that would take longer than the known age of the Universe
Age of the universe
The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...
to calculate on current computers using current algorithms.
Two positive integers are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
they have no prime factors in common. The integer 1 is coprime to every positive integer, including itself. This is because it has no prime factors; it is the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
. It also follows from defining a and b as coprime if gcd(a,b)=1, so that gcd(1,b)=1 for any b>=1. Euclid's algorithm can be used to determine whether two integers are coprime without knowing their prime factors; the algorithm runs in a time that is polynomial in the number of digits involved.
The function
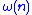 represents the number of distinct prime factors of n, while
represents the number of distinct prime factors of n, while  represents the total number of prime factors.
represents the total number of prime factors.If
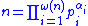 ,
,then
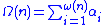 .
.For example,
 , so:
, so: 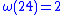 and
and 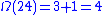 .
.ω(n) for n = 1, 2, 3, ... is 0, 1, 1, 1, 1, 2, 1, 1, 1, ...
Ω(n) for n = 1, 2, 3, ... is 0, 1, 1, 2, 1, 2, 1, 3, 2, ...
External links
- Prime Factor Calculator at the Database of Number Correlations
- A Javascript Prime Factor Calculator. Can handle numbers up to about 9×1015
- Fast Prime Factorization Calculator in JavaScript. Can handle numbers up to 1020
- Java applet: Factorization using the Elliptic Curve Method finding factors with 20+ digits
- Millions of factors and prime factors on html pages.
- List of prime factors for numbers from 2 - 5 million and growing.

