Sign function

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the sign function is an odd

Even and odd functions

In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...

 mathematical function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 that extracts the sign

Sign (mathematics)

In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...

 of a real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

. To avoid confusion with the sine

Sine

In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....

 function, this function is often called the signum function (from signum, Latin for "sign").

In mathematical expressions the sign function is often represented as sgn.

Definition

The signum function of a real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 x is defined as follows:

Properties

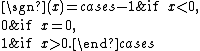
Any real number can be expressed as the product of its absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

 and its sign function:
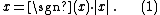
From equation (1) it follows that whenever x is not equal to 0 we have

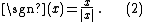
The signum function is the derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

 of the absolute value function (up to the indeterminacy at zero): Note, the resultant power of x is 0, similar to the ordinary derivative of x. The numbers cancel and all we are left with is the sign of x. .

The signum function is differentiable with derivative 0 everywhere except at 0. It is not differentiable at 0 in the ordinary sense, but under the generalised notion of differentiation in distribution theory

Distribution (mathematics)

In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...

,
the derivative of the signum function is two times the Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

,

The signum function is related to the Heaviside step function

Heaviside step function

The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....

 H_1/2(x) thus:
where the 1/2 subscript of the step function means that H_1/2(0) = 1/2. The signum can also be written using the Iverson bracket notation:
For , a smooth approximation of the sign function is
Another approximation is
which gets sharper as , note that it's the derivative of . This is inspired from the fact that the above is exactly equal for all nonzero x if , and has the advantage of simple generalization to higher dimensional analogues of the sign function (for example, the partial derivatives of ).

See Heaviside step function – Analytic approximations.

Complex signum

The signum function can be generalized to complex numbers as
for any z ∈ except z = 0. The signum of a given complex number z is the point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

 on the unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

 of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 that is nearest to z. Then, for z ≠ 0,
where arg is the complex argument function.
For reasons of symmetry, and to keep this a proper generalization of the signum function on the reals, also in the complex domain one usually defines, for z = 0:

Another generalization of the sign function for real and complex expressions is csgn, which is defined as:
where is the real part of z, is the imaginary part of z.

We then have (except for z = 0):

Generalized signum function

At real values of , it is possible to define a generalized function

Generalized function

In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...

–version of the signum function, such that
everywhere, including at the point (unlike , for which ). This generalized signum allows construction of the algebra of generalized functions, but the price of such generalization is the loss of commutativity

Commutativity

In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...

. In particular, the generalized signum anticommutes with the delta-function,
in addition, cannot be evaluated at
; and the special name, is necessary to distinguish it from the function . ( is not defined, but .)

Algebraic representation

If is a decimal number with no more than decimal digits, the signum function can be represented by means of the following algebraic expression:


where and are arbitrary integers that satisfy , and is a Kronecker delta function.

For instance, if is integer, the simplest choice is: , . On the other hand, if belongs to a set of decimal numbers with decimal digits, the simplest choice is: , .

See also

• Absolute value
  Absolute value
  In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
  
  
• Heaviside function
• Negative and non-negative numbers
  Negative and non-negative numbers
  A negative number is any real number that is less than zero. Such numbers are often used to represent the amount of a loss or absence. For example, a debt that is owed may be thought of as a negative asset, or a decrease in some quantity may be thought of as a negative increase...
  
  
• Rectangular function
• Zero crossing
  Zero crossing
  Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a "zero-crossing" is a point where the sign of a function changes Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a...