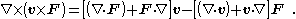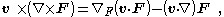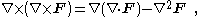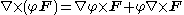
Curl
Encyclopedia
In vector calculus, the curl (or rotor) is a vector operator that describes the infinitesimal rotation
of a 3-dimensional vector field
. At every point in the field, the curl is represented by a vector. The attributes of this vector (length and direction) characterize the rotation at that point.
The direction of the curl is the axis of rotation, as determined by the right-hand rule
, and the magnitude of the curl is the magnitude of rotation. If the vector field represents the flow velocity
of a moving fluid
, then the curl is the circulation density of the fluid. A vector field whose curl is zero is called irrotational.
The curl is a form of differentiation
for vector fields. The corresponding form of the fundamental theorem of calculus
is Stokes' theorem
, which relates the surface integral
of the curl of a vector field to the line integral
of the vector field around the boundary curve.
The alternative terminology rotor or rotational and alternative notations rot F and ∇×F are often used (the former especially in many European countries, the latter, using the del
operator and the cross product
, is more used in other countries) for curl and curl F.
Unlike the gradient
and divergence
, curl does not generalize as simply to other dimensions; some generalizations are possible, but only in three dimensions is the geometrically defined curl of a vector field again a vector field. This is a similar phenomenon as in the 3 dimensional cross product
, and the connection is reflected in the notation ∇× for the curl.
The name "curl" was first suggested by James Clerk Maxwell
in 1871.
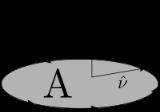
 is any unit vector, the projection of the curl of F onto
is any unit vector, the projection of the curl of F onto  is defined to be the limiting value of a closed line integral
is defined to be the limiting value of a closed line integral
in a plane orthogonal to as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.
as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.
As such, the curl operator maps C1
functions from R3 to R3 to C0 functions from R3 to R3.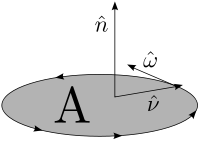 Implicitly, curl is defined by:
Implicitly, curl is defined by:

Here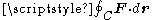 is a line integral along the boundary of the area in question, and |A| is the magnitude of the area. If
is a line integral along the boundary of the area in question, and |A| is the magnitude of the area. If 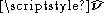 is an outward pointing in-plane normal, whereas
is an outward pointing in-plane normal, whereas 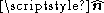 is the unit-vector perpendicular to the plane (see caption at right), then the orientation of C is chosen so that a vector
is the unit-vector perpendicular to the plane (see caption at right), then the orientation of C is chosen so that a vector 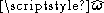 tangent to C is positively oriented
tangent to C is positively oriented
if and only if forms a positively oriented basis for R3 (right-hand rule
forms a positively oriented basis for R3 (right-hand rule
).
The above formula means that the curl of a vector field is defined as the infinitesimal area density of the circulation of that field. To this definition fit naturally (i) the Kelvin-Stokes theorem, as a global formula corresponding to the definition, and (ii) the following "easy to memorize" definition of the curl in orthogonal curvilinear coordinates, e.g. in cartesian coordinates, spherical, or cylindrical, or even elliptical or parabolical coordinates:
If (x1,x2,x3) are the Cartesian coordinates
and (u1,u2,u3) are the curvilinear coordinates, then is the length of the coordinate vector corresponding to
is the length of the coordinate vector corresponding to 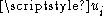 . The remaining two components of curl result from cyclic index-permutation: 3,1,2 → 1,2,3 → 2,3,1.
. The remaining two components of curl result from cyclic index-permutation: 3,1,2 → 1,2,3 → 2,3,1.
, for which simpler representations have been derived.
The notation ∇×F has its origins in the similarities to the 3 dimensional cross product
, and it is useful as a mnemonic
in Cartesian coordinates
if we take ∇ as a vector differential operator
del
. Such notation involving operators
is common in physics
and algebra
. If certain coordinate systems are used, for instance, polar-toroidal coordinates (common in plasma physics) using the notation ∇×F will yield an incorrect result.
Expanded in Cartesian coordinates
(see: Del in cylindrical and spherical coordinates
for spherical
and cylindrical coordinate
representations), ∇×F is, for F composed of [Fx, Fy, Fz]:

where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively. This expands as follows:
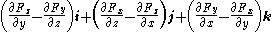
Although expressed in terms of coordinates, the result is invariant under proper rotations of the coordinate axes but the result inverts under reflection.
In a general coordinate system, the curl is given by
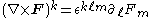
where ε denotes the Levi-Civita symbol
, the metric tensor
is used to lower the index
on F, and the Einstein summation convention implies that repeated indices are summed over. Equivalently,
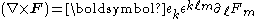
where ek are the coordinate vector fields. Equivalently, using the exterior derivative
, the curl can be expressed as:
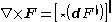
Here and
and 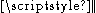 are the musical isomorphism
are the musical isomorphism
s, and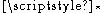 is the Hodge dual
is the Hodge dual
. This formula shows how to calculate the curl of F in any coordinate system, and how to extend the curl to any oriented
three dimensional Riemannian manifold. Since this depends on a choice of orientation, curl is a chiral
operation. In other words, if the orientation is reversed, then the direction of the curl is also reversed.
, which depends on x and y linearly:

Its plot looks like this:
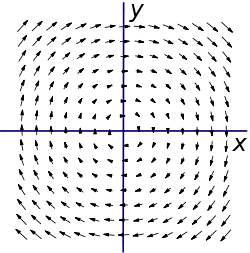 Simply by visual inspection, we can see that the field is rotating. If we place a paddle wheel
Simply by visual inspection, we can see that the field is rotating. If we place a paddle wheel
anywhere, we see immediately its tendency to rotate clockwise. Using the right-hand rule
, we expect the curl to be into the page. If we are to keep a right-handed coordinate system, into the page will be in the negative z direction. The lack of x and y directions is analogous to the cross product operation.
If we calculate the curl:
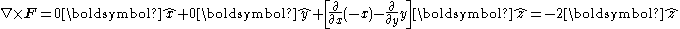
Which is indeed in the negative z direction, as expected. In this case, the curl is actually a constant, irrespective of position. The "amount" of rotation in the above vector field is the same at any point (x, y). Plotting the curl of F is not very interesting:
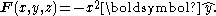
Its plot:
We might not see any rotation initially, but if we closely look at the right, we see a larger field at, say, x=4 than at x=3. Intuitively, if we placed a small paddle wheel there, the larger "current" on its right side would cause the paddlewheel to rotate clockwise, which corresponds to a curl in the negative z direction. By contrast, if we look at a point on the left and placed a small paddle wheel there, the larger "current" on its left side would cause the paddlewheel to rotate counterclockwise, which corresponds to a curl in the positive z direction. Let's check out our guess by doing the math:
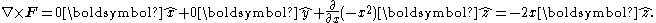
Indeed the curl is in the positive z direction for negative x and in the negative z direction for positive x, as expected. Since this curl is not the same at every point, its plot is a bit more interesting:
We note that the plot of this curl has no dependence on y or z (as it shouldn't) and is in the negative z direction for positive x and in the positive z direction for negative x.
In the case where the vector field v and ∇ are interchanged:
which introduces the Feynman subscript notation ∇F, which means the subscripted gradient operates only on the factor F.
Another example is ∇ × [ ∇ × F ]. Using Cartesian coordinates, it can be shown that:
which can be construed as a special case of the previous example with the substitution v → ∇.
(Note: represents, in the case, the vector formed by the individual laplacian of each component of the vector in question)
represents, in the case, the vector formed by the individual laplacian of each component of the vector in question)
The curl of the gradient
of any scalar field
 is always the zero vector:
is always the zero vector:
If is a scalar valued function and F is a vector field, then
is a scalar valued function and F is a vector field, then
, curl, and div
are most easily generalized and understood in the context of differential forms, which involves a number of steps. In a nutshell, they correspond to the derivatives of 0-forms, 1-forms, and 2-forms, respectively. The geometric interpretation of curl as rotation corresponds to identifying bivector
s (2-vectors) in 3 dimensions with the special orthogonal Lie algebra of infinitesimal rotations (in coordinates, skew-symmetric 3×3 matrices), while representing rotations by vectors corresponds to identifying 1-vectors (equivalently, 2-vectors) and
of infinitesimal rotations (in coordinates, skew-symmetric 3×3 matrices), while representing rotations by vectors corresponds to identifying 1-vectors (equivalently, 2-vectors) and  these all being 3-dimensional spaces.
these all being 3-dimensional spaces.
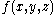 ; a differential 1-form is a linear combination of three functions
; a differential 1-form is a linear combination of three functions 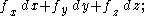 a differential 2-form is a linear combination of three functions
a differential 2-form is a linear combination of three functions  and a differential 3-form is defined by a single function:
and a differential 3-form is defined by a single function:  The exterior derivative
The exterior derivative
of a k-form is a -form, and denoting the space of k-forms by
-form, and denoting the space of k-forms by  and the exterior derivative by d yields a sequence:
and the exterior derivative by d yields a sequence: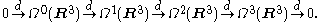
Here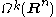 is the space of sections of the exterior algebra
is the space of sections of the exterior algebra
 vector bundle
vector bundle
over Rn, whose dimension is the binomial coefficient
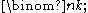 note that
note that  for
for  or
or 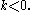 Writing only dimensions, one obtains a row of Pascal's triangle
Writing only dimensions, one obtains a row of Pascal's triangle
: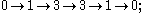
the 1-dimensional fibers correspond to functions, and the 3-dimensional fibers to vector fields, as described below. Note that modulo suitable identifications, the three nontrivial occurrences of the exterior derivative correspond to grad, curl, and div.
Differential forms and the differential can be defined on any Euclidean space, or indeed any manifold, without any notion of a Riemannian metric. On a Riemannian manifold
, or more generally pseudo-Riemannian manifold
, k-forms can be identified with k-vector fields (k-forms are k-covector fields, and a pseudo-Riemannian metric gives an isomorphism between vectors and covectors), and on an oriented vector space with a nondegenerate form (an isomorphism between vectors and covectors), there is an isomorphism between k-vectors and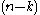 -vectors; in particular on (the tangent space of) an oriented pseudo-Riemannian manifold. Thus on an oriented pseudo-Riemannian manifold, one can interchange k-forms, k-vector fields,
-vectors; in particular on (the tangent space of) an oriented pseudo-Riemannian manifold. Thus on an oriented pseudo-Riemannian manifold, one can interchange k-forms, k-vector fields, 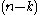 -forms, and
-forms, and 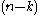 -vector fields; this is known as Hodge duality. Concretely, on
-vector fields; this is known as Hodge duality. Concretely, on 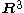 this is given by:
this is given by:
Thus, identifying 0-forms and 3-forms with functions, and 1-forms and 2-forms with vector fields:
Grad and div generalize to all oriented pseudo-Riemannian manifolds, with the same geometric interpretation, because the spaces of 0-forms and n-forms is always (fiberwise) 1-dimensional and can be identified with scalar functions, while the spaces of 1-forms and -forms are always fiberwise n-dimensional and can be identified with vector fields.
-forms are always fiberwise n-dimensional and can be identified with vector fields.
Curl does not generalize in this way to 4 or more dimensions (or down to 2 or fewer dimensions); in 4 dimensions the dimensions are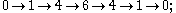
so the curl of a 1-vector field (fiberwise 4-dimensional) is a 2-vector field, which is fiberwise 6-dimensional and cannot be identified with a 1-vector field. Nor can one meaningfully go from a 1-vector field to a 2-vector field to a 3-vector field ( ), as taking the differential twice yields zero (
), as taking the differential twice yields zero ( ). Thus there is no curl function from vector fields to vector fields in other dimensions arising in this way.
). Thus there is no curl function from vector fields to vector fields in other dimensions arising in this way.
However, one can define a curl of a vector field as a 2-vector field in general, as described below.
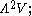 in the presence of an inner product, in coordinates these are the skew-symmetric matrices, which are geometrically considered as the special orthogonal Lie algebra
in the presence of an inner product, in coordinates these are the skew-symmetric matrices, which are geometrically considered as the special orthogonal Lie algebra 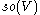 of infinitesimal rotations. This has
of infinitesimal rotations. This has 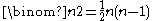 dimensions, and allows one to interpret the differential of a 1-vector field as its infinitesimal rotations. Only in 3 dimensions (or trivially in 0 dimensions) is
dimensions, and allows one to interpret the differential of a 1-vector field as its infinitesimal rotations. Only in 3 dimensions (or trivially in 0 dimensions) is 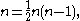 which is the most elegant and common case. is In 2 dimensions the curl of a vector field is not a vector field but a function, as 2-dimensional rotations are given by an angle (a scalar - an orientation is required to choose whether one counts clockwise or counterclockwise rotations as positive); note that this is not the div, but is rather perpendicular to it. In 3 dimensions the curl of a vector field is a vector field as is familiar (in 1 and 0 dimensions the curl of a vector field is 0, because there are no non-trivial 2-vectors), while in 4 dimensions the curl of a vector field is, geometrically, at each point an element of the 6-dimensional Lie algebra
which is the most elegant and common case. is In 2 dimensions the curl of a vector field is not a vector field but a function, as 2-dimensional rotations are given by an angle (a scalar - an orientation is required to choose whether one counts clockwise or counterclockwise rotations as positive); note that this is not the div, but is rather perpendicular to it. In 3 dimensions the curl of a vector field is a vector field as is familiar (in 1 and 0 dimensions the curl of a vector field is 0, because there are no non-trivial 2-vectors), while in 4 dimensions the curl of a vector field is, geometrically, at each point an element of the 6-dimensional Lie algebra 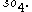
Note also that the curl of a 3-dimensional vector field which only depends on 2 coordinates (say x, y) is simply a vertical vector field (in the z direction) whose magnitude is the curl of the 2-dimensional vector field, as in the examples on this page.
Considering curl as a 2-vector field (an antisymmetric 2-tensor) has been used to generalize vector calculus and associated physics to higher dimensions.
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of a 3-dimensional vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. At every point in the field, the curl is represented by a vector. The attributes of this vector (length and direction) characterize the rotation at that point.
The direction of the curl is the axis of rotation, as determined by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
, and the magnitude of the curl is the magnitude of rotation. If the vector field represents the flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
of a moving fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
, then the curl is the circulation density of the fluid. A vector field whose curl is zero is called irrotational.
The curl is a form of differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
for vector fields. The corresponding form of the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
is Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, which relates the surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
of the curl of a vector field to the line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
of the vector field around the boundary curve.
The alternative terminology rotor or rotational and alternative notations rot F and ∇×F are often used (the former especially in many European countries, the latter, using the del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator and the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, is more used in other countries) for curl and curl F.
Unlike the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, curl does not generalize as simply to other dimensions; some generalizations are possible, but only in three dimensions is the geometrically defined curl of a vector field again a vector field. This is a similar phenomenon as in the 3 dimensional cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, and the connection is reflected in the notation ∇× for the curl.
The name "curl" was first suggested by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in 1871.
Definition
The curl of a vector field F, denoted curl F or ∇×F, at a point is defined in terms of its projection onto various lines through the point. If is any unit vector, the projection of the curl of F onto
is any unit vector, the projection of the curl of F onto  is defined to be the limiting value of a closed line integral
is defined to be the limiting value of a closed line integralLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
in a plane orthogonal to
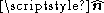 as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.
as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.As such, the curl operator maps C1
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
functions from R3 to R3 to C0 functions from R3 to R3.


Here
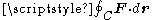 is a line integral along the boundary of the area in question, and |A| is the magnitude of the area. If
is a line integral along the boundary of the area in question, and |A| is the magnitude of the area. If 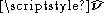 is an outward pointing in-plane normal, whereas
is an outward pointing in-plane normal, whereas 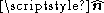 is the unit-vector perpendicular to the plane (see caption at right), then the orientation of C is chosen so that a vector
is the unit-vector perpendicular to the plane (see caption at right), then the orientation of C is chosen so that a vector 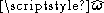 tangent to C is positively oriented
tangent to C is positively orientedOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
if and only if
 forms a positively oriented basis for R3 (right-hand rule
forms a positively oriented basis for R3 (right-hand ruleRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
).
The above formula means that the curl of a vector field is defined as the infinitesimal area density of the circulation of that field. To this definition fit naturally (i) the Kelvin-Stokes theorem, as a global formula corresponding to the definition, and (ii) the following "easy to memorize" definition of the curl in orthogonal curvilinear coordinates, e.g. in cartesian coordinates, spherical, or cylindrical, or even elliptical or parabolical coordinates:

If (x1,x2,x3) are the Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
and (u1,u2,u3) are the curvilinear coordinates, then
 is the length of the coordinate vector corresponding to
is the length of the coordinate vector corresponding to 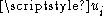 . The remaining two components of curl result from cyclic index-permutation: 3,1,2 → 1,2,3 → 2,3,1.
. The remaining two components of curl result from cyclic index-permutation: 3,1,2 → 1,2,3 → 2,3,1.Intuitive interpretation
Suppose the vector field describes the velocity field of a fluid flow (maybe a large tank of water or gas) and a small ball is located within the fluid or gas (the centre of the ball being fixed at a certain point). If the ball has a rough surface, the fluid flowing past it will make it rotate. The rotation axis (oriented according to the right hand rule) points in the direction of the curl of the field at the centre of the ball, and the angular speed of the rotation is half the value of the curl at this point.Usage
In practice, the above definition is rarely used because in virtually all cases, the curl operator can be applied using some set of curvilinear coordinatesCurvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
, for which simpler representations have been derived.
The notation ∇×F has its origins in the similarities to the 3 dimensional cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, and it is useful as a mnemonic
Mnemonic
A mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
in Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
if we take ∇ as a vector differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
. Such notation involving operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
is common in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. If certain coordinate systems are used, for instance, polar-toroidal coordinates (common in plasma physics) using the notation ∇×F will yield an incorrect result.
Expanded in Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(see: Del in cylindrical and spherical coordinates
Del in cylindrical and spherical coordinates
This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
for spherical
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
and cylindrical coordinate
Cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
representations), ∇×F is, for F composed of [Fx, Fy, Fz]:

where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively. This expands as follows:
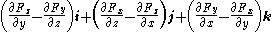
Although expressed in terms of coordinates, the result is invariant under proper rotations of the coordinate axes but the result inverts under reflection.
In a general coordinate system, the curl is given by
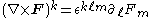
where ε denotes the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is used to lower the index
Raising and lowering indices
In mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
on F, and the Einstein summation convention implies that repeated indices are summed over. Equivalently,
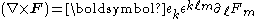
where ek are the coordinate vector fields. Equivalently, using the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, the curl can be expressed as:
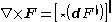
Here
 and
and 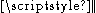 are the musical isomorphism
are the musical isomorphismMusical isomorphism
In mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
s, and
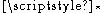 is the Hodge dual
is the Hodge dualHodge dual
In mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
. This formula shows how to calculate the curl of F in any coordinate system, and how to extend the curl to any oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
three dimensional Riemannian manifold. Since this depends on a choice of orientation, curl is a chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
operation. In other words, if the orientation is reversed, then the direction of the curl is also reversed.
A simple vector field
Take the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, which depends on x and y linearly:

Its plot looks like this:

Paddle wheel
A paddle wheel is a waterwheel in which a number of scoops are set around the periphery of the wheel. It has several usages.* Very low lift water pumping, such as flooding paddy fields at no more than about height above the water source....
anywhere, we see immediately its tendency to rotate clockwise. Using the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
, we expect the curl to be into the page. If we are to keep a right-handed coordinate system, into the page will be in the negative z direction. The lack of x and y directions is analogous to the cross product operation.
If we calculate the curl:
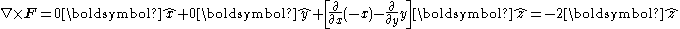
Which is indeed in the negative z direction, as expected. In this case, the curl is actually a constant, irrespective of position. The "amount" of rotation in the above vector field is the same at any point (x, y). Plotting the curl of F is not very interesting:
A more involved example
Suppose we now consider a slightly more complicated vector field: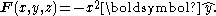
Its plot:
We might not see any rotation initially, but if we closely look at the right, we see a larger field at, say, x=4 than at x=3. Intuitively, if we placed a small paddle wheel there, the larger "current" on its right side would cause the paddlewheel to rotate clockwise, which corresponds to a curl in the negative z direction. By contrast, if we look at a point on the left and placed a small paddle wheel there, the larger "current" on its left side would cause the paddlewheel to rotate counterclockwise, which corresponds to a curl in the positive z direction. Let's check out our guess by doing the math:
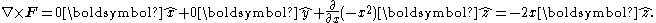
Indeed the curl is in the positive z direction for negative x and in the negative z direction for positive x, as expected. Since this curl is not the same at every point, its plot is a bit more interesting:
We note that the plot of this curl has no dependence on y or z (as it shouldn't) and is in the negative z direction for positive x and in the positive z direction for negative x.
Identities
Consider the example ∇ × [ v × F ]. Using Cartesian coordinates, it can be shown thatIn the case where the vector field v and ∇ are interchanged:
which introduces the Feynman subscript notation ∇F, which means the subscripted gradient operates only on the factor F.
Another example is ∇ × [ ∇ × F ]. Using Cartesian coordinates, it can be shown that:
which can be construed as a special case of the previous example with the substitution v → ∇.
(Note:
 represents, in the case, the vector formed by the individual laplacian of each component of the vector in question)
represents, in the case, the vector formed by the individual laplacian of each component of the vector in question)The curl of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of any scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
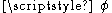 is always the zero vector:
is always the zero vector:If
 is a scalar valued function and F is a vector field, then
is a scalar valued function and F is a vector field, thenDescriptive examples
- In a vector field describing the linear velocities of each part of a rotating disk, the curl has the same value at all points.
- Of the four Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, two—Faraday's lawFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Ampère's law—can be compactly expressed using curl. Faraday's law states that the curl of an electric field is equal to the opposite of the time rate of change of the magnetic field, while Ampère's law relates the curl of the magnetic field to the current and rate of change of the electric field.
Generalizations
The vector calculus operations of gradGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, curl, and div
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
are most easily generalized and understood in the context of differential forms, which involves a number of steps. In a nutshell, they correspond to the derivatives of 0-forms, 1-forms, and 2-forms, respectively. The geometric interpretation of curl as rotation corresponds to identifying bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s (2-vectors) in 3 dimensions with the special orthogonal Lie algebra
 of infinitesimal rotations (in coordinates, skew-symmetric 3×3 matrices), while representing rotations by vectors corresponds to identifying 1-vectors (equivalently, 2-vectors) and
of infinitesimal rotations (in coordinates, skew-symmetric 3×3 matrices), while representing rotations by vectors corresponds to identifying 1-vectors (equivalently, 2-vectors) and 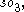 these all being 3-dimensional spaces.
these all being 3-dimensional spaces.Differential forms
In 3 dimensions, a differential 0-form is simply a function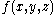 ; a differential 1-form is a linear combination of three functions
; a differential 1-form is a linear combination of three functions 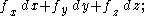 a differential 2-form is a linear combination of three functions
a differential 2-form is a linear combination of three functions  and a differential 3-form is defined by a single function:
and a differential 3-form is defined by a single function:  The exterior derivative
The exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of a k-form is a
 -form, and denoting the space of k-forms by
-form, and denoting the space of k-forms by  and the exterior derivative by d yields a sequence:
and the exterior derivative by d yields a sequence: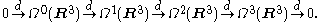
Here
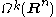 is the space of sections of the exterior algebra
is the space of sections of the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
 vector bundle
vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over Rn, whose dimension is the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
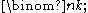 note that
note that  for
for  or
or  Writing only dimensions, one obtains a row of Pascal's triangle
Writing only dimensions, one obtains a row of Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
:
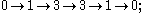
the 1-dimensional fibers correspond to functions, and the 3-dimensional fibers to vector fields, as described below. Note that modulo suitable identifications, the three nontrivial occurrences of the exterior derivative correspond to grad, curl, and div.
Differential forms and the differential can be defined on any Euclidean space, or indeed any manifold, without any notion of a Riemannian metric. On a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, or more generally pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, k-forms can be identified with k-vector fields (k-forms are k-covector fields, and a pseudo-Riemannian metric gives an isomorphism between vectors and covectors), and on an oriented vector space with a nondegenerate form (an isomorphism between vectors and covectors), there is an isomorphism between k-vectors and
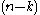 -vectors; in particular on (the tangent space of) an oriented pseudo-Riemannian manifold. Thus on an oriented pseudo-Riemannian manifold, one can interchange k-forms, k-vector fields,
-vectors; in particular on (the tangent space of) an oriented pseudo-Riemannian manifold. Thus on an oriented pseudo-Riemannian manifold, one can interchange k-forms, k-vector fields, 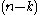 -forms, and
-forms, and 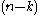 -vector fields; this is known as Hodge duality. Concretely, on
-vector fields; this is known as Hodge duality. Concretely, on 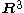 this is given by:
this is given by:
- 1-forms and 1-vector fields: the 1-form
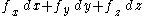 corresponds to the vector field
corresponds to the vector field 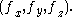
- 1-forms and 2-forms: one replaces
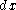 by
by 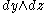 (i.e., omit dx), and likewise, taking care of orientation:
(i.e., omit dx), and likewise, taking care of orientation: 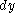 corresponds to
corresponds to 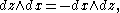 and
and  corresponds to
corresponds to 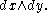 Thus
Thus 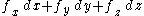 corresponds to
corresponds to 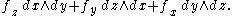
Thus, identifying 0-forms and 3-forms with functions, and 1-forms and 2-forms with vector fields:
- grad takes a function (0-form) to a vector field (1-form);
- curl takes a vector field (1-form) to a vector field (2-form);
- div takes a vector field (2-form) to a function (3-form).
Grad and div generalize to all oriented pseudo-Riemannian manifolds, with the same geometric interpretation, because the spaces of 0-forms and n-forms is always (fiberwise) 1-dimensional and can be identified with scalar functions, while the spaces of 1-forms and
 -forms are always fiberwise n-dimensional and can be identified with vector fields.
-forms are always fiberwise n-dimensional and can be identified with vector fields.Curl does not generalize in this way to 4 or more dimensions (or down to 2 or fewer dimensions); in 4 dimensions the dimensions are
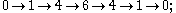
so the curl of a 1-vector field (fiberwise 4-dimensional) is a 2-vector field, which is fiberwise 6-dimensional and cannot be identified with a 1-vector field. Nor can one meaningfully go from a 1-vector field to a 2-vector field to a 3-vector field (
 ), as taking the differential twice yields zero (
), as taking the differential twice yields zero ( ). Thus there is no curl function from vector fields to vector fields in other dimensions arising in this way.
). Thus there is no curl function from vector fields to vector fields in other dimensions arising in this way.However, one can define a curl of a vector field as a 2-vector field in general, as described below.
Curl geometrically
2-vectors correspond to the exterior power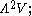 in the presence of an inner product, in coordinates these are the skew-symmetric matrices, which are geometrically considered as the special orthogonal Lie algebra
in the presence of an inner product, in coordinates these are the skew-symmetric matrices, which are geometrically considered as the special orthogonal Lie algebra 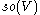 of infinitesimal rotations. This has
of infinitesimal rotations. This has 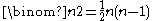 dimensions, and allows one to interpret the differential of a 1-vector field as its infinitesimal rotations. Only in 3 dimensions (or trivially in 0 dimensions) is
dimensions, and allows one to interpret the differential of a 1-vector field as its infinitesimal rotations. Only in 3 dimensions (or trivially in 0 dimensions) is 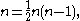 which is the most elegant and common case. is In 2 dimensions the curl of a vector field is not a vector field but a function, as 2-dimensional rotations are given by an angle (a scalar - an orientation is required to choose whether one counts clockwise or counterclockwise rotations as positive); note that this is not the div, but is rather perpendicular to it. In 3 dimensions the curl of a vector field is a vector field as is familiar (in 1 and 0 dimensions the curl of a vector field is 0, because there are no non-trivial 2-vectors), while in 4 dimensions the curl of a vector field is, geometrically, at each point an element of the 6-dimensional Lie algebra
which is the most elegant and common case. is In 2 dimensions the curl of a vector field is not a vector field but a function, as 2-dimensional rotations are given by an angle (a scalar - an orientation is required to choose whether one counts clockwise or counterclockwise rotations as positive); note that this is not the div, but is rather perpendicular to it. In 3 dimensions the curl of a vector field is a vector field as is familiar (in 1 and 0 dimensions the curl of a vector field is 0, because there are no non-trivial 2-vectors), while in 4 dimensions the curl of a vector field is, geometrically, at each point an element of the 6-dimensional Lie algebra 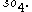
Note also that the curl of a 3-dimensional vector field which only depends on 2 coordinates (say x, y) is simply a vertical vector field (in the z direction) whose magnitude is the curl of the 2-dimensional vector field, as in the examples on this page.
Considering curl as a 2-vector field (an antisymmetric 2-tensor) has been used to generalize vector calculus and associated physics to higher dimensions.
See also
- DelDelIn vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
- GradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
- DivergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
- Nabla in cylindrical and spherical coordinates
- Vorticity
- Cross product
- Helmholtz decompositionHelmholtz decompositionIn physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...