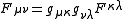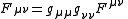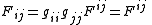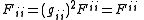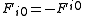Raising and lowering indices
Encyclopedia
In mathematics and mathematical physics, given a tensor
on a manifold M, in the presence of a nonsingular form on M (such as a Riemannian metric or Minkowski metric), one can raise or lower indices: change a type (k, l) tensor to a (k + 1, l − 1) tensor (raise index) or to a (k − 1, l + 1) tensor (lower index). Where the notation (k, l) has been used to denote a rank k + l with k upper indices and l lower indices.
One does this by multiplying by the covariant or contravariant metric tensor
and then contracting
(simply summing over the repeated index j in the example below).
Multiplying by the contravariant metric tensor (and contracting) raises indices:
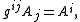
and multiplying by the covariant metric tensor (and contracting) lowers indices:

Raising and then lowering the same index (or conversely) are inverse, which is reflected in the covariant and contravariant metric tensors being inverse:
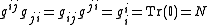
where is the identity matrix
is the identity matrix
and N is the dimension of the manifold. Note that you don't need the form to be nonsingular to lower an index, but to get the inverse (and thus raise indices) you need nonsingular.
with the metric tensor
the contravariant electromagnetic tensor
is given by
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
on a manifold M, in the presence of a nonsingular form on M (such as a Riemannian metric or Minkowski metric), one can raise or lower indices: change a type (k, l) tensor to a (k + 1, l − 1) tensor (raise index) or to a (k − 1, l + 1) tensor (lower index). Where the notation (k, l) has been used to denote a rank k + l with k upper indices and l lower indices.
One does this by multiplying by the covariant or contravariant metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and then contracting
Tensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
(simply summing over the repeated index j in the example below).
Multiplying by the contravariant metric tensor (and contracting) raises indices:
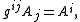
and multiplying by the covariant metric tensor (and contracting) lowers indices:

Raising and then lowering the same index (or conversely) are inverse, which is reflected in the covariant and contravariant metric tensors being inverse:
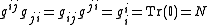
where
 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and N is the dimension of the manifold. Note that you don't need the form to be nonsingular to lower an index, but to get the inverse (and thus raise indices) you need nonsingular.
Example from Special Relativity
In a Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
with the metric tensor
the contravariant electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
is given by
-

-
- Note: some texts, such as Griffiths, will show this tensor with an overall factor of -1. This is because they used the negative of the metric tensor used here, see metric signature. Older texts such as Jackson 2ed are missing the factors of c; they are using Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
whereas here we are using SI units.
- Note: some texts, such as Griffiths, will show this tensor with an overall factor of -1. This is because they used the negative of the metric tensor used here, see metric signature. Older texts such as Jackson 2ed are missing the factors of c; they are using Gaussian units
To get the covariant tensor , we use
, we use
Note that since is diagonal, many of the terms in the formula above will vanish:
is diagonal, many of the terms in the formula above will vanish:
Using the convention of Latin letters for indices 1,2 and 3:
since both factors from the metric tensor are -1.
and similarly
Putting it all together we have:
-
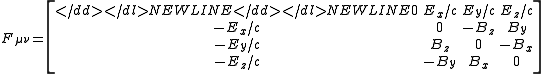
See also
- Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
- metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
- musical isomorphismMusical isomorphismIn mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
- Dual space#Bilinear products and dual spaces
- Einstein notation
-