Wigner quasi-probability distribution
Encyclopedia
The Wigner quasi-probability distribution (also called the Wigner function or the Wigner–Ville distribution after Eugene Wigner and Jean-André Ville) is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum
corrections to classical statistical mechanics
. The goal was to link the wavefunction
that appears in Schrödinger's equation to a probability distribution in phase space
.
It is a generating function
for all spatial autocorrelation
functions of a given quantum-mechanical wavefunction ψ(x).
Thus, it maps on the quantum density matrix
in the map between real phase-space functions and Hermitian
operators introduced by Hermann Weyl
in 1927, in a context related to representation theory
in mathematics (cf. Weyl quantization
in physics). In effect, it is the Weyl–Wigner transform of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal)
representation of the local time-frequency energy of a signal
.
In 1949, José Enrique Moyal
, who had derived it independently, recognized it as the quantum
moment-generating functional, and thus as the basis of an elegant encoding of all quantum expectation values, and hence quantum mechanics, in phase space (cf Weyl quantization
). It has applications in statistical mechanics
, quantum chemistry
, quantum optics
, classical optics
and signal analysis in diverse fields such as electrical engineering
, seismology
, biology
, speech processing, and engine design.
) of particles, the probability of finding a particle at a certain position in phase space is specified by a probability distribution, the Liouville density. This strict interpretation fails
for a quantum particle, due to the uncertainty principle
. Instead, the above quasi-probability Wigner distribution plays an analogous role, but does not satisfy all the properties of a conventional probability distribution; and, conversely, satisfies boundedness properties unavailable to classical distributions.
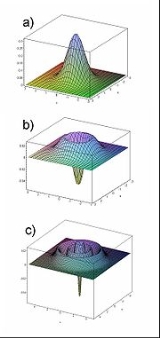
For instance, the Wigner distribution can and normally does go negative for states which have no classical model—and is a convenient indicator of quantum mechanical interference.
Smoothing the Wigner distribution through a filter of size larger than ħ (e.g., convolving with a
phase-space Gaussian to yield the Husimi representation, below), results in a positive-semidefinite function, i.e., it may be thought to have been coarsened to a semi-classical one. (Specifically, since this convolution is invertible, in fact, no information has been sacrificed, and the full quantum entropy has not increased, yet. However, if this resulting Husimi distribution is then used as a plain measure in a phase-space integral evaluation of expectation values without the requisite star product of the Husimi representation, then, at that stage, quantum
information has been forfeited and the distribution is a semi-classical one, effectively. That is, depending on its
usage in evaluating expectation values, the very same distribution may serve as a quantum or a classical distribution function.)
Regions of such negative value are provable (by convolving them with a small Gaussian) to be "small":
they cannot extend to compact regions larger than a few ħ, and hence disappear in the classical limit. They are shielded
by the uncertainty principle
, which does not allow precise location within phase-space regions smaller than ħ,
and thus renders such "negative probabilities
" less paradoxical.
where ψ is the wavefunction and x and p are position and momentum but could be any conjugate variable pair. (i.e. real and imaginary parts of the electric field or frequency and time of a signal). Note it may have support in x even in regions
where ψ has no support in x ("beats").
It is symmetric in x and p:
where φ is the Fourier transform
of ψ.
In 3D,
In the general case, which includes mixed states, it is the Wigner transform of the density matrix
:
This Wigner transformation (or map) is the inverse of the Weyl transform
, which maps phase-space functions to Hilbert-space operators, in Weyl quantization
. Thus, the Wigner function is the cornerstone of quantum mechanics
in phase space
.
In 1949, José Enrique Moyal
elucidated
how the Wigner function provides the integration measure (analogous
to a probability density function
) in phase space, to yield expectation values
from phase-space c-number
functions g(x,p) uniquely associated to suitably ordered operators
through Weyl's transform (cf. Weyl quantization
and property 7 below), in a manner evocative of classical probability theory
.
Specifically, an operator's
expectation value is a "phase-space average" of the Wigner transform of that operator,
1. P(x, p) is real
2. The x and p probability distributions are given by the marginals:
3. P(x, p) has the following reflection symmetries:
4. P(x, p) is Galilei-covariant:
5. The equation of motion for each point in the phase space is classical in the absence of forces:
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
corrections to classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The goal was to link the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
that appears in Schrödinger's equation to a probability distribution in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
It is a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for all spatial autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
functions of a given quantum-mechanical wavefunction ψ(x).
Thus, it maps on the quantum density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
in the map between real phase-space functions and Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
operators introduced by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in 1927, in a context related to representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
in mathematics (cf. Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
in physics). In effect, it is the Weyl–Wigner transform of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal)
representation of the local time-frequency energy of a signal
Wigner distribution function
The Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....
.
In 1949, José Enrique Moyal
José Enrique Moyal
José Enrique Moyal was a mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among other fields...
, who had derived it independently, recognized it as the quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
moment-generating functional, and thus as the basis of an elegant encoding of all quantum expectation values, and hence quantum mechanics, in phase space (cf Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
). It has applications in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, quantum optics
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
, classical optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
and signal analysis in diverse fields such as electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, speech processing, and engine design.
Relation to classical mechanics
A classical particle has a definite position and momentum, and hence it is represented by a point in phase space. Given a collection (ensembleStatistical ensemble (mathematical physics)
In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real...
) of particles, the probability of finding a particle at a certain position in phase space is specified by a probability distribution, the Liouville density. This strict interpretation fails
for a quantum particle, due to the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. Instead, the above quasi-probability Wigner distribution plays an analogous role, but does not satisfy all the properties of a conventional probability distribution; and, conversely, satisfies boundedness properties unavailable to classical distributions.
For instance, the Wigner distribution can and normally does go negative for states which have no classical model—and is a convenient indicator of quantum mechanical interference.
Smoothing the Wigner distribution through a filter of size larger than ħ (e.g., convolving with a
phase-space Gaussian to yield the Husimi representation, below), results in a positive-semidefinite function, i.e., it may be thought to have been coarsened to a semi-classical one. (Specifically, since this convolution is invertible, in fact, no information has been sacrificed, and the full quantum entropy has not increased, yet. However, if this resulting Husimi distribution is then used as a plain measure in a phase-space integral evaluation of expectation values without the requisite star product of the Husimi representation, then, at that stage, quantum
information has been forfeited and the distribution is a semi-classical one, effectively. That is, depending on its
usage in evaluating expectation values, the very same distribution may serve as a quantum or a classical distribution function.)
Regions of such negative value are provable (by convolving them with a small Gaussian) to be "small":
they cannot extend to compact regions larger than a few ħ, and hence disappear in the classical limit. They are shielded
by the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, which does not allow precise location within phase-space regions smaller than ħ,
and thus renders such "negative probabilities
Negative probability
In 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" where he introduced the concept of negative energies and negative probabilities:...
" less paradoxical.
Definition and meaning
The Wigner distribution P(x, p) is defined as:where ψ is the wavefunction and x and p are position and momentum but could be any conjugate variable pair. (i.e. real and imaginary parts of the electric field or frequency and time of a signal). Note it may have support in x even in regions
where ψ has no support in x ("beats").
It is symmetric in x and p:
where φ is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of ψ.
In 3D,
In the general case, which includes mixed states, it is the Wigner transform of the density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
:
This Wigner transformation (or map) is the inverse of the Weyl transform
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
, which maps phase-space functions to Hilbert-space operators, in Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
. Thus, the Wigner function is the cornerstone of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
In 1949, José Enrique Moyal
José Enrique Moyal
José Enrique Moyal was a mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among other fields...
elucidated
how the Wigner function provides the integration measure (analogous
to a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
) in phase space, to yield expectation values
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
from phase-space c-number
C-number
The term c-number is an old nomenclature used by Paul Dirac which refers to real and complex numbers. It is used to distinguish from operators in quantum mechanics....
functions g(x,p) uniquely associated to suitably ordered operators
through Weyl's transform (cf. Weyl quantizationWeyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
and property 7 below), in a manner evocative of classical probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
Specifically, an operator's
expectation value is a "phase-space average" of the Wigner transform of that operator,
Mathematical properties
2. The x and p probability distributions are given by the marginals:
If the system can be described by a pure state, one gets 
. If the system can be described by a pure state, one has 
- Typically the trace of ρ is equal to 1.
- 1. and 2. imply that P(x, p) is negative somewhere, with the exception of the coherent stateCoherent stateIn quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
(and mixtures of coherent states) and the squeezed coherent state.
3. P(x, p) has the following reflection symmetries:
- Time symmetry:
- Space symmetry:
4. P(x, p) is Galilei-covariant:
- It is not Lorentz covariant.
5. The equation of motion for each point in the phase space is classical in the absence of forces:
In fact, it is classical even in the presence of harmonic forces.
6. State overlap is calculated as:
7. Operator expectation values (averages) are calculated as
phase-space averages of the respective Wigner transforms:
8. In order that P(x, p) represent physical (positive) density matrices:
where |θ> is a pure state.
9. By virtue of the Cauchy–Schwarz inequalityCauchy–Schwarz inequalityIn mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
, for a pure state, it is constrained to be bounded,
This bound disappears in the classical limit, ħ → 0. In this limit, P(x, p) reduces to the probability density in coordinate space x, usually highly localized, multiplied by δ-functions in momentum: the classical limit
is "spiky". Thus, this quantum-mechanical bound precludes a Wigner function which is a perfectly localized delta function in phase space, as a reflection of the uncertainty principle.
The Wigner–Weyl transformation
The Wigner transformation is a general transformation of an operator
on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
to a function g(x,p) on phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
and is given by
Hermitean operators map to real functions. The inverse of this transformation,
so from phase space to Hilbert space, is called the Weyl transformationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
,
(not to be confused with another definition of the Weyl transformation). The Wigner function discussed here is the Wigner transform of the density matrixDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
operator, so the trace of an operator with the density matrix Wigner transforms to the phase-space integral overlap of g(x, p) with the Wigner function.
Evolution equation for Wigner function
The Wigner transform of the von Neumann equationDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
of the density matrix is Moyal's evolution equation for the Wigner function,
where H(x,p) is Hamiltonian and { {• , •} } is the Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
. In the classical limit ħ → 0, the Moyal bracket reduces to the Poisson bracket, while this evolution equation reduces to the Liouville equation of classical statistical mechanics.
Formally, in terms of quantum characteristicsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
, the solution of this evolution equation reads,
where
and 
are solutions of so-called quantum Hamilton's equationsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
, subject to initial conditions
and 
, and where ∗-productMoyal productIn mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
composition is understood for all argument functions. Nevertheless, in practice, evaluating such expressions is cumbersome, and concepts of classical trajectories hardly cross over to the quantum domain, as the "quantum probability fluid" diffuses, and, with few exceptions, the classical trajetory is barely discernible in an evolving Wigner distribution function.
Uses of the Wigner function outside quantum mechanics
- In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracingRay tracing (physics)In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces,...
and the full wave analysis of the system. Here p/ħ is replaced with k = |k|sinθ ≈ |k|θ in the small angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position x and angle θ while still including the effects of interference. If it becomes negative at any point then simple ray-tracing will not suffice to model the system.
- In signal analysis, a time-varying electrical signal, mechanical vibration, or sound wave are represented by a Wigner function. Here, x is replaced with the time and p/ħ is replaced with the angular frequency ω = 2πf, where f is the regular frequency.
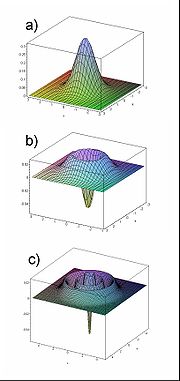
- In ultrafast optics, short laser pulses are characterized with the Wigner function using the same f and t substitutions as above. Pulse defects such as chirp (the change in frequency with time) can be visualized with the Wigner function. See Figure 2.
- In quantum optics, x and p/ħ are replaced with the X and P quadratures, the real and imaginary components of the electric field (see coherent stateCoherent stateIn quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
). The plots in Figure 1 are of quantum states of light.
Measurements of the Wigner function
- TomographyTomographyTomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
- Homodyne detectionHomodyne detectionHomodyne detection is a method of detecting frequency-modulated radiation by non-linear mixing with radiation of a reference frequency, the same principle as for heterodyne detection....
- FROGFrequency-resolved optical gatingIn optics, frequency-resolved optical gating is a derivative of autocorrelation, but is far superior in its ability to measure ultrafast optical pulse shapes...
Frequency-resolved optical gating
Other related quasi-probability distributions
The Wigner distribution was the first quasi-probability distribution to be formulated, but many more followed, formally equivalent and transformable to and from it (cf. Cohen's class distribution functionCohen's class distribution functionBilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data...
). As in the case of coordinate systems, on account of varying properties, several such have with various advantages for specific applications:- Glauber P representationGlauber P representationThe Glauber-Sudarshan P-representation is a way of writing down the state of any type of light using the coherent states as a basis. It was developed by George Sudarshan and later adopted by Roy J. Glauber...
- Husimi Q representationHusimi Q representationThe Husimi-Q distribution is a mathematical tool used in physics, and was introduced in 1940. The Q-representation is a quasi-probability distribution commonly used in quantum mechanics and also to represent the quantum state of light. It is used in the field of quantum optics and particularly...
Nevertheless, The Wigner distribution holds, in some sense, a privileged position among all these distributions, since it is
the only one whose requisite star product drops out (integrates out by parts to effective unity) in the evaluation of expectation values, as illustrated above, and so can be visualized as a quasi-probability measure analogous to the classical ones.
Historical note
As indicated, the formula for the Wigner function was independently derived several times in different contexts. In fact, apparently, Wigner was unaware that even within the context of quantum theory, it had been introduced previously by Heisenberg and DiracPaul DiracPaul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, albeit purely formally: these two missed its significance, and that of its negative values, as they merely considered it as an approximation to the full quantum description of a system such as the atom. (Incidentally, Dirac would later become Wigner's brother-in-law.) Symmetrically, in most of his legendary 18-month correspondence with MoyalJosé Enrique MoyalJosé Enrique Moyal was a mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among other fields...
in the mid 1940s, Dirac was unaware that Moyal's quantum-moment generating function was effectively the Wigner function, and it was Moyal who finally brought it to his attention.
See also
- Heisenberg group
- Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
- Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
- Modified Wigner distribution functionModified Wigner distribution functionThe Wigner distribution was first proposed for corrections to classical statistical mechanics in 1932 by Eugene Wigner. The Wigner distribution, or Wigner–Ville distribution for analytic signals, also has applications in time frequency analysis...
- Negative probabilityNegative probabilityIn 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" where he introduced the concept of negative energies and negative probabilities:...
- Cohen's class distribution functionCohen's class distribution functionBilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data...
- Wigner distribution functionWigner distribution functionThe Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....
