Cauchy–Schwarz inequality
Encyclopedia
In mathematics
, the Cauchy–Schwarz inequality (also known as the Bunyakovsky inequality, the Schwarz inequality, or the Cauchy–Bunyakovsky–Schwarz inequality), is a useful inequality encountered in many different settings, such as linear algebra
, analysis
, probability theory
, and other areas. It is considered to be one of the most important inequalities in all of mathematics. It has a number of generalizations, among them Hölder's inequality
.
The inequality for sums was published by , while the corresponding inequality for integrals was first stated by
and rediscovered by
(often misspelled "Schwartz").
,
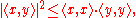
where
is the inner product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
Moreover, the two sides are equal if and only if x and y are linearly dependent
(or, in a geometrical sense, they are parallel
or one of the vectors is equal to zero).
If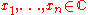
and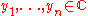 
are any complex numbers and the inner product is the standard inner product then the inequality may be restated in a more explicit way as follows:
When viewed in this way the numbers x1, ..., xn, and y1, ..., yn are the components of x and y with respect to an orthonormal
basis
of V.
Even more compactly written:
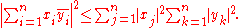
Equality holds if and only if x and y are linearly dependent, that is, one is a scalar multiple of the other (which includes the case when one or both are zero).
The finite-dimensional case of this inequality for real vectors was proved by Cauchy in 1821, and in 1859 Cauchy's student Bunyakovsky
noted that by taking limits one can obtain an integral form of Cauchy's inequality. The general result for an inner product space was obtained by Schwarz in the year 1885.
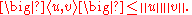
This inequality is trivial in the case v = 0, so we may assume from hereon that v is nonzero. In fact, as both sides of the inequality clearly multiply by the same factor
when 
is multiplied by a positive scaling factor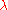 
, it suffices to consider only the case where 
is normalized to have magnitude 1, as we shall assume for convenience in the rest of this section.
Any vector can be decomposed into a sum of components parallel and perpendicular to
; in particular, 
can be decomposed into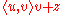 
, where 
is a vector orthogonal to 
(this orthogonality can be seen by noting that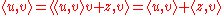 
, so that 
).
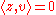Accordingly, by the Pythagorean theorem (which is to say, by simply expanding out the calculation of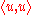
), we find that 
, with equality if and only if 
(i.e., in the case where 
is a multiple of 
). This establishes the theorem.
Rn with the standard inner product, the Cauchy–Schwarz inequality is
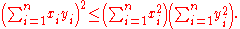
To prove this form of the inequality, consider the following quadratic polynomial in z.
Since it is nonnegative it has at most one real root in z, whence its discriminant
is less than or equal to zero, that is,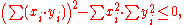
which yields the Cauchy–Schwarz inequality.
An equivalent proof for Rn starts with the summation below.
Expanding the brackets we have:
,
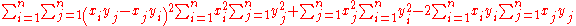collecting together identical terms (albeit with different summation indices) we find:
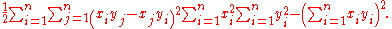
Because the left-hand side of the equation is a sum of the squares of real numbers it is greater than or equal to zero, thus:
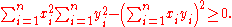
This form is used usually when solving school math problems.
Yet another approach when n ≥ 2 (n = 1 is trivial) is to consider the plane containing x and y. More precisely, recoordinatize Rn with any orthonormal basis whose first two vectors span a subspace containing x and y. In this basis only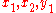
and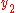 
are nonzero, and the inequality reduces to the algebra of dot product in the plane, which is related to the angle between two vectors, from which we obtain the inequality:
When n = 3 the Cauchy–Schwarz inequality can also be deduced from Lagrange's identity, which takes the form
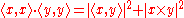
from which readily follows the Cauchy–Schwarz inequality.
, one has
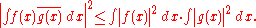
A generalization of this is the Hölder inequality.
for the inner product is often shown as a consequence of the Cauchy–Schwarz inequality, as follows: given vectors x and y:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cauchy–Schwarz inequality (also known as the Bunyakovsky inequality, the Schwarz inequality, or the Cauchy–Bunyakovsky–Schwarz inequality), is a useful inequality encountered in many different settings, such as linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and other areas. It is considered to be one of the most important inequalities in all of mathematics. It has a number of generalizations, among them Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
.
The inequality for sums was published by , while the corresponding inequality for integrals was first stated by
and rediscovered by
(often misspelled "Schwartz").
Statement of the inequality
The Cauchy–Schwarz inequality states that for all vectors x and y of an inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
,
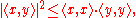
where
is the inner product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
Moreover, the two sides are equal if and only if x and y are linearly dependent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
(or, in a geometrical sense, they are parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
or one of the vectors is equal to zero).
If
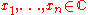and 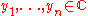are any complex numbers and the inner product is the standard inner product then the inequality may be restated in a more explicit way as follows:When viewed in this way the numbers x1, ..., xn, and y1, ..., yn are the components of x and y with respect to an orthonormal
Orthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V.
Even more compactly written:
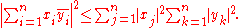
Equality holds if and only if x and y are linearly dependent, that is, one is a scalar multiple of the other (which includes the case when one or both are zero).
The finite-dimensional case of this inequality for real vectors was proved by Cauchy in 1821, and in 1859 Cauchy's student Bunyakovsky
Viktor Bunyakovsky
Viktor Yakovlevich Bunyakovsky was a Russian mathematician, member and later vice president of the Petersburg Academy of Sciences.He worked in theoretical mechanics and number theory , and is credited with an early discovery of the Cauchy-Schwarz inequality, proving it for the infinite dimensional...
noted that by taking limits one can obtain an integral form of Cauchy's inequality. The general result for an inner product space was obtained by Schwarz in the year 1885.
Proof
Let u, v be arbitrary vectors in a vector space V over F with an inner product, where F is the field of real or complex numbers. We prove the inequality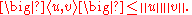This inequality is trivial in the case v = 0, so we may assume from hereon that v is nonzero. In fact, as both sides of the inequality clearly multiply by the same factor
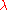when is multiplied by a positive scaling factor 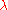, it suffices to consider only the case where is normalized to have magnitude 1, as we shall assume for convenience in the rest of this section.Any vector can be decomposed into a sum of components parallel and perpendicular to
; in particular, can be decomposed into 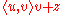, where is a vector orthogonal to (this orthogonality can be seen by noting that 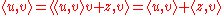, so that 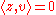).Accordingly, by the Pythagorean theorem (which is to say, by simply expanding out the calculation of
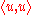), we find that , with equality if and only if (i.e., in the case where is a multiple of ). This establishes the theorem.Rn
In Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with the standard inner product, the Cauchy–Schwarz inequality is
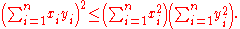
To prove this form of the inequality, consider the following quadratic polynomial in z.
Since it is nonnegative it has at most one real root in z, whence its discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
is less than or equal to zero, that is,
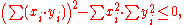
which yields the Cauchy–Schwarz inequality.
An equivalent proof for Rn starts with the summation below.
Expanding the brackets we have:
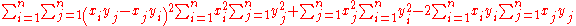,collecting together identical terms (albeit with different summation indices) we find:
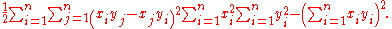
Because the left-hand side of the equation is a sum of the squares of real numbers it is greater than or equal to zero, thus:
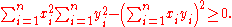
This form is used usually when solving school math problems.
Yet another approach when n ≥ 2 (n = 1 is trivial) is to consider the plane containing x and y. More precisely, recoordinatize Rn with any orthonormal basis whose first two vectors span a subspace containing x and y. In this basis only
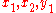and 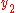are nonzero, and the inequality reduces to the algebra of dot product in the plane, which is related to the angle between two vectors, from which we obtain the inequality:When n = 3 the Cauchy–Schwarz inequality can also be deduced from Lagrange's identity, which takes the form
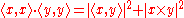
from which readily follows the Cauchy–Schwarz inequality.
L2
For the inner product space of square-integrable complex-valued functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, one has
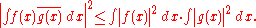
A generalization of this is the Hölder inequality.
Use
The triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
for the inner product is often shown as a consequence of the Cauchy–Schwarz inequality, as follows: given vectors x and y:
-
Taking square roots gives the triangle inequality.
The Cauchy–Schwarz inequality allows one to extend the notion of "angle between two vectors" to any real inner product space, by defining:
The Cauchy–Schwarz inequality proves that this definition is sensible, by showing that the right hand side lies in the interval [−1, 1], and justifies the notion that (real) Hilbert spaces are simply generalizations of the Euclidean space.
It can also be used to define an angle in complex inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
s, by taking the absolute value of the right hand side, as is done when extracting a metric from quantum fidelityFidelity of quantum statesIn quantum information theory, fidelity is a measure of the "closeness" of two quantum states. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space.- Motivation :...
.
The Cauchy–Schwarz is used to prove that the inner product is a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with respect to the topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
induced by the inner product itself.
The Cauchy–Schwarz inequality is usually used to show Bessel's inequalityBessel's inequalityIn mathematics, especially functional analysis, Bessel's inequality is a statement about the coefficients of an element x in a Hilbert space with respect to an orthonormal sequence....
.
Probability theory
For the multivariate case,
For the univariate case,
Indeed, for random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y, the expectation of their product is an inner product. That is,
and so, by the Cauchy–Schwarz inequality,
Moreover, if μ = E(X) and ν = E(Y), then
where Var denotes varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and Cov denotes covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
.
Generalizations
Various generalizations of the Cauchy–Schwarz inequality exist in the context of operator theoryOperator theoryIn mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, e.g. for operator-convex functions, and operator algebraOperator algebraIn functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
s, where the domain and/or range of φ are replaced by a C*-algebra or W*-algebra.
This section lists a few of such inequalities from the operator algebra setting, to give a flavor of results of this type.
Positive functionals on C*- and W*-algebras
One can discuss inner products as positive functionals. Given a Hilbert space L2(m), m being a finite measure, the inner product < · , · > gives rise to a positive functional φ by
Since < ƒ, ƒ > ≥ 0, φ(f*f) ≥ 0 for all ƒ in L2(m), where ƒ* is pointwise conjugate of ƒ. So φ is positive. Conversely every positive functional φ gives a corresponding inner product < ƒ, g >φ = φ(g*ƒ). In this language, the Cauchy–Schwarz inequality becomes
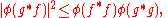
which extends verbatim to positive functionals on C*-algebras.
We now give an operator theoretic proof for the Cauchy–Schwarz inequality which passes to the C*-algebra setting. One can see from the proof that the Cauchy–Schwarz inequality is a consequence of the positivity and anti-symmetry inner-product axioms.
Consider the positive matrix
Since φ is a positive linear map whose range, the complex numbers C, is a commutative C*-algebra, φ is completely positive. Therefore
is a positive 2 × 2 scalar matrix, which implies it has positive determinant:
This is precisely the Cauchy–Schwarz inequality. If ƒ and g are elements of a C*-algebra, f* and g* denote their respective adjoints.
We can also deduce from above that every positive linear functional is bounded, corresponding to the fact that the inner product is jointly continuous.
Positive maps
Positive functionals are special cases of positive mapChoi's theorem on completely positive mapsIn mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
s. A linear map Φ between C*-algebras is said to be a positive map if a ≥ 0 implies Φ(a) ≥ 0. It is natural to ask whether inequalities of Schwarz-type exist for positive maps. In this more general setting, usually additional assumptions are needed to obtain such results.
Kadison–Schwarz inequality
The following theorem is named after Richard KadisonRichard KadisonRichard V. Kadison is an American mathematician known for his contributions to the study of operator algebras. He is a Gustave C. Kuemmerle Professor in the Department of Mathematics of the University of Pennsylvania.Kadison is a member of the U.S...
.
Theorem. If Φ is a unital positive map, then for every normal elementNormal operatorIn mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
a in its domain, we have Φ(a*a) ≥ Φ(a*)Φ(a) and Φ(a*a) ≥ Φ(a)Φ(a*).
This extends the fact φ(a*a) · 1 ≥ φ(a)*φ(a) = |φ(a)|2, when φ is a linear functional.
The case when a is self-adjoint, i.e. a = a*, is sometimes known as Kadison's inequality.
2-positive maps
When Φ is 2-positive, a stronger assumption than merely positive, one has something that looks very similar to the original Cauchy–Schwarz inequality:
Theorem (Modified Schwarz inequality for 2-positive maps) For a 2-positive map Φ between C*-algebras, for all a, b in its domain,
- i) Φ(a)*Φ(a) ≤ ||Φ(1)|| Φ(a*a).
- ii) ||Φ(a*b)||2 ≤ ||Φ(a*a)|| · ||Φ(b*b)||.
A simple argument for ii) is as follows. Consider the positive matrix
By 2-positivity of Φ,
is positive. The desired inequality then follows from the properties of positive 2 × 2 (operator) matrices.
Part i) is analogous. One can replace the matrix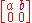
by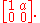 
Physics
The general formulation of the Heisenberg uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
is derived using the Cauchy–Schwarz inequality in the Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of quantum observablesObservableIn physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
.
See also
- Hölder's inequalityHölder's inequalityIn mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
- Minkowski inequalityMinkowski inequalityIn mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
- Jensen's inequalityJensen's inequalityIn mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
External links