
Statistical ensemble (mathematical physics)
Encyclopedia
In mathematical physics
, especially as introduced into statistical mechanics
and thermodynamics
by J. Willard Gibbs in 1878, an ensemble (also statistical ensemble or thermodynamic ensemble) is an idealization consisting of a large number of mental copies (sometimes infinitely many) of a system
, considered all at once, each of which represents a possible state that the real system might be in. This article treats the notion of ensembles in a mathematically rigorous fashion, although relevant physical aspects will be mentioned.
The notional size of the mental ensembles in thermodynamics, statistical mechanics and quantum statistical mechanics
can be very large indeed, to include every possible microscopic state
the system could be in, consistent with its observed macroscopic
properties. But for important physical cases it can be possible to calculate averages directly over the whole of the thermodynamic ensemble, to obtain explicit formulas for many of the thermodynamic quantities of interest, often in terms of the appropriate partition function (see below). Some of these results are presented in the statistical mechanics
article.
, one considers the phase space
of the given system. A collection of elements from the ensemble can be viewed as a swarm of representative points in the phase space. The statistical properties of the ensemble then depend on a chosen probability measure
on the phase space. If a region A of the phase space has larger measure than region B, then a system chosen at random from the ensemble is more likely to be in a microstate belonging to A than B. The choice of this measure is dictated by the specific details of the system and the assumptions one makes about the ensemble in general. For example, the phase space measure of the microcanonical ensemble
(see below) is different from that of the canonical ensemble
. The normalizing factor of the probability measure is referred to as the partition function
of the ensemble. Physically, the partition function encodes the underlying physical structure of the system.
When the measure is time-independent, the ensemble is said to be stationary.
The calculations that can be made over each of these ensembles are explored further in the article Statistical mechanics
. The main result for each ensemble however, is its characteristic state function:
Microcanonical: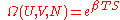
Canonical: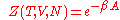
Grand canonical: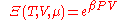
For these ensembles, the choice for the appropriate probability measure is dictated by the expressions above.
Other thermodynamic ensembles can be also defined, corresponding to different physical requirements, for which analogous formulae can often similarly be derived.
The chosen probability measure on the phase space should be a Gibbs state
of the ensemble, i.e. it should be invariant under time evolution. A standard example of this is the natural measure (locally, it is just the Lebesgue measure) on a constant energy surface for a classical mechanical system. Liouville's theorem
states this measure is invariant under the Hamiltonian flow.
Once a probability measure μ on the phase space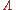 is specified, one can define the ensemble average of an observable, i.e. real-valued function f defined on
is specified, one can define the ensemble average of an observable, i.e. real-valued function f defined on 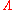 via this measure by
via this measure by
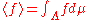 ,
,
where we have restricted to those observables which are μ-integrable.
On the other hand, let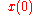 denote a representative point in the phase space, and
denote a representative point in the phase space, and 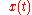 be its image under the flow, specified by the system in question, at time t. The time average of f is defined to be
be its image under the flow, specified by the system in question, at time t. The time average of f is defined to be
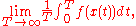
provided that this limit exists μ-almost everywhere and is independent of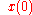 .
.
The ergodicity
requirement is that the ensemble average coincide with the time average. A sufficient condition for ergodicity is that the time evolution of the system is a mixing
. (See also ergodic hypothesis
.) Not all systems are ergodic. For instance, it is unknown at this time whether classical mechanical flows on a constant energy surface are ergodic in general. Physically, when a system fails to be ergodic, we may infer that there is more macroscopically discoverable information available about the microscopic state of the system than what we first thought. In turn this may be used to create a better-conditioned
ensemble.
Putting aside for the moment the question of how statistical ensembles are generated operationally
, we should be able to perform the following two operations on ensembles A, B of the same system:
Under certain conditions therefore, equivalence classes of statistical ensembles have the structure of a convex set. In quantum physics, a general model for this convex set is the set of density operators
on a Hilbert space
. Accordingly, there are two types of ensembles:
Thus a quantum mechanical ensemble is specified by a mixed state in general. For example, one can specify the density operators describing microcanonical, canonical, and grand canonical ensembles of quantum mechanical systems, in a mathematically rigorous fashion.
The normalization factor required for the density operator to have trace 1 is the quantum mechanical version of the partition function.
We note here that ensembles of quantum mechanical system are sometimes treated by physicists in a semi-classical fashion. Namely, one considers the phase space of the corresponding classical system (e.g. for an ensemble of quantum harmonic oscillators, the phase space of a classical harmonic oscillator is considered). Then, using physical arguments, one derives a suitable "fundamental volume" for the particular system to reflect the fact that quantum mechanical microstates are discretely distributed on the phase space. From the uncertainty principle, it is expected this fundamental volume to be related to the Planck constant,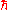 , in some way.
, in some way.
The formulation of statistical ensembles used in physics has now been widely adopted in other fields, in part because it has been recognized that the Boltzmann distribution
or Gibbs measure
serves to maximize the entropy of a system, subject to a set of constraints: this is the principle of maximum entropy
. This principle has now been widely applied to problems in linguistics
, robotics
, and the like.
In addition, statistical ensembles in physics are often built on a principle of locality
: that all interactions are only between neighboring atoms or nearby molecules. Thus, for example, lattice models
, such as the Ising model
, model ferromagnetic materials by means of nearest-neighbor interactions between spins. The statistical formulation of the principle of locality is now seen to be a form of the Markov property
in the broad sense; nearest neighbors are now Markov blanket
s. Thus, the general notion of a statistical ensemble with nearest-neighbor interactions leads to Markov random fields, which again find broad applicability; for example in Hopfield networks.
In this section we attempt to partially answer this question.
Suppose we have a preparation procedure for a system in a physics
lab: For example, the procedure might involve a physical apparatus and
some protocols for manipulating the apparatus. As a result of this preparation procedure some system
is produced and maintained in isolation for some small period of time.
By repeating this laboratory preparation procedure we obtain a
sequence of systems X1, X2,
....,Xk, which in our mathematical idealization, we assume is an infinite sequence of systems. The systems are similar in that they were all produced in the same way. This infinite sequence is an ensemble.
In a laboratory setting, each one of these prepped systems might be used as input
for one subsequent testing procedure. Again, the testing procedure
involves a physical apparatus and some protocols; as a result of the
testing procedure we obtain a yes or no answer.
Given a testing procedure E applied to each prepared system, we obtain a sequence of values
Meas (E, X1), Meas (E, X2),
...., Meas (E, Xk). Each one of these values is a 0 (or no) or a 1 (yes).
Assume the following time average exists: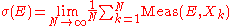
For quantum mechanical systems, an important assumption made in the
quantum logic
approach to quantum mechanics is the identification of yes-no questions to the
lattice of closed subspaces of a Hilbert space. With some additional
technical assumptions one can then infer that states are given by
density operators S so that:
We see this reflects the definition of quantum states in general: A quantum state is a mapping from the observables to their expectation values.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, especially as introduced into statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
by J. Willard Gibbs in 1878, an ensemble (also statistical ensemble or thermodynamic ensemble) is an idealization consisting of a large number of mental copies (sometimes infinitely many) of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
, considered all at once, each of which represents a possible state that the real system might be in. This article treats the notion of ensembles in a mathematically rigorous fashion, although relevant physical aspects will be mentioned.
Physical considerations
The ensemble formalises the notion that a physicist repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a range of different outcomes.The notional size of the mental ensembles in thermodynamics, statistical mechanics and quantum statistical mechanics
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
can be very large indeed, to include every possible microscopic state
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
the system could be in, consistent with its observed macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
properties. But for important physical cases it can be possible to calculate averages directly over the whole of the thermodynamic ensemble, to obtain explicit formulas for many of the thermodynamic quantities of interest, often in terms of the appropriate partition function (see below). Some of these results are presented in the statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
article.
Note on terminology
- The word "ensemble" is also used for a smaller set of possibilities sampledSample (statistics)In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
from the full set of possible states. For example, a collection of walkersRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
in a Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
iteration is called an ensemble in some literature.
- The term "ensemble" is often used in physics and physics-influenced literature. In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
literature the term probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
is more prevalent.
Ensembles of classical mechanical systems
For an ensemble of a classical mechanical systemHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, one considers the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of the given system. A collection of elements from the ensemble can be viewed as a swarm of representative points in the phase space. The statistical properties of the ensemble then depend on a chosen probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the phase space. If a region A of the phase space has larger measure than region B, then a system chosen at random from the ensemble is more likely to be in a microstate belonging to A than B. The choice of this measure is dictated by the specific details of the system and the assumptions one makes about the ensemble in general. For example, the phase space measure of the microcanonical ensemble
Microcanonical ensemble
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
(see below) is different from that of the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
. The normalizing factor of the probability measure is referred to as the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the ensemble. Physically, the partition function encodes the underlying physical structure of the system.
When the measure is time-independent, the ensemble is said to be stationary.
Principal ensembles of statistical thermodynamics
Different macroscopic environmental constraints lead to different types of ensembles, with particular statistical characteristics. The following are the most important:- Microcanonical ensembleMicrocanonical ensembleIn statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
or NVE ensemble—an ensemble of systems, each of which is required to have the same total energy (i.e. thermally isolated).
- Canonical ensembleCanonical ensembleThe canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
or NVT ensemble—an ensemble of systems, each of which can share its energy with a large heat reservoir or heat bath. The system is allowed to exchange energy with the reservoir, and the heat capacity of the reservoir is assumed to be so large as to maintain a fixed temperature for the coupled system.
- Grand canonical ensembleGrand canonical ensembleIn statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
-- an ensemble of systems, each of which is again in thermal contact with a reservoir. But now in addition to energy, there is also exchange of particles. The temperature is still assumed to be fixed.
The calculations that can be made over each of these ensembles are explored further in the article Statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The main result for each ensemble however, is its characteristic state function:
Microcanonical:
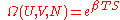
Canonical:
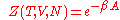
Grand canonical:
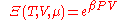
For these ensembles, the choice for the appropriate probability measure is dictated by the expressions above.
Other thermodynamic ensembles can be also defined, corresponding to different physical requirements, for which analogous formulae can often similarly be derived.
Properties of "good" ensembles
The following properties are considered desirable for a classical mechanical ensemble.- Representativeness
The chosen probability measure on the phase space should be a Gibbs state
Gibbs state
In probability theory and statistical mechanics, a Gibbs state is an equilibrium probability distribution which remains invariant under future evolution of the system...
of the ensemble, i.e. it should be invariant under time evolution. A standard example of this is the natural measure (locally, it is just the Lebesgue measure) on a constant energy surface for a classical mechanical system. Liouville's theorem
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:*In complex analysis, see Liouville's theorem ; there is also a related theorem on harmonic functions....
states this measure is invariant under the Hamiltonian flow.
- Ergodicity
Once a probability measure μ on the phase space
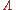 is specified, one can define the ensemble average of an observable, i.e. real-valued function f defined on
is specified, one can define the ensemble average of an observable, i.e. real-valued function f defined on 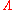 via this measure by
via this measure by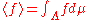 ,
,where we have restricted to those observables which are μ-integrable.
On the other hand, let
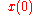 denote a representative point in the phase space, and
denote a representative point in the phase space, and 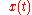 be its image under the flow, specified by the system in question, at time t. The time average of f is defined to be
be its image under the flow, specified by the system in question, at time t. The time average of f is defined to be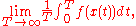
provided that this limit exists μ-almost everywhere and is independent of
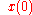 .
.The ergodicity
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
requirement is that the ensemble average coincide with the time average. A sufficient condition for ergodicity is that the time evolution of the system is a mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
. (See also ergodic hypothesis
Ergodic hypothesis
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
.) Not all systems are ergodic. For instance, it is unknown at this time whether classical mechanical flows on a constant energy surface are ergodic in general. Physically, when a system fails to be ergodic, we may infer that there is more macroscopically discoverable information available about the microscopic state of the system than what we first thought. In turn this may be used to create a better-conditioned
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
ensemble.
Ensembles in quantum statistical mechanics
Putting aside for the moment the question of how statistical ensembles are generated operationally
Operational definition
An operational definition defines something in terms of the specific process or set of validation tests used to determine its presence and quantity. That is, one defines something in terms of the operations that count as measuring it. The term was coined by Percy Williams Bridgman and is a part of...
, we should be able to perform the following two operations on ensembles A, B of the same system:
- Test whether A, B are statistically equivalent.
- If p is a real number such that 0 < p < 1, then produce a new ensemble by probabilistic sampling from A with probability p and from B with probability 1 – p.
Under certain conditions therefore, equivalence classes of statistical ensembles have the structure of a convex set. In quantum physics, a general model for this convex set is the set of density operators
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Accordingly, there are two types of ensembles:
- Pure ensembles cannot be decomposed as a convex combination of different ensembles. In quantum mechanics, a pure density matrix is one of the form
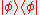 . Accordingly, a ray in a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Accordingly, a ray in a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
can be used to represent such an ensemble in quantum mechanics. A pure ensemble corresponds to having many copies of the same (up to a global phase) quantum state. - Mixed ensembles are decomposable into a convex combination of different ensembles. In general, an infinite number of distinct decompositions will be possible.
Thus a quantum mechanical ensemble is specified by a mixed state in general. For example, one can specify the density operators describing microcanonical, canonical, and grand canonical ensembles of quantum mechanical systems, in a mathematically rigorous fashion.
The normalization factor required for the density operator to have trace 1 is the quantum mechanical version of the partition function.
We note here that ensembles of quantum mechanical system are sometimes treated by physicists in a semi-classical fashion. Namely, one considers the phase space of the corresponding classical system (e.g. for an ensemble of quantum harmonic oscillators, the phase space of a classical harmonic oscillator is considered). Then, using physical arguments, one derives a suitable "fundamental volume" for the particular system to reflect the fact that quantum mechanical microstates are discretely distributed on the phase space. From the uncertainty principle, it is expected this fundamental volume to be related to the Planck constant,
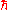 , in some way.
, in some way.Ensembles in statistics
The formulation of statistical ensembles used in physics has now been widely adopted in other fields, in part because it has been recognized that the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
or Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
serves to maximize the entropy of a system, subject to a set of constraints: this is the principle of maximum entropy
Principle of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
. This principle has now been widely applied to problems in linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, and the like.
In addition, statistical ensembles in physics are often built on a principle of locality
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
: that all interactions are only between neighboring atoms or nearby molecules. Thus, for example, lattice models
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
, such as the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, model ferromagnetic materials by means of nearest-neighbor interactions between spins. The statistical formulation of the principle of locality is now seen to be a form of the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
in the broad sense; nearest neighbors are now Markov blanket
Markov blanket
In machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes \partial A composed of A's parents, its children, and its children's other parents. In a Markov network, the Markov blanket of a node is its set of neighbouring nodes...
s. Thus, the general notion of a statistical ensemble with nearest-neighbor interactions leads to Markov random fields, which again find broad applicability; for example in Hopfield networks.
Operational interpretation
In the discussion given so far, while rigorous, we have taken for granted that the notion of an ensemble is valid a priori, as is commonly done in physical context. What has not been shown is that the ensemble itself (not the consequent results) is a precisely defined object mathematically. For instance,- It is not clear where this very large set of systems exists (for example, is it a gas of particles inside a containerGas in a boxIn quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
?)
- It is not clear how to physically generate an ensemble.
In this section we attempt to partially answer this question.
Suppose we have a preparation procedure for a system in a physics
lab: For example, the procedure might involve a physical apparatus and
some protocols for manipulating the apparatus. As a result of this preparation procedure some system
is produced and maintained in isolation for some small period of time.
By repeating this laboratory preparation procedure we obtain a
sequence of systems X1, X2,
....,Xk, which in our mathematical idealization, we assume is an infinite sequence of systems. The systems are similar in that they were all produced in the same way. This infinite sequence is an ensemble.
In a laboratory setting, each one of these prepped systems might be used as input
for one subsequent testing procedure. Again, the testing procedure
involves a physical apparatus and some protocols; as a result of the
testing procedure we obtain a yes or no answer.
Given a testing procedure E applied to each prepared system, we obtain a sequence of values
Meas (E, X1), Meas (E, X2),
...., Meas (E, Xk). Each one of these values is a 0 (or no) or a 1 (yes).
Assume the following time average exists:
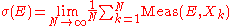
For quantum mechanical systems, an important assumption made in the
quantum logic
Quantum logic
In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
approach to quantum mechanics is the identification of yes-no questions to the
lattice of closed subspaces of a Hilbert space. With some additional
technical assumptions one can then infer that states are given by
density operators S so that:

We see this reflects the definition of quantum states in general: A quantum state is a mapping from the observables to their expectation values.
See also
- density matrixDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
- Ensemble (fluid mechanics)Ensemble (fluid mechanics)In fluid mechanics, an ensemble is an imaginary collection of notionally identical experiments.Each member of the ensemble will have nominally identical boundary conditions and fluid properties...
- Partition function (statistical mechanics)Partition function (statistical mechanics)Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
- Partition function (mathematics)Partition function (mathematics)The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
- isothermal-isobaric ensembleIsothermal-isobaric ensembleThe isothermal–isobaric ensemble is a statistical mechanical ensemble that maintains constant temperature T \, and constant pressure P \, applied. It is also called the NpT-ensemble, where the number of particles N \, is also kept as a constant...
- phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
- Liouville's theorem (Hamiltonian)Liouville's theorem (Hamiltonian)In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...

