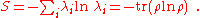Density matrix
Encyclopedia
In quantum mechanics
, a density matrix is a self-adjoint
(or Hermitian) positive-semidefinite matrix (possibly infinite dimensional) of trace
one, that describes the statistical state of a quantum system. The formalism was introduced by John von Neumann
(and, less systematically, independently by Lev Landau
and Felix Bloch
in 1927).
The density matrix is useful for describing and performing calculations with a mixed state, which is a statistical ensemble of several quantum states. (This is in contrast to a pure state, which is a quantum system that is described by a single state vector). The density matrix is the quantum-mechanical analogue to a phase-space
probability measure
(probability distribution of position and momentum) in classical statistical mechanics.
Mixed states arise in situations where there is classical uncertainty, i.e. when it is unknown by the experimenter which particular states are being manipulated. (This should not be confused with the unrelated concept of quantum uncertainty, which dictates that even if the experimenter knows which particular states are being manipulated, the results of some measurements cannot be predicted.) For example: A quantum system with an uncertain or randomly-varying preparation history (so one does not know with certainty which pure quantum state the system is in); or a quantum system in thermal equilibrium (at finite temperatures). Also, if a quantum system has two or more subsystems that are entangled
, then each individual subsystem must be treated as a mixed state even if the complete system is in a pure state; the density matrix of the subsystem is calculated as a partial trace
of the density matrix of the whole system. Relatedly, the density matrix is a crucial tool in quantum decoherence
theory. See also quantum statistical mechanics
.
The operator that is represented by the density matrix is called the density operator. (The close relationship between matrices and operators is a basic concept in linear algebra
; see the article Linear operator for details.) In practice, the terms "density matrix" and "density operator" are often used interchangeably. (When the space
of quantum states is infinite-dimensional, the term "density operator" is preferred.) The density operator, like the density matrix, is positive-semidefinite, self-adjoint
, and has trace
one.
)
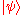. A quantum system with a state vector 
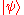is called a pure state. However, it is also possible for a system to be in a statistical ensemble of different state vectors: For example, there may be a 50% probability that the state vector is 
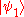and a 50% chance that the state vector is 
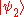. This system would be in a mixed state. The density matrix is especially useful for mixed states, because any state, pure or mixed, can be characterized by a single density matrix.
A mixed state is different from a quantum superposition
. In fact, a quantum superposition of pure states is another pure state, for example
.
, corresponding to two orthogonal quantum states,
(right circular polarization
) and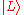
(left circular polarization
). A photon can also be in a superposition state, such as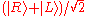
(vertical polarization) or 
(horizontal polarization). More generally, it can be in any state 
, corresponding to linear
, circular
, or elliptical polarization
.
However, unpolarized light (such as the light from an incandescent light bulb
) is different from any of these. Unlike linearly or elliptically polarized light, it passes through a polarizer
with 50% intensity loss whatever the orientation of the polarizer; and unlike circularly polarized light, it cannot be made linearly polarized with any wave plate
. Indeed, unpolarized light cannot be described as any state of the form
. However, unpolarized light can be described perfectly by assuming that each photon is either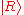 
with 50% probability or 
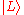with 50% probability. The same behavior would occur if each photon was either vertically polarized with 50% probability or horizontally polarized with 50% probability.
Therefore, unpolarized light cannot be described by any pure state, but can be described as a statistical ensemble of pure states in at least two ways (the ensemble of half left and half right circularly polarized, or the ensemble of half vertically and half horizontally linearly polarized). These two ensembles are completely indistinguishable experimentally, and therefore they are considered the same mixed state. One of the advantages of the density matrix is that there is just one density matrix for each mixed state, whereas there are many statistical ensembles of pure states for each mixed state. Nevertheless, the density matrix contains all the information necessary to calculate any measurable property of the mixed state.
Where do mixed states come from? To answer that, consider how to generate unpolarized light. One way is to use a system in thermal equilibrium
, a statistical mixture of enormous numbers of microstates
, each with a certain probability (the Boltzmann factor
), switching rapidly from one to the next due to thermal fluctuations
. Thermal randomness explains why an incandescent light bulb
, for example, emits unpolarized light. A second way to generate unpolarized light is to introduce uncertainty in the preparation of the system, for example, passing it through a birefringent crystal with a rough surface, so that slightly different parts of the beam acquire different polarizations. A third way to generate unpolarized light uses an EPR
setup: A radioactive decay can emit two photons traveling in opposite directions, in the quantum state
. The two photons together are in a pure state, but if you only look at one of the photons and ignore the other, the photon behaves just like unpolarized light.
More generally, mixed states commonly arise from a statistical mixture of the starting state (such as in thermal equilibrium), from uncertainty in the preparation procedure (such as slightly different paths that a photon can travel), or from looking at a subsystem entangled with something else.
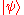of a system completely determines the statistical behavior of a measurement. As an example, take an observable quantity, and let A be the associated observable operator
which has a representation on the Hilbert space
of the quantum system. For any real-valued function F defined on the real numbers, the expectation value of F(A) is the quantity
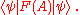
Now consider the example of a "mixed quantum system" prepared by statistically combining two different pure states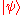
and 
, with the associated probabilities p and , respectively. The associated probabilities mean that the preparation process for the quantum system ends in the state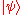 
with probability p and in the state 
with probability .
It is not hard to show that the statistical properties of the observable for the system prepared in such a mixed state are completely determined. However, there is no state vector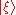
which determines this statistical behavior in the sense that the expectation value of F(A) is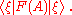
Nevertheless, there is a unique operator ρ such that the expectation value of F(A) can be written as
where the operator ρ is the density operator of the mixed system. A simple calculation shows that the operator ρ for the above example is given by
where the coefficients pj are non-negative and add up to one. This represents a statistical mixture of pure states. If the given system is closed, then one can think of a mixed state as representing a single system with an uncertain preparation history, as explicitly detailed above; or we can regard the mixed state as representing an ensemble
of systems, i.e. large number of copies of the system in question, where pj is the proportion of the ensemble being in the state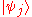
. An ensemble is described by a pure state if every copy of the system in that ensemble is in the same state, i.e. it is a pure ensemble.
If the system is not closed, however, then it is simply not correct to claim that it has some definite but unknown state vector, as the density operator may record physical entanglements to other systems.
Example Consider a quantum ensemble of size N with occupancy numbers n1, n2,...,nk corresponding to the orthonormal states
, respectively, where n1+...+nk = N, and, thus, the coefficients pj = nj /N. For a pure ensemble, where all N particles are in state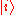 
, we have nj = 0, for all j ≠ i, from which we recover the corresponding density operator 
.
However the density operator of a mixed state does not capture all the information about a mixture; in particular, the coefficients pj and the kets ψj are not recoverable from the operator ρ without additional information. This non-uniqueness implies that different ensembles or mixtures may correspond to the same density operator. Such equivalent ensembles or mixtures cannot be distinguished by measurement of observables alone. This equivalence can be characterized precisely. Two ensembles ψ, ψ' define the same density operator if and only if
there is a matrix U with
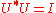
i.e., U is unitary
and such that
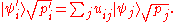
This is simply a restatement of the following fact from linear algebra: for two square matrices M and N, M M* = N N* if and only if M = NU for some unitary U. (See square root of a matrix
for more details.) Thus there is a unitary freedom in the ket mixture or ensemble that gives the same density operator. However if the kets in the mixture are orthonormal then the original probabilities pj are recoverable as the eigenvalues of the density matrix.
In operator language, a density operator is a positive semidefinite
, hermitian
operator acting on the state space of trace 1. A density operator describes a pure state if it is a rank one projection. Equivalently, a density operator ρ is a pure state if and only if
i.e. the state is idempotent. This is true regardless of whether H is finite dimensional or not.
Geometrically, when the state is not expressible as a convex combination
of other states, it is a pure state. The family of mixed states is a convex set and a state is pure if it is an extremal point of that set.
It follows from the spectral theorem for compact self-adjoint operators
that every mixed state is an infinite convex combination of pure states. This representation is not unique. Furthermore, a theorem of Andrew Gleason
states that certain functions defined on the family of projections and taking values in [0,1] (which can be regarded as quantum analogues of probability measures) are determined by unique mixed states. See quantum logic for more details.
of the system, and suppose the ensemble is in a mixed state such that each of the pure states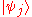
occurs with probability pj. Then the corresponding density operator is:
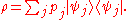
The expectation value
of the measurement can be calculated by extending from the case of pure states (see Measurement in quantum mechanics
):
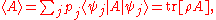
where tr denotes trace
. Moreover, if A has spectral resolution
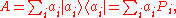
where
, the corresponding density operator after the measurement is given by:
Note that the above density operator describes the full ensemble after measurement. The sub-ensemble for which the measurement result was the particular value ai is described by the different density operator
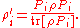
This is true assuming that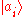
is the only eigenket (up to phase
) with eigenvalue ai; more generally, Pi in this expression would be replaced by the projection operator into the eigenspace corresponding to eigenvalue ai.
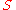of a mixture can be expressed in terms of the eigenvalues of 
or in terms of the trace
and logarithm
of the density operator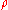
. Since 
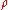is a positive semi-definite operator, it has a spectral decomposition such that 
where 
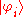are orthonormal vectors. Therefore the entropy of a quantum system with density matrix 
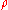is
Also it can be shown that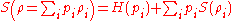
where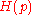
is the Shannon entropy.
This entropy can increase but never decrease with a measurement. The entropy of a pure state is zero, while that of a proper mixture always greater than zero. Therefore a pure state may be converted into a mixture by a measurement, but a proper mixture can never be converted into a pure state. Thus the act of measurement induces a fundamental irreversible
change on the density matrix; this is analogous to the "collapse" of the state vector, or wavefunction collapse
.
(A subsystem of a larger system can be turned from a mixed to a pure state, but only by increasing the von Neumann entropy elsewhere in the system. This is analogous to how the entropy of an object can be lowered by putting it in a refrigerator: The air outside the refrigerator's heat-exchanger warms up, gaining even more entropy than was lost by the object in the refrigerator. See second law of thermodynamics
.)
describes how pure states evolve in time, the von Neumann equation (also known as Liouville-von Neumann equation) describes how a density operator evolves in time (in fact, the two equations are equivalent, in the sense that either can be derived from the other.) The von Neumann equation states:
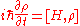
where the brackets denote a commutator
. Note that this equation is only true when the density operator is taken to be in the Schrödinger picture
even though this equation seems at first look to emulate the Heisenberg equation of motion:
where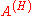
is some 'Heisenberg' operator. Taking the density operator to be in the Schrödinger picture makes sense since it is composed of 'Schrödinger' kets and bras evolved in time as per the Schrödinger picture.
If the Hamiltonian is time-independent, this differential equation can be solved to get
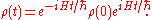
, the density matrix transforms into the Wigner function
,
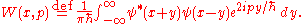
The equation for the time-evolution of the Wigner function is then the Wigner-transform of the above von Neumann equation,
where H(q,p) is the Hamiltonian, and { { •,• } } is the Moyal bracket
, the transform of the quantum commutator
.
The evolution equation for the Wigner function is then analogous to that of its classical limit, the Liouville equation of classical physics
. In the limit of vanishing Planck's constant ħ, W(q,p,t) reduces to the classical Liouville probability density function in phase space
.
The classical Liouville equation can be solved using the method of characteristics
for partial differential equations, the characteristic equations being Hamilton's equations. The Moyal equation in quantum mechanics similarly admits formal solutions in terms of quantum characteristics
, predicated on the ∗−product
of phase space, although, in actual practice, solution-seeking follows different methods.
. Then the subsystems are described by their reduced density operator.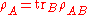
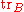is called partial trace
over system B.
If A and B are two distinct and independent systems then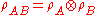
which is a product state.
are positive linear functional
s on A. However, by using the GNS construction, we can recover Hilbert spaces which realize A as a subalgebra of operators.
Geometrically, a pure state on a C*-algebra A is a state which is an extreme point of the set of all states on A. By properties of the GNS construction these states correspond to irreducible representations of A.
The states of the C*-algebra of compact operators K(H) correspond exactly to the density operators and therefore the pure states of K(H) are exactly the pure states in the sense of quantum mechanics.
The C*-algebraic formulation can be seen to include both classical and quantum systems. When the system is classical, the algebra of observables become an abelian C*-algebra. In that case the states become probability measures, as noted in the introduction.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, a density matrix is a self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
(or Hermitian) positive-semidefinite matrix (possibly infinite dimensional) of trace
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
one, that describes the statistical state of a quantum system. The formalism was introduced by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
(and, less systematically, independently by Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
and Felix Bloch
Felix Bloch
Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...
in 1927).
The density matrix is useful for describing and performing calculations with a mixed state, which is a statistical ensemble of several quantum states. (This is in contrast to a pure state, which is a quantum system that is described by a single state vector). The density matrix is the quantum-mechanical analogue to a phase-space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
(probability distribution of position and momentum) in classical statistical mechanics.
Mixed states arise in situations where there is classical uncertainty, i.e. when it is unknown by the experimenter which particular states are being manipulated. (This should not be confused with the unrelated concept of quantum uncertainty, which dictates that even if the experimenter knows which particular states are being manipulated, the results of some measurements cannot be predicted.) For example: A quantum system with an uncertain or randomly-varying preparation history (so one does not know with certainty which pure quantum state the system is in); or a quantum system in thermal equilibrium (at finite temperatures). Also, if a quantum system has two or more subsystems that are entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, then each individual subsystem must be treated as a mixed state even if the complete system is in a pure state; the density matrix of the subsystem is calculated as a partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
of the density matrix of the whole system. Relatedly, the density matrix is a crucial tool in quantum decoherence
Quantum decoherence
In quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
theory. See also quantum statistical mechanics
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
.
The operator that is represented by the density matrix is called the density operator. (The close relationship between matrices and operators is a basic concept in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
; see the article Linear operator for details.) In practice, the terms "density matrix" and "density operator" are often used interchangeably. (When the space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of quantum states is infinite-dimensional, the term "density operator" is preferred.) The density operator, like the density matrix, is positive-semidefinite, self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
, and has trace
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
one.
Pure and mixed states
In quantum mechanics, a quantum system is represented by a state vector (or ketBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
)
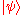. A quantum system with a state vector 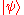is called a pure state. However, it is also possible for a system to be in a statistical ensemble of different state vectors: For example, there may be a 50% probability that the state vector is 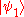and a 50% chance that the state vector is 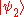. This system would be in a mixed state. The density matrix is especially useful for mixed states, because any state, pure or mixed, can be characterized by a single density matrix.A mixed state is different from a quantum superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
. In fact, a quantum superposition of pure states is another pure state, for example
.Example: Light polarization
An example of pure and mixed states is light polarization. Photons can have two helicitiesCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
, corresponding to two orthogonal quantum states,
(right circular polarizationCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
) and
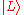(left circular polarizationCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
). A photon can also be in a superposition state, such as
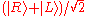(vertical polarization) or (horizontal polarization). More generally, it can be in any state , corresponding to linearLinear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
, circular
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
, or elliptical polarization
Elliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
.
However, unpolarized light (such as the light from an incandescent light bulb
Incandescent light bulb
The incandescent light bulb, incandescent lamp or incandescent light globe makes light by heating a metal filament wire to a high temperature until it glows. The hot filament is protected from air by a glass bulb that is filled with inert gas or evacuated. In a halogen lamp, a chemical process...
) is different from any of these. Unlike linearly or elliptically polarized light, it passes through a polarizer
Polarizer
A polarizer is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization. The common types of polarizers are linear polarizers and circular...
with 50% intensity loss whatever the orientation of the polarizer; and unlike circularly polarized light, it cannot be made linearly polarized with any wave plate
Wave plate
A wave plate or retarder is an optical device that alters the polarization state of a light wave travelling through it.- Operation :A wave plate works by shifting the phase between two perpendicular polarization components of the light wave. A typical wave plate is simply a birefringent crystal...
. Indeed, unpolarized light cannot be described as any state of the form
. However, unpolarized light can be described perfectly by assuming that each photon is either 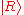with 50% probability or 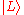with 50% probability. The same behavior would occur if each photon was either vertically polarized with 50% probability or horizontally polarized with 50% probability.Therefore, unpolarized light cannot be described by any pure state, but can be described as a statistical ensemble of pure states in at least two ways (the ensemble of half left and half right circularly polarized, or the ensemble of half vertically and half horizontally linearly polarized). These two ensembles are completely indistinguishable experimentally, and therefore they are considered the same mixed state. One of the advantages of the density matrix is that there is just one density matrix for each mixed state, whereas there are many statistical ensembles of pure states for each mixed state. Nevertheless, the density matrix contains all the information necessary to calculate any measurable property of the mixed state.
Where do mixed states come from? To answer that, consider how to generate unpolarized light. One way is to use a system in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
, a statistical mixture of enormous numbers of microstates
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
, each with a certain probability (the Boltzmann factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
), switching rapidly from one to the next due to thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
. Thermal randomness explains why an incandescent light bulb
Incandescent light bulb
The incandescent light bulb, incandescent lamp or incandescent light globe makes light by heating a metal filament wire to a high temperature until it glows. The hot filament is protected from air by a glass bulb that is filled with inert gas or evacuated. In a halogen lamp, a chemical process...
, for example, emits unpolarized light. A second way to generate unpolarized light is to introduce uncertainty in the preparation of the system, for example, passing it through a birefringent crystal with a rough surface, so that slightly different parts of the beam acquire different polarizations. A third way to generate unpolarized light uses an EPR
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
setup: A radioactive decay can emit two photons traveling in opposite directions, in the quantum state
. The two photons together are in a pure state, but if you only look at one of the photons and ignore the other, the photon behaves just like unpolarized light.More generally, mixed states commonly arise from a statistical mixture of the starting state (such as in thermal equilibrium), from uncertainty in the preparation procedure (such as slightly different paths that a photon can travel), or from looking at a subsystem entangled with something else.
Mathematical description
In quantum mechanics, the state vector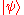 of a system completely determines the statistical behavior of a measurement. As an example, take an observable quantity, and let A be the associated observable operatorObservable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
which has a representation on the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
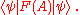
of the quantum system. For any real-valued function F defined on the real numbers, the expectation value of F(A) is the quantityNow consider the example of a "mixed quantum system" prepared by statistically combining two different pure states
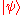and , with the associated probabilities p and , respectively. The associated probabilities mean that the preparation process for the quantum system ends in the state 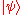with probability p and in the state with probability .It is not hard to show that the statistical properties of the observable for the system prepared in such a mixed state are completely determined. However, there is no state vector
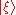which determines this statistical behavior in the sense that the expectation value of F(A) is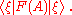Nevertheless, there is a unique operator ρ such that the expectation value of F(A) can be written as
where the operator ρ is the density operator of the mixed system. A simple calculation shows that the operator ρ for the above example is given by
Formulation
For a finite dimensional function space, the most general density operator is of the formwhere the coefficients pj are non-negative and add up to one. This represents a statistical mixture of pure states. If the given system is closed, then one can think of a mixed state as representing a single system with an uncertain preparation history, as explicitly detailed above; or we can regard the mixed state as representing an ensemble
Statistical ensemble (mathematical physics)
In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real...
of systems, i.e. large number of copies of the system in question, where pj is the proportion of the ensemble being in the state
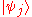. An ensemble is described by a pure state if every copy of the system in that ensemble is in the same state, i.e. it is a pure ensemble.If the system is not closed, however, then it is simply not correct to claim that it has some definite but unknown state vector, as the density operator may record physical entanglements to other systems.
Example Consider a quantum ensemble of size N with occupancy numbers n1, n2,...,nk corresponding to the orthonormal states
, respectively, where n1+...+nk = N, and, thus, the coefficients pj = nj /N. For a pure ensemble, where all N particles are in state 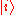, we have nj = 0, for all j ≠ i, from which we recover the corresponding density operator .However the density operator of a mixed state does not capture all the information about a mixture; in particular, the coefficients pj and the kets ψj are not recoverable from the operator ρ without additional information. This non-uniqueness implies that different ensembles or mixtures may correspond to the same density operator. Such equivalent ensembles or mixtures cannot be distinguished by measurement of observables alone. This equivalence can be characterized precisely. Two ensembles ψ, ψ' define the same density operator if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is a matrix U with
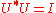
i.e., U is unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
and such that
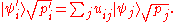
This is simply a restatement of the following fact from linear algebra: for two square matrices M and N, M M* = N N* if and only if M = NU for some unitary U. (See square root of a matrix
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
for more details.) Thus there is a unitary freedom in the ket mixture or ensemble that gives the same density operator. However if the kets in the mixture are orthonormal then the original probabilities pj are recoverable as the eigenvalues of the density matrix.
In operator language, a density operator is a positive semidefinite
Positive semidefinite
In mathematics, positive semidefinite may refer to:* positive-semidefinite matrix* positive-semidefinite function...
, hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
operator acting on the state space of trace 1. A density operator describes a pure state if it is a rank one projection. Equivalently, a density operator ρ is a pure state if and only if
-
,
i.e. the state is idempotent. This is true regardless of whether H is finite dimensional or not.
Geometrically, when the state is not expressible as a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of other states, it is a pure state. The family of mixed states is a convex set and a state is pure if it is an extremal point of that set.
It follows from the spectral theorem for compact self-adjoint operators
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
that every mixed state is an infinite convex combination of pure states. This representation is not unique. Furthermore, a theorem of Andrew Gleason
Andrew Gleason
Andrew Mattei Gleason was an American mathematician and the eponym of Gleason's theorem and the Greenwood–Gleason graph. After briefly attending Berkeley High School he graduated from Roosevelt High School in Yonkers, then Yale University in 1942, where he became a Putnam Fellow...
states that certain functions defined on the family of projections and taking values in [0,1] (which can be regarded as quantum analogues of probability measures) are determined by unique mixed states. See quantum logic for more details.
Measurement
Let A be an observableObservable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
of the system, and suppose the ensemble is in a mixed state such that each of the pure states
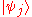occurs with probability pj. Then the corresponding density operator is: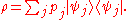The expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
of the measurement can be calculated by extending from the case of pure states (see Measurement in quantum mechanics
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
):
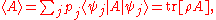
where tr denotes trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
. Moreover, if A has spectral resolution
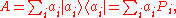
where
, the corresponding density operator after the measurement is given by:Note that the above density operator describes the full ensemble after measurement. The sub-ensemble for which the measurement result was the particular value ai is described by the different density operator
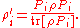
This is true assuming that
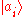is the only eigenket (up to phasePhase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
) with eigenvalue ai; more generally, Pi in this expression would be replaced by the projection operator into the eigenspace corresponding to eigenvalue ai.
Entropy
The von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
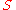of a mixture can be expressed in terms of the eigenvalues of or in terms of the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
and logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the density operator
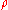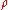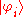. Since is a positive semi-definite operator, it has a spectral decomposition such that where are orthonormal vectors. Therefore the entropy of a quantum system with density matrix 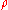is
Also it can be shown that
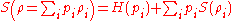
where
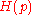is the Shannon entropy.This entropy can increase but never decrease with a measurement. The entropy of a pure state is zero, while that of a proper mixture always greater than zero. Therefore a pure state may be converted into a mixture by a measurement, but a proper mixture can never be converted into a pure state. Thus the act of measurement induces a fundamental irreversible
Irreversible
Irreversible may refer to:*Irreversible process, in thermodynamics, a process that is not reversible*Irréversible, a 2002 film*Irréversible , soundtrack to the film Irréversible...
change on the density matrix; this is analogous to the "collapse" of the state vector, or wavefunction collapse
Wavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
.
(A subsystem of a larger system can be turned from a mixed to a pure state, but only by increasing the von Neumann entropy elsewhere in the system. This is analogous to how the entropy of an object can be lowered by putting it in a refrigerator: The air outside the refrigerator's heat-exchanger warms up, gaining even more entropy than was lost by the object in the refrigerator. See second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
.)
Von Neumann equation
Just as the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
describes how pure states evolve in time, the von Neumann equation (also known as Liouville-von Neumann equation) describes how a density operator evolves in time (in fact, the two equations are equivalent, in the sense that either can be derived from the other.) The von Neumann equation states:
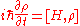
where the brackets denote a commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. Note that this equation is only true when the density operator is taken to be in the Schrödinger picture
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
even though this equation seems at first look to emulate the Heisenberg equation of motion:
where
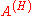is some 'Heisenberg' operator. Taking the density operator to be in the Schrödinger picture makes sense since it is composed of 'Schrödinger' kets and bras evolved in time as per the Schrödinger picture.If the Hamiltonian is time-independent, this differential equation can be solved to get
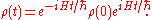
"Quantum Liouville", Moyal's equation
Under the Wigner mapWeyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
, the density matrix transforms into the Wigner function
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
,
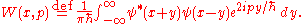
The equation for the time-evolution of the Wigner function is then the Wigner-transform of the above von Neumann equation,
where H(q,p) is the Hamiltonian, and { { •,• } } is the Moyal bracket
Moyal bracket
In physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
, the transform of the quantum commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
The evolution equation for the Wigner function is then analogous to that of its classical limit, the Liouville equation of classical physics
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
. In the limit of vanishing Planck's constant ħ, W(q,p,t) reduces to the classical Liouville probability density function in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
The classical Liouville equation can be solved using the method of characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
for partial differential equations, the characteristic equations being Hamilton's equations. The Moyal equation in quantum mechanics similarly admits formal solutions in terms of quantum characteristics
Method of quantum characteristics
In quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
, predicated on the ∗−product
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
of phase space, although, in actual practice, solution-seeking follows different methods.
Composite Systems
The joint density matrix of a composite system of two systems A and B is described by. Then the subsystems are described by their reduced density operator.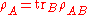 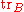is called partial tracePartial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
over system B.
If A and B are two distinct and independent systems then
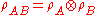which is a product state.C*-algebraic formulation of states
It is now generally accepted that the description of quantum mechanics in which all self-adjoint operators represent observables is untenable. For this reason, observables are identified to elements of an abstract C*-algebra A (that is one without a distinguished representation as an algebra of operators) and statesState (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
are positive linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on A. However, by using the GNS construction, we can recover Hilbert spaces which realize A as a subalgebra of operators.
Geometrically, a pure state on a C*-algebra A is a state which is an extreme point of the set of all states on A. By properties of the GNS construction these states correspond to irreducible representations of A.
The states of the C*-algebra of compact operators K(H) correspond exactly to the density operators and therefore the pure states of K(H) are exactly the pure states in the sense of quantum mechanics.
The C*-algebraic formulation can be seen to include both classical and quantum systems. When the system is classical, the algebra of observables become an abelian C*-algebra. In that case the states become probability measures, as noted in the introduction.
See also
- Fluctuation theoremFluctuation theoremThe fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
- Density functional theoryDensity functional theoryDensity functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
- Dynamic nuclear polarisationDynamic nuclear polarisationDynamic nuclear polarization results from transferring spin polarization from electrons to nuclei, thereby aligning the nuclear spins to the extent that electron spins are aligned. Note that the alignment of electron spins at a given magnetic field and temperature is described by the Boltzmann...
- Linear response functionLinear response functionA linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
- Green's function (many-body theory)Green's function (many-body theory)In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
- Lindblad equationLindblad equationIn quantum mechanics, the Kossakowski–Lindblad equation or master equation in the Lindblad form is the most general type of markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix \rho that is trace preserving and completely positive for any initial...
- Green–Kubo relations
- Purification of quantum statePurification of quantum stateIn quantum mechanics, especially quantum information, purification refers to the fact that every mixed state acting on finite dimensional Hilbert spaces can be viewed as the reduced state of some pure state....
- POVMPOVMIn functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
Generalized measurement of density states - Quantum logicQuantum logicIn quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
- Wigner quasi-probability distributionWigner quasi-probability distributionThe Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...