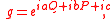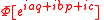Weyl quantization
Encyclopedia
In mathematics
and physics
, in the area of quantum mechanics
, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space
invertibly. A synonym is phase-space quantization.
The crucial correspondence map from phase-space functions to Hilbert space
operators underlying the method is called the Weyl transformation, (not to be confused with a different definition of the Weyl transformation), and was first detailed by Hermann Weyl
in 1927.
In some contrast to Weyl's original intentions in seeking a consistent quantization scheme, this map merely amounts to a change of representation. It need not connect "classical" with "quantum" quantities: the starting phase-space function may well depend on Planck's constant ħ. Indeed, in some familiar cases involving angular momentum, it does.
The inverse of this Weyl transformation is the Wigner map, which reverts from Hilbert space
to the phase-space representation, (cf. the Wigner quasi-probability distribution
, which is the Wigner map of the quantum density matrix
).
This invertible representation change then allows expressing quantum mechanics in phase space, as was appreciated in the 1940s by Groenewold
and Moyal
.
The Weyl transform of f is given by the following operator in Hilbert space, broadly analogous to a Dirac delta function
,
Here, the operators P and Q are taken to be the generators of a Lie algebra
, the Heisenberg algebra: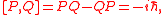
where ħ is the reduced Planck constant. A general element of the Heisenberg algebra may thus be written as aQ+bP+c .
The exponential map
of this element of the Lie algebra is then an element of the corresponding Lie group
,
the Heisenberg group. Given some particular group representation
Φ of the Heisenberg group, the quantity
denotes the element of the representation corresponding to the group element g.
This Weyl map may also be expressed in terms of the integral kernel matrix elements of the operator,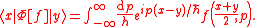
The inverse of the above Weyl map is the Wigner map, which
takes the operator Φ back to the original phase-space kernel function f ,
In general, the resulting function f depends on Planck's constant ħ, and may well describe quantum-mechanical processes, provided it is properly composed through the star product
, below.
For example, the Wigner map of the quantum angular-momentum-squared operator L2 is not just the classical angular momentum squared, but it further contains a term − 3ħ2/2, which accounts
for the nonvanishing angular momentum of the ground-state Bohr orbit.
(Hermitian) operators on some Hilbert space
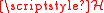 , such that their commutator, a central element of the group, amounts to the identity on that Hilbert space,
, such that their commutator, a central element of the group, amounts to the identity on that Hilbert space,

the quantum Canonical commutation relation. The Hilbert space may be taken to be the set of square integrable functions on the real number line (the plane waves), or a more bounded set, such as Schwartz space. Depending on the space involved, various results follow:
of a mathematical object is a family of the same kind of objects that depend on some parameter(s). The basic setup in deformation (quantization) theory is to start with an algebraic structure (say a Lie algebra
) and ask: Does there exist a one or more parameter(s) family of similar structures, such that for an initial value of the parameter(s) one gets the same structure (Lie algebra) one started with? E.g., one may define a noncommutative torus
as a deformation quantization through a ∗-product to implicitly address all convergence subtleties (usually not addressed in formal deformation quantization).
Insofar as the algebra of functions on a space determines the geometry of that space, the study of the star product leads to the study of a non-commutative geometry deformation of that space. In the context of the above flat phase-space example, the star product (Moyal product
, actually introduced by Groenewold in 1946), ∗ħ, of a pair of functions in f1,f2 ∈ C∞(ℜ2), is specified by
The star product is not commutative in general, but goes over to the ordinary commutative product of functions in the limit of ħ → 0. As such, it is said to define a deformation
of the commutative algebra of C∞(ℜ2).
For the Weyl-map example above, the ∗-product may be written in
terms of the Poisson bracket
as
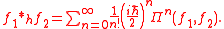
Here, Π is an operator defined such that its powers are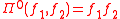
and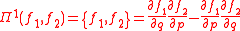
where {f1 , f2} is the Poisson bracket
. More generally,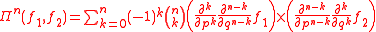
where is the binomial coefficient
is the binomial coefficient
.
This formula is predicated on coordinates in which the Poisson bivector is constant (plain flat Poisson brackets).
For the general formula on arbitrary Poisson manifold
s, cf. the Kontsevich quantization formula
.
Antisymmetrization of this ∗-product yields the Moyal bracket
, the proper quantum deformation of the Poisson bracket
,
and the phase-space isomorph of the quantum commutator
in the
more usual Hilbert-space formulation of quantum mechanics. As such, it provides
the cornerstone of the dynamical equations of observables in this phase-space formulation.
There results a complete phase-space representation of quantum mechanics, completely equivalent to the Hilbert-space operator representation, with star-multiplications paralleling operator multiplications isomorphically.
Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables Φ with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables such as the above f with the Wigner quasi-probability distribution
effectively serving as a measure.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the above Weyl map facilitates recognition of quantum mechanics as a deformation
(generalization) of classical mechanics, with deformation parameter ħ/S. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c; or the deformation of Newtonian gravity into General Relativity, with deformation parameter Schwarzschild-radius/characteristic-dimension.)
Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.
, or possibly a Poisson manifold
. Related structures include the Poisson–Lie groups and Kac–Moody algebra
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, in the area of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
invertibly. A synonym is phase-space quantization.
The crucial correspondence map from phase-space functions to Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
operators underlying the method is called the Weyl transformation, (not to be confused with a different definition of the Weyl transformation), and was first detailed by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in 1927.
In some contrast to Weyl's original intentions in seeking a consistent quantization scheme, this map merely amounts to a change of representation. It need not connect "classical" with "quantum" quantities: the starting phase-space function may well depend on Planck's constant ħ. Indeed, in some familiar cases involving angular momentum, it does.
The inverse of this Weyl transformation is the Wigner map, which reverts from Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
to the phase-space representation, (cf. the Wigner quasi-probability distribution
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
, which is the Wigner map of the quantum density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
).
This invertible representation change then allows expressing quantum mechanics in phase space, as was appreciated in the 1940s by Groenewold
Hilbrand J. Groenewold
Hilbrand Johannes Groenewold was a Dutch theoretical physicist who pioneered the largely operator-free formulation of quantum mechanics in phase space known as phase-space quantization....
and Moyal
José Enrique Moyal
José Enrique Moyal was a mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among other fields...
.
Example
The following illustrates the Weyl transformation on the simplest, two-dimensional Euclidean phase space. Let the coordinates on phase space be (q,p), and let f be a function defined everywhere on phase space.The Weyl transform of f is given by the following operator in Hilbert space, broadly analogous to a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
,

Here, the operators P and Q are taken to be the generators of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, the Heisenberg algebra:
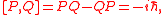
where ħ is the reduced Planck constant. A general element of the Heisenberg algebra may thus be written as aQ+bP+c .
The exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
of this element of the Lie algebra is then an element of the corresponding Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
,
the Heisenberg group. Given some particular group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
Φ of the Heisenberg group, the quantity
denotes the element of the representation corresponding to the group element g.
This Weyl map may also be expressed in terms of the integral kernel matrix elements of the operator,
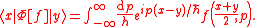
The inverse of the above Weyl map is the Wigner map, which
takes the operator Φ back to the original phase-space kernel function f ,

In general, the resulting function f depends on Planck's constant ħ, and may well describe quantum-mechanical processes, provided it is properly composed through the star product
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
, below.
For example, the Wigner map of the quantum angular-momentum-squared operator L2 is not just the classical angular momentum squared, but it further contains a term − 3ħ2/2, which accounts
for the nonvanishing angular momentum of the ground-state Bohr orbit.
Properties
Typically, the standard quantum-mechanical representation of the Heisenberg group is through its (Lie Algebra) generators: a pair of self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
(Hermitian) operators on some Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
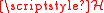 , such that their commutator, a central element of the group, amounts to the identity on that Hilbert space,
, such that their commutator, a central element of the group, amounts to the identity on that Hilbert space,
the quantum Canonical commutation relation. The Hilbert space may be taken to be the set of square integrable functions on the real number line (the plane waves), or a more bounded set, such as Schwartz space. Depending on the space involved, various results follow:
- If f is a real-valued functionReal-valued functionIn mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
, then its Weyl-map image Φ[f] is self-adjointSelf-adjointIn mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
.
- If f is an element of Schwartz space, then Φ[f] is trace-class.
- More generally, Φ[f] is a densely defined unbounded operatorUnbounded operatorIn mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
.
- For the standard representation of the Heisenberg group by square integrable functions, the map Φ[f] is one-to-one on the Schwartz space (as a subspace of the square-integrable functions).
Deformation quantization
Intuitively, a deformationDeformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of a mathematical object is a family of the same kind of objects that depend on some parameter(s). The basic setup in deformation (quantization) theory is to start with an algebraic structure (say a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
) and ask: Does there exist a one or more parameter(s) family of similar structures, such that for an initial value of the parameter(s) one gets the same structure (Lie algebra) one started with? E.g., one may define a noncommutative torus
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
as a deformation quantization through a ∗-product to implicitly address all convergence subtleties (usually not addressed in formal deformation quantization).
Insofar as the algebra of functions on a space determines the geometry of that space, the study of the star product leads to the study of a non-commutative geometry deformation of that space. In the context of the above flat phase-space example, the star product (Moyal product
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
, actually introduced by Groenewold in 1946), ∗ħ, of a pair of functions in f1,f2 ∈ C∞(ℜ2), is specified by
The star product is not commutative in general, but goes over to the ordinary commutative product of functions in the limit of ħ → 0. As such, it is said to define a deformation
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of the commutative algebra of C∞(ℜ2).
For the Weyl-map example above, the ∗-product may be written in
terms of the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
as
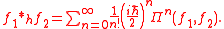
Here, Π is an operator defined such that its powers are
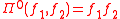
and
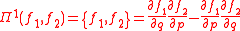
where {f1 , f2} is the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. More generally,
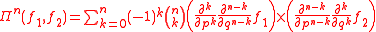
where
 is the binomial coefficient
is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
This formula is predicated on coordinates in which the Poisson bivector is constant (plain flat Poisson brackets).
For the general formula on arbitrary Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
s, cf. the Kontsevich quantization formula
Kontsevich quantization formula
In mathematics, the Kontsevich quantization formula describes how to construct an generalized ∗-product operator algebra from a given Poisson manifold. This operator algebra amounts to the deformation quantization of the Poisson algebra...
.
Antisymmetrization of this ∗-product yields the Moyal bracket
Moyal bracket
In physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
, the proper quantum deformation of the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
,
and the phase-space isomorph of the quantum commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
in the
more usual Hilbert-space formulation of quantum mechanics. As such, it provides
the cornerstone of the dynamical equations of observables in this phase-space formulation.
There results a complete phase-space representation of quantum mechanics, completely equivalent to the Hilbert-space operator representation, with star-multiplications paralleling operator multiplications isomorphically.
Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables Φ with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables such as the above f with the Wigner quasi-probability distribution
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
effectively serving as a measure.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the above Weyl map facilitates recognition of quantum mechanics as a deformation
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
(generalization) of classical mechanics, with deformation parameter ħ/S. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c; or the deformation of Newtonian gravity into General Relativity, with deformation parameter Schwarzschild-radius/characteristic-dimension.)
Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.
Generalizations
In more generality, Weyl quantization is studied in cases where the phase space is a symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, or possibly a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. Related structures include the Poisson–Lie groups and Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s.
See also
- Canonical commutation relation
- Heisenberg group
- Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
- Weyl algebra
- Wigner quasi-probability distributionWigner quasi-probability distributionThe Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
- Stone–von Neumann theoremStone–von Neumann theoremIn mathematics and in theoretical physics, the Stone–von Neumann theorem is any one of a number of different formulations of the uniqueness of the canonical commutation relations between position and momentum operators...