
Fubini-Study metric
Encyclopedia
In mathematics
, the Fubini–Study metric is a Kähler metric on projective Hilbert space
, that is, complex projective space
CPn endowed with a Hermitian form. This metric
was originally described in 1904 and 1905 by Guido Fubini
and Eduard Study
.
A Hermitian form in (the vector space) Cn+1 defines a unitary subgroup U(n+1) in GL(n+1,C). A Fubini–Study metric is determined up to homothety (overall scaling) by invariance under such a U(n+1) action; thus it is homogeneous. Equipped with a Fubini–Study metric, CPn is a symmetric space
. The particular normalization on the metric depends on the application. In Riemannian geometry
, one uses a normalization so that the Fubini-Study metric simply relates to the standard metric on the (2n+1)-sphere. In algebraic geometry
, one uses a normalization making CPn a Hodge manifold.
construction of complex projective space
.
Specifically, one may define CPn to be the space consisting of all complex lines in Cn+1, i.e., the quotient of Cn+1\{0} by the equivalence relation
relating all complex multiples of each point together. This agrees with the quotient by the diagonal group action
of the multiplicative group C* = C \ {0}:

This quotient realizes Cn+1\{0} as a complex line bundle
over the base space CPn. (In fact this is the so-called tautological bundle
over CPn.) A point of CPn is thus identified with an equivalence class of (n+1)-tuples [Z0,...,Zn] modulo nonzero complex rescaling; the Zi are called homogeneous coordinates
of the point.
Furthermore, one may realize this quotient in two steps: since multiplication by a nonzero complex scalar z = R eiθ can be uniquely thought of as the composition of a dilation by the modulus R followed by a counterclockwise rotation about the origin by an angle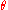 , the quotient Cn+1 → CPn splits into two pieces.
, the quotient Cn+1 → CPn splits into two pieces.

where step (a) is a quotient by the dilation Z ~ RZ for R ∈ R+, the multiplicative group of positive real numbers, and step (b) is a quotient by the rotations Z ~ eiθZ.
The result of the quotient in (a) is the real hypersphere S2n+1 defined by the equation |Z|2 = |Z0|2 + ... + |Zn|2 = 1. The quotient in (b) realizes CPn = S2n+1/S1, where S1 represents the group of rotations. This quotient is realized explicitly by the famous Hopf fibration S1 → S2n+1 → CPn, the fibers of which are among the great circles of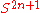 .
.
(or metric space
in general), care must be taken to ensure that the quotient space is endowed with a metric that is well-defined. For instance, if a group G acts on a Riemannian manifold (X,g), then in order for the orbit space X/G to possess an induced metric,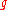 must be constant along G-orbits in the sense that for any element h ∈ G and pair of vector fields
must be constant along G-orbits in the sense that for any element h ∈ G and pair of vector fields  we must have g(Xh,Yh) = g(X,Y).
we must have g(Xh,Yh) = g(X,Y).
The standard Hermitian metric on Cn+1 is given in the standard basis by
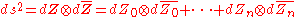
whose realification is the standard Euclidean metric on R2n+2. This metric is not invariant under the diagonal action of C*, so we are unable to directly push it down to CPn in the quotient. However, this metric is invariant under the diagonal action of S1 = U(1), the group of rotations. Therefore, step (b) in the above construction is possible once step (a) is accomplished.
The Fubini-Study metric is the metric induced on the quotient CPn = S2n+1/S1, where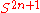 carries the so-called "round metric" endowed upon it by restriction of the standard Euclidean metric to the unit hypersphere.
carries the so-called "round metric" endowed upon it by restriction of the standard Euclidean metric to the unit hypersphere.

provided Z0 ≠ 0; specifically, zj = Zj/Z0. The (z1,…,zn) form an affine coordinate system for CPn in the coordinate patch U0 = {Z0 ≠ 0}. One can develop an affine coordinate system in any of the coordinate patches Ui = {Zi ≠ 0} by dividing instead by Zi in the obvious manner. The n+1 coordinate patches Ui cover CPn, and it is possible to give the metric explicitly in terms of the affine coordinates (z1,…,zn) on Ui. The coordinate derivatives define a frame of the holomorphic tangent bundle of CPn, in terms of which the Fubini–Study metric has Hermitian components
of the holomorphic tangent bundle of CPn, in terms of which the Fubini–Study metric has Hermitian components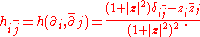
where |z|2 = z12+...+zn2. That is, the Hermitian matrix of the Fubini-Study metric in this frame is
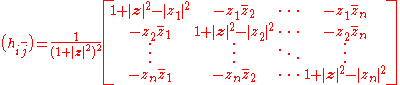
Note that each matrix element is unitary-invariant: the diagonal action will leave this matrix unchanged.
will leave this matrix unchanged.
Accordingly, the line element is given by
In this last expression, the summation convention is used to sum over Latin indices i,j that range from 1 to n.
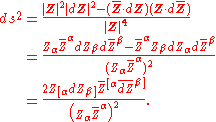
Here the summation convention is used to sum over Greek indices α β ranging from 0 to n, and in the last equality the standard notation for the skew part of a tensor is used:
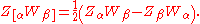
Now, this expression for ds2 apparently defines a tensor on the total space of the tautological bundle Cn+1\{0}. It is to be understood properly as a tensor on CPn by pulling it back along a holomorphic section σ of the tautological bundle of CPn. It remains then to verify that the value of the pullback is independent of the choice of section: this can be done by a direct calculation.
The Kähler form of this metric is, up to an overall constant normalization,
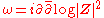
the pullback of which is clearly independent of the choice of holomorphic section. The quantity log|Z|2 is the Kähler scalar of CPn.
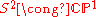 given by stereographic projection
given by stereographic projection
. This leads to the "special" Hopf fibration S1 → S3 → S2. When the Fubini-Study metric is written in coordinates on CP1, its restriction to the real tangent bundle yields an expression of the ordinary "round metric" of radius 1/2 (and Gaussian curvature
4) on S2.
Namely, if z = x + iy is the standard affine coordinate chart on the Riemann sphere
CP1 and x = r cosθ, y = r sinθ are polar coordinates on C, then a routine computation shows
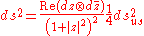
where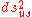 is the round metric on the unit 2-sphere. Here φ, θ are "mathematician's spherical coordinates" on S2 coming from the stereographic projection r tan(φ/2) = 1, tanθ = y/x. (Many physics references interchange the roles of φ and θ.)
is the round metric on the unit 2-sphere. Here φ, θ are "mathematician's spherical coordinates" on S2 coming from the stereographic projection r tan(φ/2) = 1, tanθ = y/x. (Many physics references interchange the roles of φ and θ.)
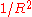 ). However, for n > 1, the Fubini-Study metric does not have constant curvature. Its sectional curvature is instead by the equation
). However, for n > 1, the Fubini-Study metric does not have constant curvature. Its sectional curvature is instead by the equation

where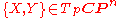 is an orthonormal basis of the 2-plane σ, J : TCPn → TCPn is the complex structure
is an orthonormal basis of the 2-plane σ, J : TCPn → TCPn is the complex structure
on CPn, and is the Fubini-Study metric.
is the Fubini-Study metric.
A consequence of this formula is that the sectional curvature satisfies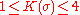 for all 2-planes
for all 2-planes  . The maximum sectional curvature (4) is attained at a holomorphic 2-plane — one for which J(σ) ⊂ σ — while the minimum sectional curvature (1) is attained at a 2-plane for which J(σ) is orthogonal to σ. For this reason, the Fubini-Study metric is often said to have "constant holomorphic sectional curvature" equal to 4.
. The maximum sectional curvature (4) is attained at a holomorphic 2-plane — one for which J(σ) ⊂ σ — while the minimum sectional curvature (1) is attained at a 2-plane for which J(σ) is orthogonal to σ. For this reason, the Fubini-Study metric is often said to have "constant holomorphic sectional curvature" equal to 4.
This makes CPn a (non-strict) quarter pinched manifold; a celebrated theorem shows that a strictly quarter-pinched simply connected n-manifold must be homeomorphic to a sphere.
The Fubini-Study metric is also an Einstein metric in that it is proportional to its own Ricci tensor: there exists a constant λ such that for all i,j we have
 .
.
This implies, among other things, that the Fubini-Study metric remains unchanged up to a scalar multiple under the Ricci flow
. It also makes CPn indispensable to the theory of general relativity
, where it serves as a nontrivial solution to the vacuum Einstein equations.
commonly used in quantum mechanics
, or the notation of projective varieties of algebraic geometry
. To explicitly equate these two languages, let

where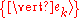 is a set of orthonormal basis vectors for Hilbert space
is a set of orthonormal basis vectors for Hilbert space
, the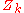 are complex numbers, and
are complex numbers, and 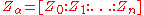 is the standard notation for a point in the projective space
is the standard notation for a point in the projective space 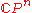 in homogeneous coordinates
in homogeneous coordinates
. Then, given two points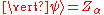 and
and 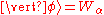 in the space, the distance between them is
in the space, the distance between them is

or, equivalently, in projective variety notation,
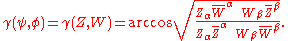
Here, is the complex conjugate
is the complex conjugate
of . The appearance of
. The appearance of  in the denominator is a reminder that
in the denominator is a reminder that  and likewise
and likewise  were not normalized to unit length; thus the normalization is made explicit here. In Hilbert space, the metric can be rather trivially interpreted as the angle between two vectors; thus it is occasionally called the quantum angle. The angle is real-valued, and runs from zero to
were not normalized to unit length; thus the normalization is made explicit here. In Hilbert space, the metric can be rather trivially interpreted as the angle between two vectors; thus it is occasionally called the quantum angle. The angle is real-valued, and runs from zero to 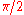 .
.
The infinitesimal form of this metric may be quickly obtained by taking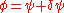 , or equivalently,
, or equivalently,  to obtain
to obtain
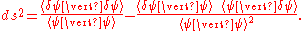
In the context of quantum mechanics
, CP1 is called the Bloch sphere
; the Fubini–Study metric is the natural metric
for the geometrization of quantum mechanics. Much of the peculiar behaviour of quantum mechanics, including quantum entanglement
and the Berry phase effect, can be attributed to the peculiarities of the Fubini–Study metric.
. That is, if is a separable state, so that it can be written as
is a separable state, so that it can be written as  , then the metric is the sum of the metric on the subspaces:
, then the metric is the sum of the metric on the subspaces:
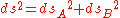
where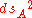 and
and 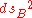 are the metrics, respectively, on the subspaces A and B.
are the metrics, respectively, on the subspaces A and B.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fubini–Study metric is a Kähler metric on projective Hilbert space
Projective Hilbert space
In mathematics and the foundations of quantum mechanics, the projective Hilbert space P of a complex Hilbert space H is the set of equivalence classes of vectors v in H, with v ≠ 0, for the relation given by...
, that is, complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
CPn endowed with a Hermitian form. This metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
was originally described in 1904 and 1905 by Guido Fubini
Guido Fubini
Guido Fubini was an Italian mathematician, known for Fubini's theorem and the Fubini–Study metric.Born in Venice, he was steered towards mathematics at an early age by his teachers and his father, who was himself a teacher of mathematics...
and Eduard Study
Eduard Study
Eduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
.
A Hermitian form in (the vector space) Cn+1 defines a unitary subgroup U(n+1) in GL(n+1,C). A Fubini–Study metric is determined up to homothety (overall scaling) by invariance under such a U(n+1) action; thus it is homogeneous. Equipped with a Fubini–Study metric, CPn is a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
. The particular normalization on the metric depends on the application. In Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, one uses a normalization so that the Fubini-Study metric simply relates to the standard metric on the (2n+1)-sphere. In algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, one uses a normalization making CPn a Hodge manifold.
Construction
The Fubini-Study metric arises naturally in the quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
construction of complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
.
Specifically, one may define CPn to be the space consisting of all complex lines in Cn+1, i.e., the quotient of Cn+1\{0} by the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
relating all complex multiples of each point together. This agrees with the quotient by the diagonal group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the multiplicative group C* = C \ {0}:

This quotient realizes Cn+1\{0} as a complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
over the base space CPn. (In fact this is the so-called tautological bundle
Tautological bundle
In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
over CPn.) A point of CPn is thus identified with an equivalence class of (n+1)-tuples [Z0,...,Zn] modulo nonzero complex rescaling; the Zi are called homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
of the point.
Furthermore, one may realize this quotient in two steps: since multiplication by a nonzero complex scalar z = R eiθ can be uniquely thought of as the composition of a dilation by the modulus R followed by a counterclockwise rotation about the origin by an angle
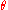 , the quotient Cn+1 → CPn splits into two pieces.
, the quotient Cn+1 → CPn splits into two pieces.
where step (a) is a quotient by the dilation Z ~ RZ for R ∈ R+, the multiplicative group of positive real numbers, and step (b) is a quotient by the rotations Z ~ eiθZ.
The result of the quotient in (a) is the real hypersphere S2n+1 defined by the equation |Z|2 = |Z0|2 + ... + |Zn|2 = 1. The quotient in (b) realizes CPn = S2n+1/S1, where S1 represents the group of rotations. This quotient is realized explicitly by the famous Hopf fibration S1 → S2n+1 → CPn, the fibers of which are among the great circles of
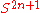 .
.As a metric quotient
When a quotient is taken of a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(or metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
in general), care must be taken to ensure that the quotient space is endowed with a metric that is well-defined. For instance, if a group G acts on a Riemannian manifold (X,g), then in order for the orbit space X/G to possess an induced metric,
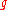 must be constant along G-orbits in the sense that for any element h ∈ G and pair of vector fields
must be constant along G-orbits in the sense that for any element h ∈ G and pair of vector fields  we must have g(Xh,Yh) = g(X,Y).
we must have g(Xh,Yh) = g(X,Y).The standard Hermitian metric on Cn+1 is given in the standard basis by
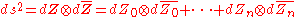
whose realification is the standard Euclidean metric on R2n+2. This metric is not invariant under the diagonal action of C*, so we are unable to directly push it down to CPn in the quotient. However, this metric is invariant under the diagonal action of S1 = U(1), the group of rotations. Therefore, step (b) in the above construction is possible once step (a) is accomplished.
The Fubini-Study metric is the metric induced on the quotient CPn = S2n+1/S1, where
 carries the so-called "round metric" endowed upon it by restriction of the standard Euclidean metric to the unit hypersphere.
carries the so-called "round metric" endowed upon it by restriction of the standard Euclidean metric to the unit hypersphere.In local affine coordinates
Corresponding to a point in CPn with homogeneous coordinates (Z0,...,Zn), there is a unique set of n coordinates (z1,…,zn) such that
provided Z0 ≠ 0; specifically, zj = Zj/Z0. The (z1,…,zn) form an affine coordinate system for CPn in the coordinate patch U0 = {Z0 ≠ 0}. One can develop an affine coordinate system in any of the coordinate patches Ui = {Zi ≠ 0} by dividing instead by Zi in the obvious manner. The n+1 coordinate patches Ui cover CPn, and it is possible to give the metric explicitly in terms of the affine coordinates (z1,…,zn) on Ui. The coordinate derivatives define a frame
 of the holomorphic tangent bundle of CPn, in terms of which the Fubini–Study metric has Hermitian components
of the holomorphic tangent bundle of CPn, in terms of which the Fubini–Study metric has Hermitian components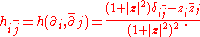
where |z|2 = z12+...+zn2. That is, the Hermitian matrix of the Fubini-Study metric in this frame is
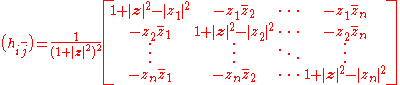
Note that each matrix element is unitary-invariant: the diagonal action
 will leave this matrix unchanged.
will leave this matrix unchanged.Accordingly, the line element is given by

In this last expression, the summation convention is used to sum over Latin indices i,j that range from 1 to n.
Homogeneous coordinates
An expression is also possible in the homogeneous coordinates Z = [Z0,...,Zn]. Formally, subject to suitably interpreting the expressions involved, one has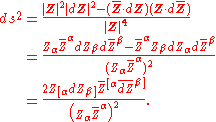
Here the summation convention is used to sum over Greek indices α β ranging from 0 to n, and in the last equality the standard notation for the skew part of a tensor is used:
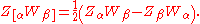
Now, this expression for ds2 apparently defines a tensor on the total space of the tautological bundle Cn+1\{0}. It is to be understood properly as a tensor on CPn by pulling it back along a holomorphic section σ of the tautological bundle of CPn. It remains then to verify that the value of the pullback is independent of the choice of section: this can be done by a direct calculation.
The Kähler form of this metric is, up to an overall constant normalization,
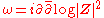
the pullback of which is clearly independent of the choice of holomorphic section. The quantity log|Z|2 is the Kähler scalar of CPn.
The n = 1 case
When n = 1, there is a diffeomorphism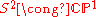 given by stereographic projection
given by stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. This leads to the "special" Hopf fibration S1 → S3 → S2. When the Fubini-Study metric is written in coordinates on CP1, its restriction to the real tangent bundle yields an expression of the ordinary "round metric" of radius 1/2 (and Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
4) on S2.
Namely, if z = x + iy is the standard affine coordinate chart on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
CP1 and x = r cosθ, y = r sinθ are polar coordinates on C, then a routine computation shows
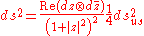
where
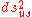 is the round metric on the unit 2-sphere. Here φ, θ are "mathematician's spherical coordinates" on S2 coming from the stereographic projection r tan(φ/2) = 1, tanθ = y/x. (Many physics references interchange the roles of φ and θ.)
is the round metric on the unit 2-sphere. Here φ, θ are "mathematician's spherical coordinates" on S2 coming from the stereographic projection r tan(φ/2) = 1, tanθ = y/x. (Many physics references interchange the roles of φ and θ.)Curvature properties
In the n = 1 special case, the Fubini-Study metric has constant scalar curvature identically equal to 4, according to the equivalence with the 2-sphere's round metric (which given a radius R has scalar curvature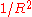 ). However, for n > 1, the Fubini-Study metric does not have constant curvature. Its sectional curvature is instead by the equation
). However, for n > 1, the Fubini-Study metric does not have constant curvature. Its sectional curvature is instead by the equation
where
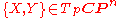 is an orthonormal basis of the 2-plane σ, J : TCPn → TCPn is the complex structure
is an orthonormal basis of the 2-plane σ, J : TCPn → TCPn is the complex structureLinear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
on CPn, and
 is the Fubini-Study metric.
is the Fubini-Study metric.A consequence of this formula is that the sectional curvature satisfies
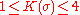 for all 2-planes
for all 2-planes  . The maximum sectional curvature (4) is attained at a holomorphic 2-plane — one for which J(σ) ⊂ σ — while the minimum sectional curvature (1) is attained at a 2-plane for which J(σ) is orthogonal to σ. For this reason, the Fubini-Study metric is often said to have "constant holomorphic sectional curvature" equal to 4.
. The maximum sectional curvature (4) is attained at a holomorphic 2-plane — one for which J(σ) ⊂ σ — while the minimum sectional curvature (1) is attained at a 2-plane for which J(σ) is orthogonal to σ. For this reason, the Fubini-Study metric is often said to have "constant holomorphic sectional curvature" equal to 4.This makes CPn a (non-strict) quarter pinched manifold; a celebrated theorem shows that a strictly quarter-pinched simply connected n-manifold must be homeomorphic to a sphere.
The Fubini-Study metric is also an Einstein metric in that it is proportional to its own Ricci tensor: there exists a constant λ such that for all i,j we have
 .
.This implies, among other things, that the Fubini-Study metric remains unchanged up to a scalar multiple under the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
. It also makes CPn indispensable to the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, where it serves as a nontrivial solution to the vacuum Einstein equations.
In quantum mechanics
The Fubini-Study metric may be defined either using the bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
commonly used in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, or the notation of projective varieties of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. To explicitly equate these two languages, let

where
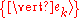 is a set of orthonormal basis vectors for Hilbert space
is a set of orthonormal basis vectors for Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, the
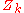 are complex numbers, and
are complex numbers, and 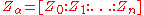 is the standard notation for a point in the projective space
is the standard notation for a point in the projective space 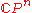 in homogeneous coordinates
in homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. Then, given two points
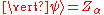 and
and 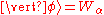 in the space, the distance between them is
in the space, the distance between them is
or, equivalently, in projective variety notation,
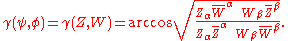
Here,
 is the complex conjugate
is the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of
 . The appearance of
. The appearance of  in the denominator is a reminder that
in the denominator is a reminder that  and likewise
and likewise  were not normalized to unit length; thus the normalization is made explicit here. In Hilbert space, the metric can be rather trivially interpreted as the angle between two vectors; thus it is occasionally called the quantum angle. The angle is real-valued, and runs from zero to
were not normalized to unit length; thus the normalization is made explicit here. In Hilbert space, the metric can be rather trivially interpreted as the angle between two vectors; thus it is occasionally called the quantum angle. The angle is real-valued, and runs from zero to 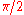 .
.The infinitesimal form of this metric may be quickly obtained by taking
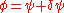 , or equivalently,
, or equivalently,  to obtain
to obtain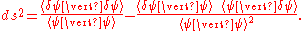
In the context of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, CP1 is called the Bloch sphere
Bloch sphere
In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
; the Fubini–Study metric is the natural metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
for the geometrization of quantum mechanics. Much of the peculiar behaviour of quantum mechanics, including quantum entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
and the Berry phase effect, can be attributed to the peculiarities of the Fubini–Study metric.
Product metric
The common notions of separability apply for the Fubini–Study metric. More precisely, the metric is separable on the natural product of projective spaces, the Segre embeddingSegre embedding
In mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
. That is, if
 is a separable state, so that it can be written as
is a separable state, so that it can be written as  , then the metric is the sum of the metric on the subspaces:
, then the metric is the sum of the metric on the subspaces: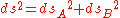
where
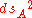 and
and 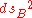 are the metrics, respectively, on the subspaces A and B.
are the metrics, respectively, on the subspaces A and B.

