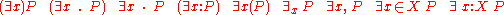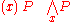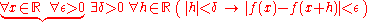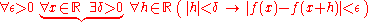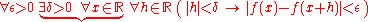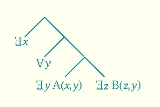
Quantification
Encyclopedia
Quantification has several distinct senses. In mathematics
and empirical science, it is the act of counting
and measuring that maps human sense observation
s and experience
s into members of some set of number
s. Quantification in this sense is fundamental to the scientific method
.
In logic
, quantification is the binding of a variable ranging over a domain of discourse
. The variable thereby becomes bound by an operator called a quantifier. Academic discussion of quantification refers more often to this meaning of the term than the preceding one.
In grammar, a quantifier is a type of determiner
, such as all or many, that indicates quantity. These items have been argued to correspond to logical quantifiers at the semantic level.
The words in italics are quantifiers.
There exists no simple way of reformulating any one of these expressions as a conjunction or disjunction of sentences, each a simple predicate of an individual such as That wine glass was chipped. These examples also suggest that the construction of quantified expressions in natural language can be syntactically very complicated. Fortunately, for mathematical assertions, the quantification process is syntactically more straightforward.
The study of quantification in natural languages is much more difficult than the corresponding problem for formal languages. This comes in part from the fact that the grammatical structure of natural language sentences may conceal the logical structure. Moreover, mathematical conventions strictly specify the range of validity for formal language quantifiers; for natural language, specifying the range of validity requires dealing with non-trivial semantic problems. For example the sentence ″Someone gets mugged in New York every 10 minutes″ does not identify whether it is the same person getting mugged every 10 minutes.
Montague grammar
gives a novel formal semantics of natural languages. Its proponents argue that it provides a much more natural formal rendering of natural language than the traditional treatments of Frege
, Russell
and Quine
.
and logic
, quantification is a construct that specifies the quantity of specimens in the domain of discourse
that apply to (or satisfy) an open formula. For example, in arithmetic, it allows the expression of the statement that every natural number has a successor. A language element which generates a quantification is called a quantifier. The resulting expression is a quantified expression; and the expression is said to be quantified over the predicate or function expression whose free variable
is bound by the quantifier. Quantification is used in both natural language
s and formal language
s. Examples of quantifiers in English are for all, for some, many, few, a lot, and no. In formal languages, quantification is a formula constructor that produces new formulas from old ones. The semantics
of the language specifies how the constructor is interpreted as an extent of validity.
The two fundamental kinds of quantification in predicate logic are universal quantification
and existential quantification
. The traditional symbol for the universal quantifier "all" is "∀", an inverted letter "A
", and for the existential quantifier
"exists" is "∃", a rotated letter "E
". These quantifiers have been generalized beginning with the work of Mostowski and Lindström. See generalized quantifier
and Lindström quantifier
for further details.
This has the appearance of an infinite conjunction
of propositions. From the point of view of formal language
s this is immediately a problem, since syntax
rules are expected to generate finite objects. The example above is fortunate in that there is a procedure
to generate all the conjuncts. However, if an assertion were to be made about every irrational number
, there would be no way to enumerate all the conjuncts, since irrationals cannot be enumerated. A succinct formulation which avoids these problems uses universal quantification:
A similar analysis applies to the disjunction,
which can be rephrased using existential quantification:
It is possible to devise abstract algebra
s whose models
include formal language
s with quantification, but progress has been slow and interest in such algebra has been limited. Three approaches have been devised to date:
", which stands for the word "all"; in other schools, a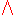
is used instead. The corresponding symbol for the existential quantifier is "∃", a rotated letter "E
", which stands for the word "exists". Other schools use the symbol
instead.
Correspondingly, quantified expressions are constructed as follows,
for a formula P. Variant notations include, for set X and set members x:
All of these variations also apply to universal quantification.
Other variations for the universal quantifier are
Some versions of the notation explicitly mention the range of quantification. The range of quantification must always be specified; for a given mathematical theory, this can be done in several ways:
One can use any variable as a quantified variable in place of any other, under certain restrictions in which variable capture does not occur. Even if the notation uses typed variables, variables of that type may be used.
Informally or in natural language, the "∀x" or "∃x" might appear after or in the middle of P(x). Formally, however, the phrase that introduces the dummy variable is placed in front.
Mathematical formulas mix symbolic expressions for quantifiers, with natural language quantifiers such as
Keywords for uniqueness quantification
include:
Further, x may be replaced by a pronoun
. For example,
terms as
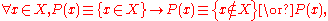
which equivalently reads "if x is in X, then P(x) is true." If x is not in X, then P(x) is indeterminate. Note that the truth of the expression requires only that x be in X, so it can be any x in X, independent of P(x), whereas the falsity of the expression, or the truth of
additionally requires that x be such that P(x) evaluates to false; this is the reason behind calling x a "bound variable." This last expression can thus be read as "for some x in X, P(x) is false," or "there exists an x in X such that P(x) is false." So, we now have the equivalent Boolean expression for the existential proposition:
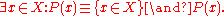
Thus, together with negation, only one of either the universal or existential quantifier is needed to perform both tasks:
which shows that to disprove a "for all x" proposition, one needs no more than to find an x for which the predicate is false. Similarly,
to disprove a "there exists an x" proposition, one needs to show that the predicate is false for all x.
This is clearly true; it just asserts that every natural number has a square. The meaning of the assertion in which the quantifiers are turned around is different:
This is clearly false; it asserts that there is a single natural number s that is at once the square of every natural number. This is because the syntax directs that any newly introduced variable cannot be a function of subsequently introduced variables.
This illustrates that the order of quantifiers is critical to meaning.
A less trivial example is the important concept of uniform continuity
from analysis
, which differs from the more familiar concept of pointwise continuity
only by an exchange in the positions of two quantifiers.
To illustrate this, let f be a real-valued function on R.
interchanging the universal quantifiers over the braces, this is the same as
Thus, it is implied that the particular value chosen for δ can only be a function of ε and x, the variables that precede it; whereas in
by interchanging the existential and universal quantifiers over the braces in A', δ is asserted to be independent of x.
Ambiguity is avoided with the quantifiers in front:
. Expository conventions often reserve some variable names such as "n" for natural numbers and "x" for real numbers, although relying exclusively on naming conventions cannot work in general since ranges of variables can change in the course of a mathematical argument.
A more natural way to restrict the domain of discourse uses guarded quantification. For example, the guarded quantification
means
In some mathematical theories a single domain of
discourse fixed in advance is assumed. For example, in Zermelo–Fraenkel set theory
, variables range over all sets. In this case, guarded quantifiers can be used to mimic a smaller range of quantification. Thus in the example
above to express
in Zermelo–Fraenkel set theory, it can be said
where N is the set of all natural numbers.
to study the meaning of expressions in a formal language. It has three elements: A mathematical specification of a class of objects via syntax
, a mathematical specification of various semantic domains and the relation between the two, which is usually expressed as a function from syntactic objects to semantic ones. This article only addresses the issue of how quantifier elements are interpreted.
Given a model theoretical
logical framework, the syntax of a formula can be given by a syntax tree. Quantifiers have scope and a variable x is free if it is not within the scope of a quantification for that variable. Thus in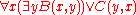
the occurrence of both x and y in C(y,x) is free.
An interpretation for first-order predicate calculus assumes as given
a domain of individuals X. A formula A whose free variables
are x1, ..., xn is interpreted as a
boolean-valued function F(v1, ...,
vn) of n arguments, where each argument ranges
over the domain X. Boolean-valued means that the function assumes one of the values T (interpreted as truth) or F (interpreted as falsehood). The interpretation of the formula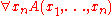
is the function G of n-1 arguments such that G(v1, ...,vn-1) = T if and only if F(v1, ..., vn-1, w) = T for every w in X. If F(v1, ..., vn-1, w) = F for at least one value of w, then G(v1, ...,vn-1) = F. Similarly the interpretation of the formula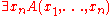
is the function H of n-1 arguments such that H(v1, ...,vn-1) = T if and only if F(v1, ...,vn-1, w) = T for at least one w and H(v1, ..., vn-1) = F otherwise.
The semantics for uniqueness quantification
requires first-order predicate calculus with equality. This means there is given a distinguished two-placed predicate "="; the semantics is also modified accordingly so that "=" is always interpreted as the two-place equality relation on X. The interpretation of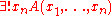
then is the function of n-1 arguments, which is the logical and of the interpretations of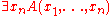
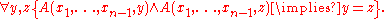
One possible interpretation mechanism can be obtained as follows: Suppose that in addition to a semantic domain X, we have given a probability measure
P defined on X and cutoff numbers 0 < a ≤ b ≤ 1. If A is a formula with free variables x1,...,xn whose interpretation is
the function F of variables v1,...,vn
then the interpretation of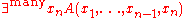
is the function of v1,...,vn-1 which is T if and only if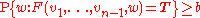
and F otherwise. Similarly, the interpretation of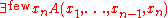
is the function of v1,...,vn-1 which is F if and only if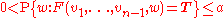
and T otherwise. See Fubini's theorem
for more discussion of the measurability of the interpretation functions.
) and read "those". For example: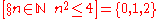
is read "those n in N such that n2 ≤ 4 are in {0,1,2}." The same construct is expressible in set-builder notation
:
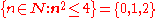
treats quantification in a manner that is closer to natural language, and also less suited to formal analysis. Aristotelian logic treated All, Some and No in the 1st century BC, in an account also touching on the alethic modalities.
Gottlob Frege
, in his 1879 Begriffsschrift
, was the first to employ a quantifier to bind a variable ranging over a domain of discourse
and appearing in predicates. He would universally quantify a variable (or relation) by writing the variable over a dimple in an otherwise straight line appearing in his diagrammatic formulas. Frege did not devise an explicit notation for existential quantification, instead employing his equivalent of ~∀x~, or contraposition
. Frege's treatment of quantification went largely unremarked until Bertrand Russell
's 1903 Principles of Mathematics.
In work that culminated in Peirce (1885), Charles Sanders Peirce and his student Oscar Howard Mitchell independently invented universal and existential quantifiers, and bound variables. Peirce and Mitchell wrote Πx and Σx where we now write ∀x and ∃x. Peirce's notation can be found in the writings of Ernst Schröder
, Leopold Loewenheim, Thoralf Skolem
, and Polish logicians into the 1950s. Most notably, it is the notation of Kurt Gödel
's landmark 1930 paper on the completeness
of first-order logic
, and 1931 paper on the incompleteness of Peano arithmetic.
Peirce's approach to quantification also influenced William Ernest Johnson
and Giuseppe Peano
, who invented yet another notation, namely (x) for the universal quantification of x and (in 1897) ∃x for the existential quantification of x. Hence for decades, the canonical notation in philosophy and mathematical logic was (x)P to express "all individuals in the domain of discourse have the property P," and "(∃x)P" for "there exists at least one individual in the domain of discourse having the property P." Peano, who was much better known than Peirce, in effect diffused the latter's thinking throughout Europe. Peano's notation was adopted by the Principia Mathematica
of Whitehead
and Russell
, Quine
, and Alonzo Church
. In 1935, Gentzen introduced the ∀ symbol, by analogy with Peano's ∃ symbol. ∀ did not become canonical until the 1960s.
Around 1895, Peirce began developing his existential graph
s, whose variables can be seen as tacitly quantified. Whether the shallowest instance of a variable is even or odd determines whether that variable's quantification is universal or existential. (Shallowness is the contrary of depth, which is determined by the nesting of negations.) Peirce's graphical logic has attracted some attention in recent years by those researching heterogeneous reasoning and diagrammatic inference
.
s can be gleaned from the following comments: "these are mere facts, but they are quantitative facts and the basis of science." It seems to be held as universally true that "the foundation of quantification is measurement." There is little doubt that "quantification provided a basis for the objectivity of science." In ancient times, "musicians and artists...rejected quantification, but merchants, by definition, quantified their affairs, in order to survive, made them visible on parchment and paper." Any reasonable "comparison between Aristotle and Galileo shows clearly that there can be no unique lawfulness discovered without detailed quantification." Even today, "universities use imperfect instruments called 'exams' to indirectly quantify something they call knowledge." This meaning of quantification comes under the heading of pragmatics
.
In some instances in the natural sciences a seemingly intangible concept may be quantified by creating a scale—for example, a pain scale
in medical research, or a discomfort scale at the intersection of meteorology
and human physiology
such as the heat index
measuring the combined perceived effect of heat and humidity
, or the wind chill factor measuring the combined perceived effects of cold and wind.
, quantification is an integral part of economics
and psychology
. Both disciplines gather data—economics by empirical observation and psychology by experimentation, and both use statistical techniques
such as regression analysis
to draw conclusions from it.
In some instances a seemingly intangible property may be quantified by asking subjects to rate something on a scale
—for example, a happiness scale or a quality of life scale
—or by the construction of a scale by the researcher, as with the index of economic freedom
. In other cases, an unobservable variable may be quantified by replacing it with a proxy variable
with which it is highly correlated—for example, per capita gross domestic product
is often used as a proxy for standard of living
or quality of life
.
Frequently in the use of regression, the presence or absence of a trait is quantified by employing a dummy variable, which takes on the value 1 in the presence of the trait or the value 0 in the absence of the trait.
Quantitative linguistics
is an area of linguistics
that relies on quantification. For example, indices of grammaticalization of morpheme
s, such as phonological
shortness, dependence on surroundings, and fusion with the verb, have been developed and found to be significantly correlated across languages with stage of evolution of function of the morpheme.
s from each other. Hard sciences are often considered to be more scientific, rigorous, or accurate. In some social sciences
such as sociology
, specific accurate data are difficult to obtain, either because laboratory conditions are not present or because the issues involved are conceptual but not directly quantifiable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and empirical science, it is the act of counting
Counting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
and measuring that maps human sense observation
Observation
Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
s and experience
Experience
Experience as a general concept comprises knowledge of or skill in or observation of some thing or some event gained through involvement in or exposure to that thing or event....
s into members of some set of number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s. Quantification in this sense is fundamental to the scientific method
Scientific method
Scientific method refers to a body of techniques for investigating phenomena, acquiring new knowledge, or correcting and integrating previous knowledge. To be termed scientific, a method of inquiry must be based on gathering empirical and measurable evidence subject to specific principles of...
.
In logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, quantification is the binding of a variable ranging over a domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
. The variable thereby becomes bound by an operator called a quantifier. Academic discussion of quantification refers more often to this meaning of the term than the preceding one.
In grammar, a quantifier is a type of determiner
Determiner (class)
A determiner is a noun-modifier that expresses the reference of a noun or noun-phrase in the context, rather than attributes expressed by adjectives...
, such as all or many, that indicates quantity. These items have been argued to correspond to logical quantifiers at the semantic level.
Natural language
All known human languages make use of quantification (Wiese 2004). For example, in English:- Every glass in my recent order was chipped.
- Some of the people standing across the river have white armbands.
- Most of the people I talked to didn't have a clue who the candidates were.
- A lot of people are smart.
The words in italics are quantifiers.
There exists no simple way of reformulating any one of these expressions as a conjunction or disjunction of sentences, each a simple predicate of an individual such as That wine glass was chipped. These examples also suggest that the construction of quantified expressions in natural language can be syntactically very complicated. Fortunately, for mathematical assertions, the quantification process is syntactically more straightforward.
The study of quantification in natural languages is much more difficult than the corresponding problem for formal languages. This comes in part from the fact that the grammatical structure of natural language sentences may conceal the logical structure. Moreover, mathematical conventions strictly specify the range of validity for formal language quantifiers; for natural language, specifying the range of validity requires dealing with non-trivial semantic problems. For example the sentence ″Someone gets mugged in New York every 10 minutes″ does not identify whether it is the same person getting mugged every 10 minutes.
Montague grammar
Montague grammar
Montague grammar is an approach to natural language semantics, named after American logician Richard Montague. The Montague grammar is based on formal logic, especially higher order predicate logic and lambda calculus, and makes use of the notions of intensional logic, via Kripke models...
gives a novel formal semantics of natural languages. Its proponents argue that it provides a much more natural formal rendering of natural language than the traditional treatments of Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
and Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
.
Logic
In languageLanguage
Language may refer either to the specifically human capacity for acquiring and using complex systems of communication, or to a specific instance of such a system of complex communication...
and logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, quantification is a construct that specifies the quantity of specimens in the domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
that apply to (or satisfy) an open formula. For example, in arithmetic, it allows the expression of the statement that every natural number has a successor. A language element which generates a quantification is called a quantifier. The resulting expression is a quantified expression; and the expression is said to be quantified over the predicate or function expression whose free variable
Free variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
is bound by the quantifier. Quantification is used in both natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
s and formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s. Examples of quantifiers in English are for all, for some, many, few, a lot, and no. In formal languages, quantification is a formula constructor that produces new formulas from old ones. The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of the language specifies how the constructor is interpreted as an extent of validity.
The two fundamental kinds of quantification in predicate logic are universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
and existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
. The traditional symbol for the universal quantifier "all" is "∀", an inverted letter "A
A
A is the first letter and a vowel in the basic modern Latin alphabet. It is similar to the Ancient Greek letter Alpha, from which it derives.- Origins :...
", and for the existential quantifier
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
"exists" is "∃", a rotated letter "E
E
E is the fifth letter and a vowel in the basic modern Latin alphabet. It is the most commonly used letter in the Czech, Danish, Dutch, English, French, German, Hungarian, Latin, Norwegian, Spanish, and Swedish languages.-History:...
". These quantifiers have been generalized beginning with the work of Mostowski and Lindström. See generalized quantifier
Generalized quantifier
In linguistic semantics, a generalized quantifier is an expression that denotes a property of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrases, also called determiner phrases, in short: DP...
and Lindström quantifier
Lindström quantifier
In mathematical logic, a Lindström quantifier is a generalized polyadic quantifier. They are a generalization of first-order quantifiers, such as the existential quantifier, the universal quantifier, and the counting quantifiers.They were introduced by Per Lindström in 1966.-Generalization of...
for further details.
Mathematics
Consider the following statement:- 1·2 = 1 + 1, and 2·2 = 2 + 2, and 3 · 2 = 3 + 3, ...., and n · 2 = n + n, etc.
This has the appearance of an infinite conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of propositions. From the point of view of formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s this is immediately a problem, since syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
rules are expected to generate finite objects. The example above is fortunate in that there is a procedure
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to generate all the conjuncts. However, if an assertion were to be made about every irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, there would be no way to enumerate all the conjuncts, since irrationals cannot be enumerated. A succinct formulation which avoids these problems uses universal quantification:
- For any natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, n·2 = n + n.
A similar analysis applies to the disjunction,
- 1 is equal to 5 + 5, or 2 is equal to 5 + 5, or 3 is equal to 5 + 5, ... , or n is equal to 5 + 5, etc.
which can be rephrased using existential quantification:
- For some natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, n is equal to 5 + 5.
It is possible to devise abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
s whose models
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
include formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s with quantification, but progress has been slow and interest in such algebra has been limited. Three approaches have been devised to date:
- Relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
, invented by DeMorgan, and developed by Charles Sanders Peirce, Ernst SchröderErnst SchröderErnst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
, Tarski, and Tarski's students. Relation algebra cannot represent any formula with quantifiers nested more than three deep. Surprisingly, the modelsModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of relation algebra include the axiomatic set theory ZFC and Peano arithmetic; - Cylindric algebraCylindric algebraThe notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional...
, devised by Tarski, HenkinHenkinHenkin is a Jewish last name and may refer to the following people:*Leon Henkin, logician and mathematician**Henkin quantifier, a concept he pioneered*Dr. William A...
, and others; - The polyadic algebraPolyadic algebraPolyadic algebras are algebraic structures introduced by Paul Halmos. They are related to first-order logic in a way analogous to the relationship between Boolean algebras and propositional logic .There are other ways to relate first-order logic to algebra, including Tarski's cylindric algebras...
of Paul HalmosPaul HalmosPaul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
.
Notation
The traditional symbol for the universal quantifier is "∀", an inverted letter "AA
A is the first letter and a vowel in the basic modern Latin alphabet. It is similar to the Ancient Greek letter Alpha, from which it derives.- Origins :...
", which stands for the word "all"; in other schools, a
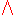is used instead. The corresponding symbol for the existential quantifier is "∃", a rotated letter "EE
E is the fifth letter and a vowel in the basic modern Latin alphabet. It is the most commonly used letter in the Czech, Danish, Dutch, English, French, German, Hungarian, Latin, Norwegian, Spanish, and Swedish languages.-History:...
", which stands for the word "exists". Other schools use the symbol
instead.Correspondingly, quantified expressions are constructed as follows,
for a formula P. Variant notations include, for set X and set members x:
All of these variations also apply to universal quantification.
Other variations for the universal quantifier are
Some versions of the notation explicitly mention the range of quantification. The range of quantification must always be specified; for a given mathematical theory, this can be done in several ways:
- Assume a fixed domain of discourse for every quantification, as is done in Zermelo–Fraenkel set theoryZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, - Fix several domains of discourse in advance and require that each variable have a declared domain, which is the type of that variable. This is analogous to the situation in statically typedType systemA type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
computer programmingComputer programmingComputer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
languages, where variables have declared types. - Mention explicitly the range of quantification, perhaps using a symbol for the set of all objects in that domain or the type of the objects in that domain.
One can use any variable as a quantified variable in place of any other, under certain restrictions in which variable capture does not occur. Even if the notation uses typed variables, variables of that type may be used.
Informally or in natural language, the "∀x" or "∃x" might appear after or in the middle of P(x). Formally, however, the phrase that introduces the dummy variable is placed in front.
Mathematical formulas mix symbolic expressions for quantifiers, with natural language quantifiers such as
- For any natural number x, ....
- There exists an x such that ....
- For at least one x.
Keywords for uniqueness quantification
Uniqueness quantification
In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
include:
- For exactly one natural number x, ....
- There is one and only one x such that ....
Further, x may be replaced by a pronoun
Pronoun
In linguistics and grammar, a pronoun is a pro-form that substitutes for a noun , such as, in English, the words it and he...
. For example,
- For any natural number, its product with 2 equals to its sum with itself
- Some natural number is prime.
Equivalent Expressions
If X is a domain of x and P(x) is a predicate dependent on x, then the universal proposition is expressed in Boolean algebraBoolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
terms as
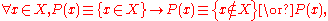
which equivalently reads "if x is in X, then P(x) is true." If x is not in X, then P(x) is indeterminate. Note that the truth of the expression requires only that x be in X, so it can be any x in X, independent of P(x), whereas the falsity of the expression, or the truth of
additionally requires that x be such that P(x) evaluates to false; this is the reason behind calling x a "bound variable." This last expression can thus be read as "for some x in X, P(x) is false," or "there exists an x in X such that P(x) is false." So, we now have the equivalent Boolean expression for the existential proposition:
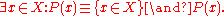
Thus, together with negation, only one of either the universal or existential quantifier is needed to perform both tasks:
which shows that to disprove a "for all x" proposition, one needs no more than to find an x for which the predicate is false. Similarly,
to disprove a "there exists an x" proposition, one needs to show that the predicate is false for all x.
Nesting
Consider the following statement:- For any natural number
, there is a natural number 
such that 
.
This is clearly true; it just asserts that every natural number has a square. The meaning of the assertion in which the quantifiers are turned around is different:
- There is a natural number
such that for any natural number 
, 
.
This is clearly false; it asserts that there is a single natural number s that is at once the square of every natural number. This is because the syntax directs that any newly introduced variable cannot be a function of subsequently introduced variables.
This illustrates that the order of quantifiers is critical to meaning.
A less trivial example is the important concept of uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
from analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, which differs from the more familiar concept of pointwise continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
only by an exchange in the positions of two quantifiers.
To illustrate this, let f be a real-valued function on R.
- A: Pointwise continuity of
on R:
interchanging the universal quantifiers over the braces, this is the same as
- A': Pointwise continuity of f on R:
Thus, it is implied that the particular value chosen for δ can only be a function of ε and x, the variables that precede it; whereas in
- B: Uniform continuity of f on R:
by interchanging the existential and universal quantifiers over the braces in A', δ is asserted to be independent of x.
Ambiguity is avoided with the quantifiers in front:
A:
B: C – unambiguous- there is an A such that
B: C – unambiguous - there is an A such that for all B, C – unambiguous, provided that the separation between B and C is clear
- there is an A such that C for all B – it is often clear that what is meant is
-
- there is an A such that (C for all B)
- but it could be interpreted as
- (there is an A such that C) for all B
- there is an A such that C
B – suggests more strongly that the first is meant; this may be reinforced by the layout, for example by putting "C 
B" on a new line.
- there is an A such that C
- (there is an A such that C) for all B
Range of quantification
Every quantification involves one specific variable and a domain of discourse or range of quantification of that variable. The range of quantification specifies the set of values that the variable takes. In the examples above, the range of quantification is the set of natural numbers. Specification of the range of quantification allows us to express the difference between, asserting that a predicate holds for some natural number or for some real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Expository conventions often reserve some variable names such as "n" for natural numbers and "x" for real numbers, although relying exclusively on naming conventions cannot work in general since ranges of variables can change in the course of a mathematical argument.
A more natural way to restrict the domain of discourse uses guarded quantification. For example, the guarded quantification
- For some natural number n, n is even and n is prime
means
- For some even number n, n is prime.
In some mathematical theories a single domain of
discourse fixed in advance is assumed. For example, in Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, variables range over all sets. In this case, guarded quantifiers can be used to mimic a smaller range of quantification. Thus in the example
above to express
- For any natural number n, n·2 = n + n
in Zermelo–Fraenkel set theory, it can be said
- For any n, if n belongs to N, then n·2 = n + n,
where N is the set of all natural numbers.
Formal semantics
Mathematical Semantics is the application of mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
to study the meaning of expressions in a formal language. It has three elements: A mathematical specification of a class of objects via syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
, a mathematical specification of various semantic domains and the relation between the two, which is usually expressed as a function from syntactic objects to semantic ones. This article only addresses the issue of how quantifier elements are interpreted.
Given a model theoretical
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
logical framework, the syntax of a formula can be given by a syntax tree. Quantifiers have scope and a variable x is free if it is not within the scope of a quantification for that variable. Thus in
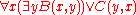
the occurrence of both x and y in C(y,x) is free.
An interpretation for first-order predicate calculus assumes as given
a domain of individuals X. A formula A whose free variables
are x1, ..., xn is interpreted as a
boolean-valued function F(v1, ...,
vn) of n arguments, where each argument ranges
over the domain X. Boolean-valued means that the function assumes one of the values T (interpreted as truth) or F (interpreted as falsehood). The interpretation of the formula
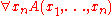
is the function G of n-1 arguments such that G(v1, ...,vn-1) = T if and only if F(v1, ..., vn-1, w) = T for every w in X. If F(v1, ..., vn-1, w) = F for at least one value of w, then G(v1, ...,vn-1) = F. Similarly the interpretation of the formula
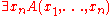
is the function H of n-1 arguments such that H(v1, ...,vn-1) = T if and only if F(v1, ...,vn-1, w) = T for at least one w and H(v1, ..., vn-1) = F otherwise.
The semantics for uniqueness quantification
Uniqueness quantification
In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
requires first-order predicate calculus with equality. This means there is given a distinguished two-placed predicate "="; the semantics is also modified accordingly so that "=" is always interpreted as the two-place equality relation on X. The interpretation of
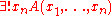
then is the function of n-1 arguments, which is the logical and of the interpretations of
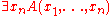
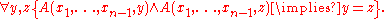
Paucal, multal and other degree quantifiers
None of the quantifiers previously discussed apply to a quantification such as- There are many integers n < 100, such that n is divisible by 2 or 3 or 5.
One possible interpretation mechanism can be obtained as follows: Suppose that in addition to a semantic domain X, we have given a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P defined on X and cutoff numbers 0 < a ≤ b ≤ 1. If A is a formula with free variables x1,...,xn whose interpretation is
the function F of variables v1,...,vn
then the interpretation of
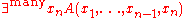
is the function of v1,...,vn-1 which is T if and only if
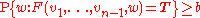
and F otherwise. Similarly, the interpretation of
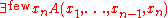
is the function of v1,...,vn-1 which is F if and only if
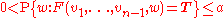
and T otherwise. See Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
for more discussion of the measurability of the interpretation functions.
Other quantifiers
A few other quantifiers have been proposed over time. In particular, the solution quantifier, noted § (section signSection sign
The section sign , also called the "double S", "sectional symbol" or signum sectiōnis, is a typographical character used mainly to refer to a particular section of a document, such as a legal code. It is frequently used along with the pilcrow , or paragraph sign...
) and read "those". For example:
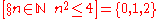
is read "those n in N such that n2 ≤ 4 are in {0,1,2}." The same construct is expressible in set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
:
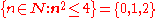
History
Term logicTerm logic
In philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
treats quantification in a manner that is closer to natural language, and also less suited to formal analysis. Aristotelian logic treated All, Some and No in the 1st century BC, in an account also touching on the alethic modalities.
Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, in his 1879 Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
, was the first to employ a quantifier to bind a variable ranging over a domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
and appearing in predicates. He would universally quantify a variable (or relation) by writing the variable over a dimple in an otherwise straight line appearing in his diagrammatic formulas. Frege did not devise an explicit notation for existential quantification, instead employing his equivalent of ~∀x~, or contraposition
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
. Frege's treatment of quantification went largely unremarked until Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
's 1903 Principles of Mathematics.
In work that culminated in Peirce (1885), Charles Sanders Peirce and his student Oscar Howard Mitchell independently invented universal and existential quantifiers, and bound variables. Peirce and Mitchell wrote Πx and Σx where we now write ∀x and ∃x. Peirce's notation can be found in the writings of Ernst Schröder
Ernst Schröder
Ernst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
, Leopold Loewenheim, Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
, and Polish logicians into the 1950s. Most notably, it is the notation of Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
's landmark 1930 paper on the completeness
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, and 1931 paper on the incompleteness of Peano arithmetic.
Peirce's approach to quantification also influenced William Ernest Johnson
William Ernest Johnson
William Ernest Johnson was a British logician mainly remembered for his Logic , in 3 volumes....
and Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
, who invented yet another notation, namely (x) for the universal quantification of x and (in 1897) ∃x for the existential quantification of x. Hence for decades, the canonical notation in philosophy and mathematical logic was (x)P to express "all individuals in the domain of discourse have the property P," and "(∃x)P" for "there exists at least one individual in the domain of discourse having the property P." Peano, who was much better known than Peirce, in effect diffused the latter's thinking throughout Europe. Peano's notation was adopted by the Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
of Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
and Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
, Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
, and Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
. In 1935, Gentzen introduced the ∀ symbol, by analogy with Peano's ∃ symbol. ∀ did not become canonical until the 1960s.
Around 1895, Peirce began developing his existential graph
Existential graph
An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914.-The graphs:...
s, whose variables can be seen as tacitly quantified. Whether the shallowest instance of a variable is even or odd determines whether that variable's quantification is universal or existential. (Shallowness is the contrary of depth, which is determined by the nesting of negations.) Peirce's graphical logic has attracted some attention in recent years by those researching heterogeneous reasoning and diagrammatic inference
Logical graph
A logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
.
Natural science
Some measure of the undisputed general importance of quantification in the natural scienceNatural science
The natural sciences are branches of science that seek to elucidate the rules that govern the natural world by using empirical and scientific methods...
s can be gleaned from the following comments: "these are mere facts, but they are quantitative facts and the basis of science." It seems to be held as universally true that "the foundation of quantification is measurement." There is little doubt that "quantification provided a basis for the objectivity of science." In ancient times, "musicians and artists...rejected quantification, but merchants, by definition, quantified their affairs, in order to survive, made them visible on parchment and paper." Any reasonable "comparison between Aristotle and Galileo shows clearly that there can be no unique lawfulness discovered without detailed quantification." Even today, "universities use imperfect instruments called 'exams' to indirectly quantify something they call knowledge." This meaning of quantification comes under the heading of pragmatics
Pragmatics
Pragmatics is a subfield of linguistics which studies the ways in which context contributes to meaning. Pragmatics encompasses speech act theory, conversational implicature, talk in interaction and other approaches to language behavior in philosophy, sociology, and linguistics. It studies how the...
.
In some instances in the natural sciences a seemingly intangible concept may be quantified by creating a scale—for example, a pain scale
Pain scale
A pain scale measures a patient's pain intensity or other features. Pain scales are based on self-report, observational , or physiological data. Self-report is considered primary and should be obtained if possible. Pain scales are available for neonates, infants, children, adolescents, adults,...
in medical research, or a discomfort scale at the intersection of meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
and human physiology
Human physiology
Human physiology is the science of the mechanical, physical, bioelectrical, and biochemical functions of humans in good health, their organs, and the cells of which they are composed. Physiology focuses principally at the level of organs and systems...
such as the heat index
Heat index
The heat index is an index that combines air temperature and relative humidity in an attempt to determine the human-perceived equivalent temperature — how hot it feels, termed the felt air temperature. The human body normally cools itself by perspiration, or sweating, which evaporates and carries...
measuring the combined perceived effect of heat and humidity
Humidity
Humidity is a term for the amount of water vapor in the air, and can refer to any one of several measurements of humidity. Formally, humid air is not "moist air" but a mixture of water vapor and other constituents of air, and humidity is defined in terms of the water content of this mixture,...
, or the wind chill factor measuring the combined perceived effects of cold and wind.
Social sciences
In the social sciencesSocial sciences
Social science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
, quantification is an integral part of economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
. Both disciplines gather data—economics by empirical observation and psychology by experimentation, and both use statistical techniques
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
such as regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
to draw conclusions from it.
In some instances a seemingly intangible property may be quantified by asking subjects to rate something on a scale
Scale (social sciences)
In the social sciences, scaling is the process of measuring or ordering entities with respect to quantitative attributes or traits. For example, a scaling technique might involve estimating individuals' levels of extraversion, or the perceived quality of products...
—for example, a happiness scale or a quality of life scale
Self-Perceived Quality of Life Scale
Self-perceived quality-of-life scale is a psychological assessment instrument which is based on a comprehensive theory of the Self-Perceived Quality of Life and provides a multi-faceted measurement of health-related and non-health-related aspects of well-being...
—or by the construction of a scale by the researcher, as with the index of economic freedom
Index of Economic Freedom
The Index of Economic Freedom is a series of 10 economic measurements created by The Heritage Foundation and The Wall Street Journal. Its stated objective is to measure the degree of economic freedom in the world's nations....
. In other cases, an unobservable variable may be quantified by replacing it with a proxy variable
Proxy (statistics)
In statistics, a proxy variable is something that is probably not in itself of any great interest, but from which a variable of interest can be obtained...
with which it is highly correlated—for example, per capita gross domestic product
Gross domestic product
Gross domestic product refers to the market value of all final goods and services produced within a country in a given period. GDP per capita is often considered an indicator of a country's standard of living....
is often used as a proxy for standard of living
Standard of living
Standard of living is generally measured by standards such as real income per person and poverty rate. Other measures such as access and quality of health care, income growth inequality and educational standards are also used. Examples are access to certain goods , or measures of health such as...
or quality of life
Quality of life
The term quality of life is used to evaluate the general well-being of individuals and societies. The term is used in a wide range of contexts, including the fields of international development, healthcare, and politics. Quality of life should not be confused with the concept of standard of...
.
Frequently in the use of regression, the presence or absence of a trait is quantified by employing a dummy variable, which takes on the value 1 in the presence of the trait or the value 0 in the absence of the trait.
Quantitative linguistics
Quantitative linguistics
Quantitative linguistics is a sub-discipline of general linguistics and, more specifically, of mathematical linguistics. Quantitative Linguistics deals with language learning, language change, and application as well as structure of natural languages...
is an area of linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
that relies on quantification. For example, indices of grammaticalization of morpheme
Morpheme
In linguistics, a morpheme is the smallest semantically meaningful unit in a language. The field of study dedicated to morphemes is called morphology. A morpheme is not identical to a word, and the principal difference between the two is that a morpheme may or may not stand alone, whereas a word,...
s, such as phonological
Phonology
Phonology is, broadly speaking, the subdiscipline of linguistics concerned with the sounds of language. That is, it is the systematic use of sound to encode meaning in any spoken human language, or the field of linguistics studying this use...
shortness, dependence on surroundings, and fusion with the verb, have been developed and found to be significantly correlated across languages with stage of evolution of function of the morpheme.
Hard versus soft science
The ease of quantification is one of the features used to distinguish hard and soft scienceHard and soft science
Hard science and soft science are colloquial terms often used when comparing scientific fields of academic research or scholarship, with hard meaning perceived as being more scientific, rigorous, or accurate...
s from each other. Hard sciences are often considered to be more scientific, rigorous, or accurate. In some social sciences
Social sciences
Social science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
such as sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, specific accurate data are difficult to obtain, either because laboratory conditions are not present or because the issues involved are conceptual but not directly quantifiable.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- "Classical Logic -- by Stewart Shapiro. Covers syntax, model theory, and metatheory for first order logic in the natural deduction style.
- "Generalized quantifiers" -- by Dag Westerståhl.
- Peters, Stanley; Westerståhl, Dag (2002). "Quantifiers."