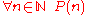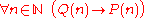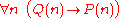Universal quantification
Encyclopedia
In predicate logic
, universal quantification formalizes the notion that something (a logical predicate) is true for everything, or every relevant thing.
The resulting statement is a universally quantified statement, and we have universally quantified over the predicate.
In symbolic logic
, the universal quantifier (typically
, ∀, a turned A
) is the symbol used to denote universal quantification, and is often informally read as "given any" or "for all". Universal quantification is distinct from existential quantification
("there exists"), which asserts that the property or relation holds for at least one member of the domain.
Quantification in general is covered in the article on quantification
. Symbols are encoded .
This would seem to be a logical conjunction
because of the repeated use of "and." However, the "etc." cannot be interpreted as a conjunction in formal logic
. Instead, the statement must be rephrased:
This is a single statement using universal quantification.
This statement can be said to be more precise than the original one. While the "etc." informally includes natural number
s, and nothing more, this was not rigorously given. In the universal quantification, on the other hand, the natural numbers are mentioned explicitly.
This particular example is true, because any natural number could be substituted for n and the statement "2·n = n + n" would be true. In contrast,
is false, because if n is substituted with, for instance, 1, the statement "2·1 > 2 + 1" is false. It is immaterial that "2·n > 2 + n" is true for most natural numbers n: even the existence of a single counterexample
is enough to prove the universal quantification false.
On the other hand,
for all composite number
s n, 2·n > 2 + n
is true, because none of the counterexamples are composite numbers. This indicates the importance of the domain of discourse
, which specifies which values n can take.Further information on using domains of discourse with quantified statements can be found in the Quantification
article. In particular, note that if the domain of discourse is restricted to consist only of those objects that satisfy a certain predicate, then for universal quantification this requires a logical conditional. For example,
is logically equivalent to
Here the "if ... then" construction indicates the logical conditional.
, the universal quantifier symbol
(a inverted
"A
" in a sans-serif
font, Unicode 0x2200) is used to indicate universal quantification.
For example, if P(n) is the predicate "2·n > 2 + n" and N is the set of natural numbers, then:
is the (false) statement:
Similarly, if Q(n) is the predicate "n is composite", then
is the (true) statement:
and since "n is composite" implies that n must already be a natural number, we can shorten this statement to the equivalent:
Several variations in the notation for quantification (which apply to all forms) can be found in the quantification
article. There is a special notation used only for universal quantification, which is given:
The parentheses indicate universal quantification by default.
is a statement; thus, like statements, quantified functions can be negated. The notation most mathematicians and logicians utilize to denote negation is:
. However, some (such as Douglas Hofstadter
) use the tilde
(~).
For example, if P(x) is the propositional function "x is married", then, for a Universe of Discourse X of all living human beings, the universal quantification
is given:
It can be seen that this is irrevocably false. Truthfully, it is stated that
or, symbolically: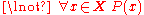
.
If the statement is not true for every element of the Universe of Discourse, then, presuming the universe of discourse is non-empty, there must be at least one element for which the statement is false. That is, the negation of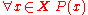
is logically equivalent to "There exists a living person x such that he is not married", or: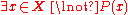
Generally, then, the negation of a propositional function's universal quantification is an existential quantification
of that propositional function's negation; symbolically,
It is erroneous to state "all persons are not married" (i.e. "there exists no person who is married") when it is meant that "not all persons are married" (i.e. "there exists a person who is not married"):
s ∧
, ∨
, →
, and
, as long as the other operand is not affected; that is:
Conversely, for the logical connectives ↑
, ↓
,
, and ←
, the quantifiers flip:
is a rule justifying a logical step from hypothesis to conclusion. There are several rules of inference which utilize the universal quantifier.
Universal instantiation
concludes that, if the propositional function is known to be universally true, then it must be true for any arbitrary element of the Universe of Discourse. Symbolically, this is represented as
where c is a completely arbitrary element of the Universe of Discourse.
Universal generalization
concludes the propositional function must be universally true if it is true for any arbitrary element of the Universe of Discourse. Symbolically, for an arbitrary c,
The element c must be completely arbitrary; else, the logic does not follow: if c is not arbitrary, and is instead a specific element of the Universe of Discourse, then P(c) only implies an existential quantification of the propositional function.
By convention, the formula
is always true, regardless of the formula P(x); see vacuous truth
.
is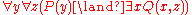
.
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
, universal quantification formalizes the notion that something (a logical predicate) is true for everything, or every relevant thing.
The resulting statement is a universally quantified statement, and we have universally quantified over the predicate.
In symbolic logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, the universal quantifier (typically
, ∀, a turned ATurned a
Turned A is a letter of the Latin alphabet based upon the letter A. It is not, nor has it ever been, used in any natural languages as a letter in its own right....
) is the symbol used to denote universal quantification, and is often informally read as "given any" or "for all". Universal quantification is distinct from existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
("there exists"), which asserts that the property or relation holds for at least one member of the domain.
Quantification in general is covered in the article on quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
. Symbols are encoded .
Basics
Suppose it is given that2·0 = 0 + 0, and 2·1 = 1 + 1, and 2·2 = 2 + 2, etc.
This would seem to be a logical conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
because of the repeated use of "and." However, the "etc." cannot be interpreted as a conjunction in formal logic
Formal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
. Instead, the statement must be rephrased:
For all natural numbers n, 2·n = n + n.
This is a single statement using universal quantification.
This statement can be said to be more precise than the original one. While the "etc." informally includes natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, and nothing more, this was not rigorously given. In the universal quantification, on the other hand, the natural numbers are mentioned explicitly.
This particular example is true, because any natural number could be substituted for n and the statement "2·n = n + n" would be true. In contrast,
For all natural numbers n, 2·n > 2 + n
is false, because if n is substituted with, for instance, 1, the statement "2·1 > 2 + 1" is false. It is immaterial that "2·n > 2 + n" is true for most natural numbers n: even the existence of a single counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
is enough to prove the universal quantification false.
On the other hand,
for all composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s n, 2·n > 2 + n
is true, because none of the counterexamples are composite numbers. This indicates the importance of the domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
, which specifies which values n can take.Further information on using domains of discourse with quantified statements can be found in the Quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
article. In particular, note that if the domain of discourse is restricted to consist only of those objects that satisfy a certain predicate, then for universal quantification this requires a logical conditional. For example,
For all composite numbers n, 2·n > 2 + n
is logically equivalent to
For all natural numbers n, if n is composite, then 2·n > 2 + n.
Here the "if ... then" construction indicates the logical conditional.
Notation
In symbolic logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, the universal quantifier symbol
(a invertedTurned a
Turned A is a letter of the Latin alphabet based upon the letter A. It is not, nor has it ever been, used in any natural languages as a letter in its own right....
"A
A
A is the first letter and a vowel in the basic modern Latin alphabet. It is similar to the Ancient Greek letter Alpha, from which it derives.- Origins :...
" in a sans-serif
Sans-serif
In typography, a sans-serif, sans serif or san serif typeface is one that does not have the small projecting features called "serifs" at the end of strokes. The term comes from the French word sans, meaning "without"....
font, Unicode 0x2200) is used to indicate universal quantification.
For example, if P(n) is the predicate "2·n > 2 + n" and N is the set of natural numbers, then:
is the (false) statement:
For all natural numbers n, 2·n > 2 + n.
Similarly, if Q(n) is the predicate "n is composite", then
is the (true) statement:
For all natural numbers n, if n is composite, then 2·n > 2 + n
and since "n is composite" implies that n must already be a natural number, we can shorten this statement to the equivalent:
For all composite numbers n, 2·n > 2 + n.
Several variations in the notation for quantification (which apply to all forms) can be found in the quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
article. There is a special notation used only for universal quantification, which is given:
The parentheses indicate universal quantification by default.
Negation
Note that a quantified propositional functionPropositional function
A propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
is a statement; thus, like statements, quantified functions can be negated. The notation most mathematicians and logicians utilize to denote negation is:
. However, some (such as Douglas HofstadterDouglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
) use the tilde
Tilde
The tilde is a grapheme with several uses. The name of the character comes from Portuguese and Spanish, from the Latin titulus meaning "title" or "superscription", though the term "tilde" has evolved and now has a different meaning in linguistics....
(~).
For example, if P(x) is the propositional function "x is married", then, for a Universe of Discourse X of all living human beings, the universal quantification
Given any living person x, that person is married
is given:
It can be seen that this is irrevocably false. Truthfully, it is stated that
It is not the case that, given any living person x, that person is married
or, symbolically:
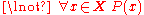.If the statement is not true for every element of the Universe of Discourse, then, presuming the universe of discourse is non-empty, there must be at least one element for which the statement is false. That is, the negation of
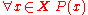is logically equivalent to "There exists a living person x such that he is not married", or: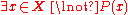Generally, then, the negation of a propositional function's universal quantification is an existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
of that propositional function's negation; symbolically,
It is erroneous to state "all persons are not married" (i.e. "there exists no person who is married") when it is meant that "not all persons are married" (i.e. "there exists a person who is not married"):
Other connectives
The universal (and existential) quantifier moves unchanged across the logical connectiveLogical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s ∧
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, ∨
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
, →
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
, and
, as long as the other operand is not affected; that is:Conversely, for the logical connectives ↑
Sheffer stroke
In Boolean functions and propositional calculus, the Sheffer stroke, named after Henry M. Sheffer, written "|" , "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both"...
, ↓
Logical NOR
In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false...
,
Material nonimplication
Material nonimplication or abjunction is the negation of implication. That is to say that for any two propositions P and Q, if P does not imply Q, then P is the material nonimplication of Q....
, and ←
Converse implication
Converse implication is the converse of implication. That is to say; that for any two propositions P and Q, if Q implies P, then P is the converse implication of Q.It may take the following forms:-Truth table:The truth table of A⊂B-Venn diagram:...
, the quantifiers flip:
Rules of inference
A rule of inferenceRule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
is a rule justifying a logical step from hypothesis to conclusion. There are several rules of inference which utilize the universal quantifier.
Universal instantiation
Universal instantiation
In logic universal instantiation is an inference from a truth about each member of a class of individuals to the truth about a particular individual of that class. It is generally given as a quantification rule for the universal quantifier but it can also be encoded in an axiom...
concludes that, if the propositional function is known to be universally true, then it must be true for any arbitrary element of the Universe of Discourse. Symbolically, this is represented as
where c is a completely arbitrary element of the Universe of Discourse.
Universal generalization
Generalization (logic)
In mathematical logic, generalization is an inference rule of predicate calculus. It states that if \vdash P has been derived, then \vdash \forall x \, P can be derived....
concludes the propositional function must be universally true if it is true for any arbitrary element of the Universe of Discourse. Symbolically, for an arbitrary c,
The element c must be completely arbitrary; else, the logic does not follow: if c is not arbitrary, and is instead a specific element of the Universe of Discourse, then P(c) only implies an existential quantification of the propositional function.
The empty set
By convention, the formula
is always true, regardless of the formula P(x); see vacuous truthVacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
.
Universal closure
The universal closure of a formula φ is the formula with no free variables obtained by adding a universal quantifier for every free variable in φ. For example, the universal closure ofis
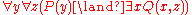.See also
- Existential quantificationExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
- Quantifiers
- First-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...